Пересечение треугольника и пятиугольника

Видео:Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Ваш ответ

Видео:Построение пятиугольника циркулемСкачать

решение вопроса

Видео:Пересечение плоскостей (треугольника и четырёхугольника)Скачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,036
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Задание 51. Как начертить ЛИНИЮ ПЕРЕСЕЧЕНИЯ ПРИЗМ.Скачать

Как начертить два треугольника так, чтоб их пересечением были шестиугольник и пятиугольник?

Математика | 10 — 11 классы

Как начертить два треугольника так, чтоб их пересечением были шестиугольник и пятиугольник?

Вот так примерно один треугольник на другой нарисовать.

Видео:Пересечение биссектрис треугольника в одной точке, Геометрия 7 классСкачать

Как начертить два треугольника чтобы их пересечением был шестиугольник?

Как начертить два треугольника чтобы их пересечением был шестиугольник.

Видео:Построение недостающей проекции плоскости. Принадлежность прямой к плоскостиСкачать

Начерти пятиугольник АВСDЕ и проведи прямую l так чтобы она разбила пятиугольник : а) на треугольник и шестиугольник б) на треугольник и пятиугольник : в) на четырехугольник и пятиугольник : г) на два?

Начерти пятиугольник АВСDЕ и проведи прямую l так чтобы она разбила пятиугольник : а) на треугольник и шестиугольник б) на треугольник и пятиугольник : в) на четырехугольник и пятиугольник : г) на два четырехугольника.

Видео:Построение линии пересечения поверхности пирамиды с проецирующей плоскостьюСкачать

Как разделить пятиугольник на треугольник и шестиугольник?

Как разделить пятиугольник на треугольник и шестиугольник.

Видео:Линия пересечения плоскостейСкачать

Начертите 2 треугольника так, чтобы их общей частью был : 1) треугольник : 2) четырехугольник : 3) пятиугольник : 4) шестиугольник?

Начертите 2 треугольника так, чтобы их общей частью был : 1) треугольник : 2) четырехугольник : 3) пятиугольник : 4) шестиугольник.

Видео:Regular Pentagon Inscribed in a Circle 240pxСкачать

Начертите 2 треугольника так, чтобы их пересечение было : а : точкой, б : треугольник, в : пятиугольник?

Начертите 2 треугольника так, чтобы их пересечение было : а : точкой, б : треугольник, в : пятиугольник.

Видео:Комплексный чертеж усеченной 5-гранной пирамидыСкачать

Начерти два треугольника так чтобы их пересечение м были : шестиугольник, пятиугольник, четырехугольник?

Начерти два треугольника так чтобы их пересечение м были : шестиугольник, пятиугольник, четырехугольник.

Видео:Золотое сечение и правильный пятиугольникСкачать

Как разделить отрезком пятиугольник на : 1 — треугольник и шестиугольник, 2 — на треугольник и пятиугольник?

Как разделить отрезком пятиугольник на : 1 — треугольник и шестиугольник, 2 — на треугольник и пятиугольник.

Видео:ЗАДАЧА ПРО ПЯТИУГОЛЬНИКСкачать

Начерти два треугольника так, чтобы их общей частью был 1) треугольник 2) четырёхугольгик 3) пятиугольник 4)шестиугольник?

Начерти два треугольника так, чтобы их общей частью был 1) треугольник 2) четырёхугольгик 3) пятиугольник 4)шестиугольник.

Видео:Знаете, как найти сумму углов пятиугольника?Скачать

Начерти пятиугольник ABCDE и проведи прямую l так , чтобы она разбила пятиугольник на треугольник и шестиугольник?

Начерти пятиугольник ABCDE и проведи прямую l так , чтобы она разбила пятиугольник на треугольник и шестиугольник.

Видео:Построить линию пересечения треугольника и параллелограмма.Скачать

Нарисуй два треугольника так что бы их пересечением являлись : 1)отрезок, 2)треугольник, 3)четырехугольник, 4)пятиугольник, 5)шестиугольник,?

Нарисуй два треугольника так что бы их пересечением являлись : 1)отрезок, 2)треугольник, 3)четырехугольник, 4)пятиугольник, 5)шестиугольник,.

Вы перешли к вопросу Как начертить два треугольника так, чтоб их пересечением были шестиугольник и пятиугольник?. Он относится к категории Математика, для 10 — 11 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Математика. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.

Видео:Построить линию пересечения треугольников ABC и DEF. Определить видимость. Вариант 2Скачать

Пересечение треугольника и пятиугольника

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Пошаговое руководство решения задачи №1 — «Нахождение линии пересечения двух плоскостей и определение натуральной величины»

В задаче необходимо найти линию пересечения двух плоскостей и определить натуральную величину одной из них методом плоскопараллельного перемещения.

Для решения такой классической задачи по начертательной геометрии необходимо знать следующий теоретический материал:

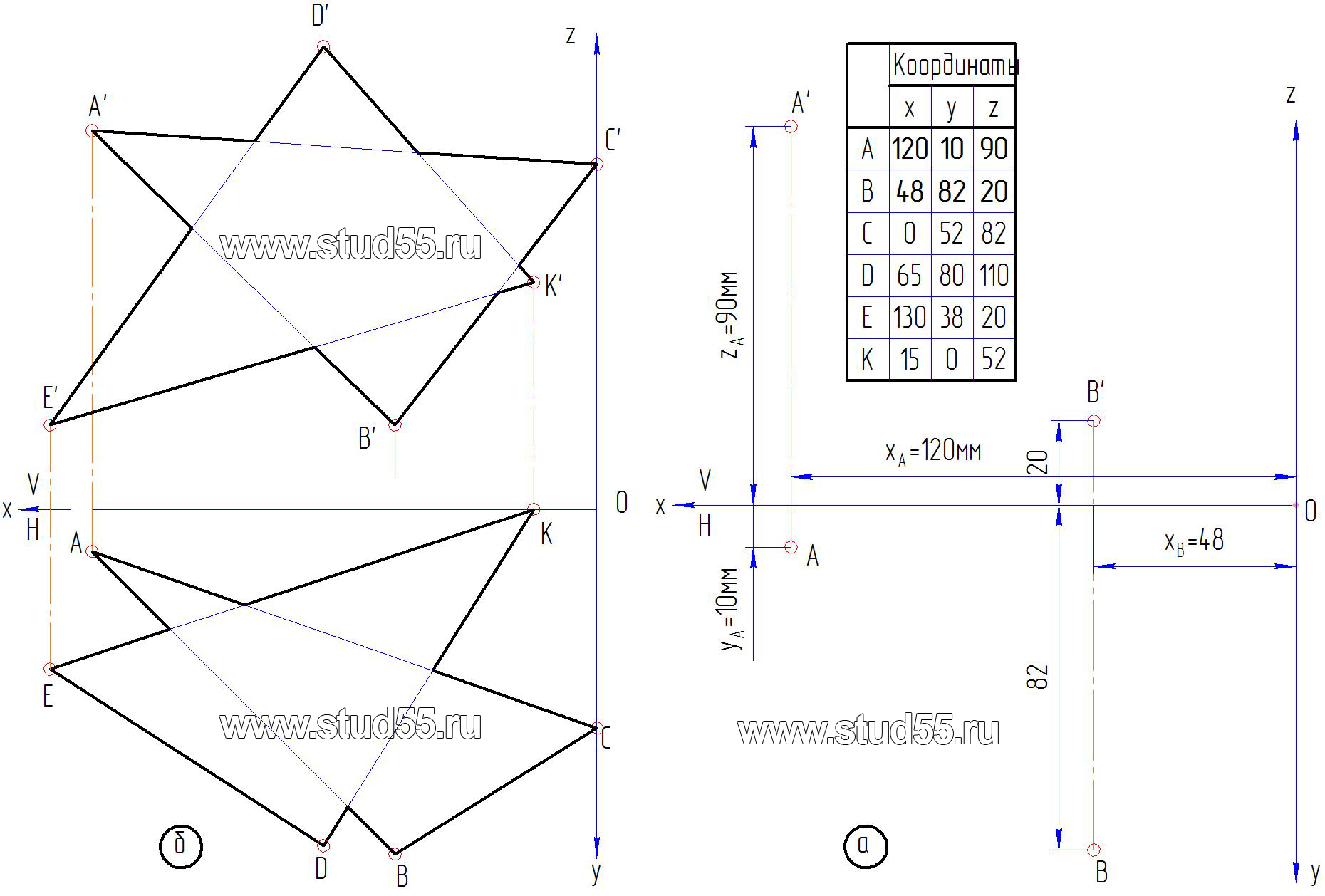
— нанесение проекций точек пространства на комплексный чертеж по заданным координатам;

— способы задания плоскости на комплексном чертеже, плоскости общего и частного положения;

— главные линии плоскости;

— определение точки пересечения прямой линии с плоскостью (нахождение «точки встречи»);

— метод плоскопараллельного перемещения для определения натуральной величины плоской фигуры;

— определение видимости на чертеже прямых линий и плоскостей с помощью конкурирующих точек.

Порядок решения Задачи

1. Согласно варианту Задания по координатам точек наносим на комплексный чертеж две плоскости, заданные в виде треугольников ABC (A’, B’, C’; A, B, C) и DKE (D’, K’, E’; D, K, Е) (рис.1.1).

Рис.1.1

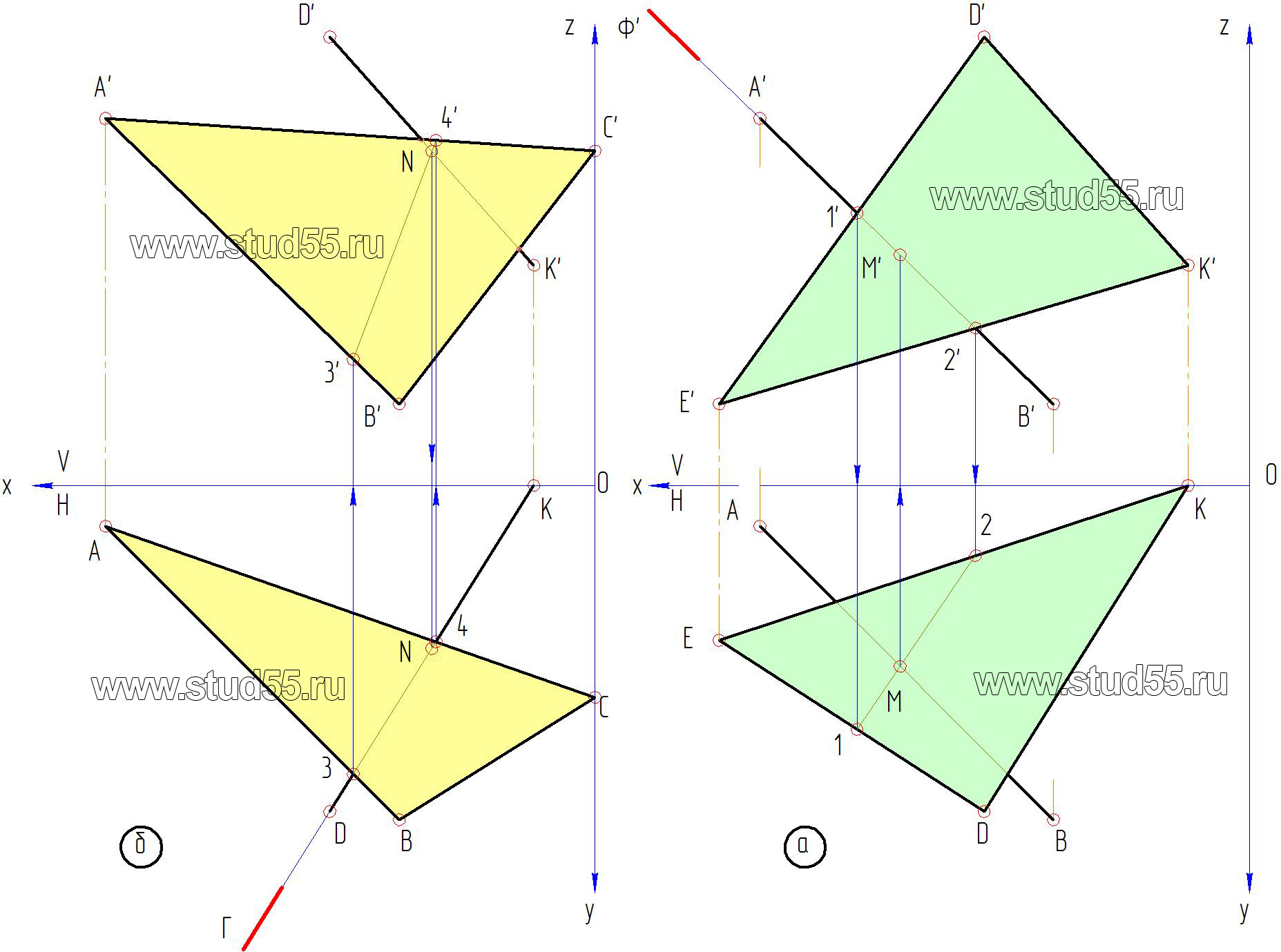
2. Для нахождения линии пересечения воспользуемся методом проецирующей плоскости. Суть его в том, что берется одна сторона (линия) первой плоскости (треугольника) и заключается в проецирующую плоскость. Определяется точка пересечения этой линии с плоскостью второго треугольника. Повторив эту задачу еще раз, но для прямой второго треугольника и плоскости первого треугольника, определим вторую точку пересечения. Так как полученные точки одновременно принадлежат обеим плоскостям, они должны находиться на линии пересечения этих плоскостей. Соединив эти точки прямой, будем иметь искомую линию пересечения плоскостей.

3. Задача решается следующим образом:

а) заключаем в проецирующую плоскость Ф(Ф’) сторону AB(A’B’) первого треугольника во фронтальной плоскости проекций V. Отмечаем точки пересечения проецирующей плоскости со сторонами DK и DE второго треугольника, получая точки 1(1’) и 2 (2’). Переносим их по линиям связи на горизонтальную плоскость проекций H на соответствующие стороны треугольника, точка 1(1) на стороне DE и точка 2(2) на стороне DK.

Рис.1.2

б) соединив проекции точек 1 и 2, будем иметь проекцию проецирующей плоскости Ф. Тогда точка пересечения прямой АВ с плоскостью треугольника DKE определится (согласно правилу) вместе пересечения проекции проецирующей плоскости 1-2 и одноименной проекции прямой AB. Таким образом, получили горизонтальную проекцию первой точки пересечения плоскостей – M, по которой определяем (проецируем по линиям связи) её фронтальную проекцию – M’ на прямой A’B’(рис.1.2.а);

в) аналогичным путем находим вторую точку. Заключаем в проецирующую плоскость Г(Г) сторону второго треугольника DK(DK). Отмечаем точки пересечения проецирующей плоскости со сторонами первого треугольника AC и BC во горизонтальной проекции, получая проекции точек 3 и 4. Проецируем их на соответствующие стороны в фронтальной плоскости, получаем 3’ и 4’. Соединив их прямой, имеем проекцию проецирующей плоскости. Тогда вторая точка пересечения плоскостей будет в месте пересечения линии 3’-4’ со стороной треугольника D’K’, которую заключали в проецирующую плоскость. Таким образом, получили фронтальную проекцию второй точки пересечения – N’, по линии связи находим горизонтальную проекцию – N (рис.1.2.б).

г) соединив полученные точки MN(MN) и (M’N’) на горизонтальной и фронтальной плоскостях, имеем искомую линию пересечения заданных плоскостей.

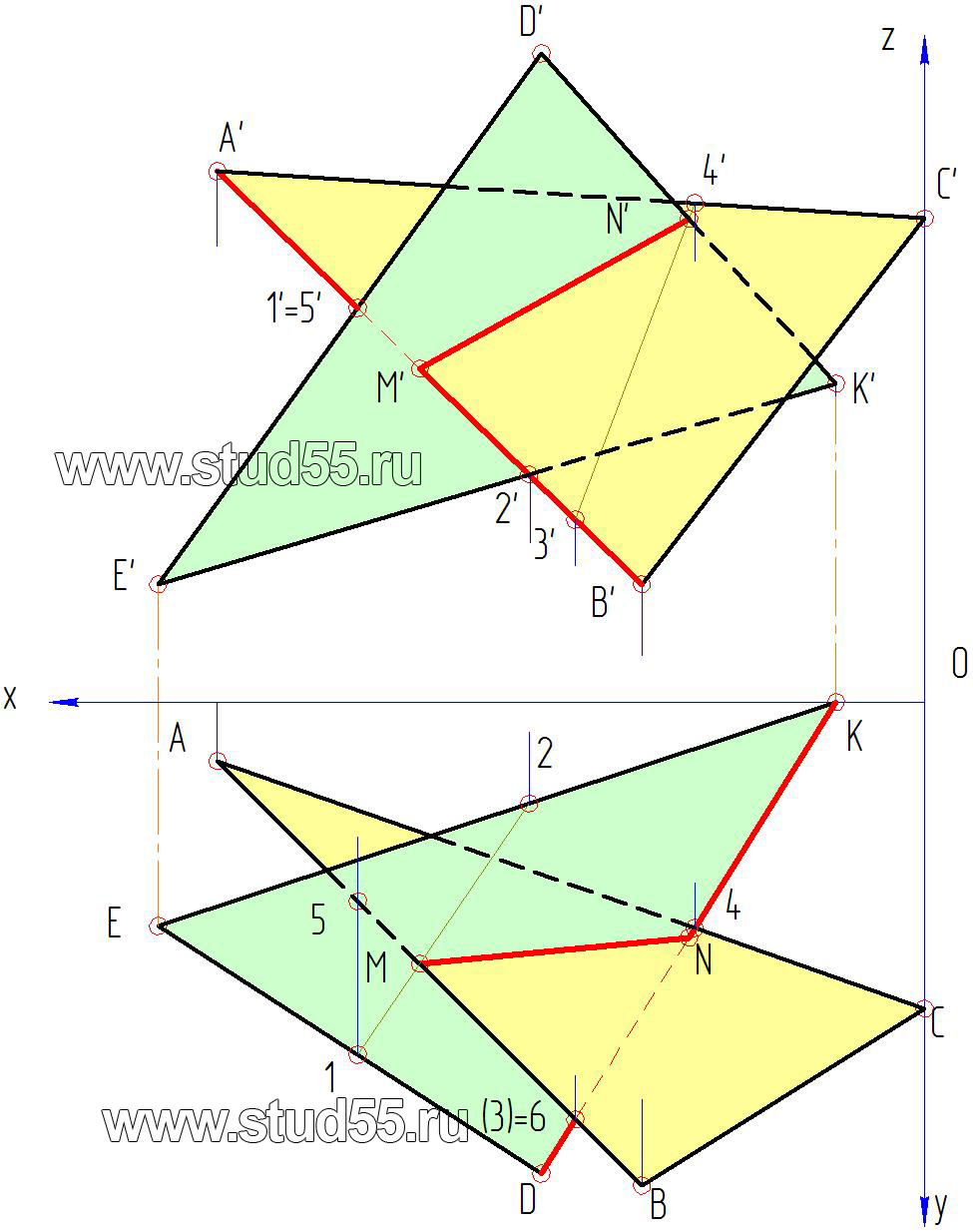
4. С помощью конкурирующих точек определяем видимость плоскостей. Возьмем пару конкурирующих точек, например, 1’=5’ во фронтальной проекции. Спроецируем их на соответствующие стороны в горизонтальную плоскость, получим 1 и 5. Видим, что точка 1, лежащая на стороне DЕ имеет большую координату до оси x, чем точка 5, лежащая на стороне AВ. Следовательно, согласно правилу, большей координаты, точка 1 и сторона треугольника D’Е’ во фронтальной плоскости будут видимые. Таким образом, определяется видимость каждой стороны треугольника в горизонтальной и фронтальной плоскостях. Видимые линии на чертежах проводятся сплошной контурной линией, а не видимые — штриховой линией. Напомним, что в точках пересечения плоскостей (M—N и M’-N’) будет происходить смена видимости.

Рис.1.3

Рис.1.4.

На эпюре дополнительно показано определение видимости в горизонтальной плоскости с использованием конкурирующих точек 3 и 6 на прямых DK и АВ.

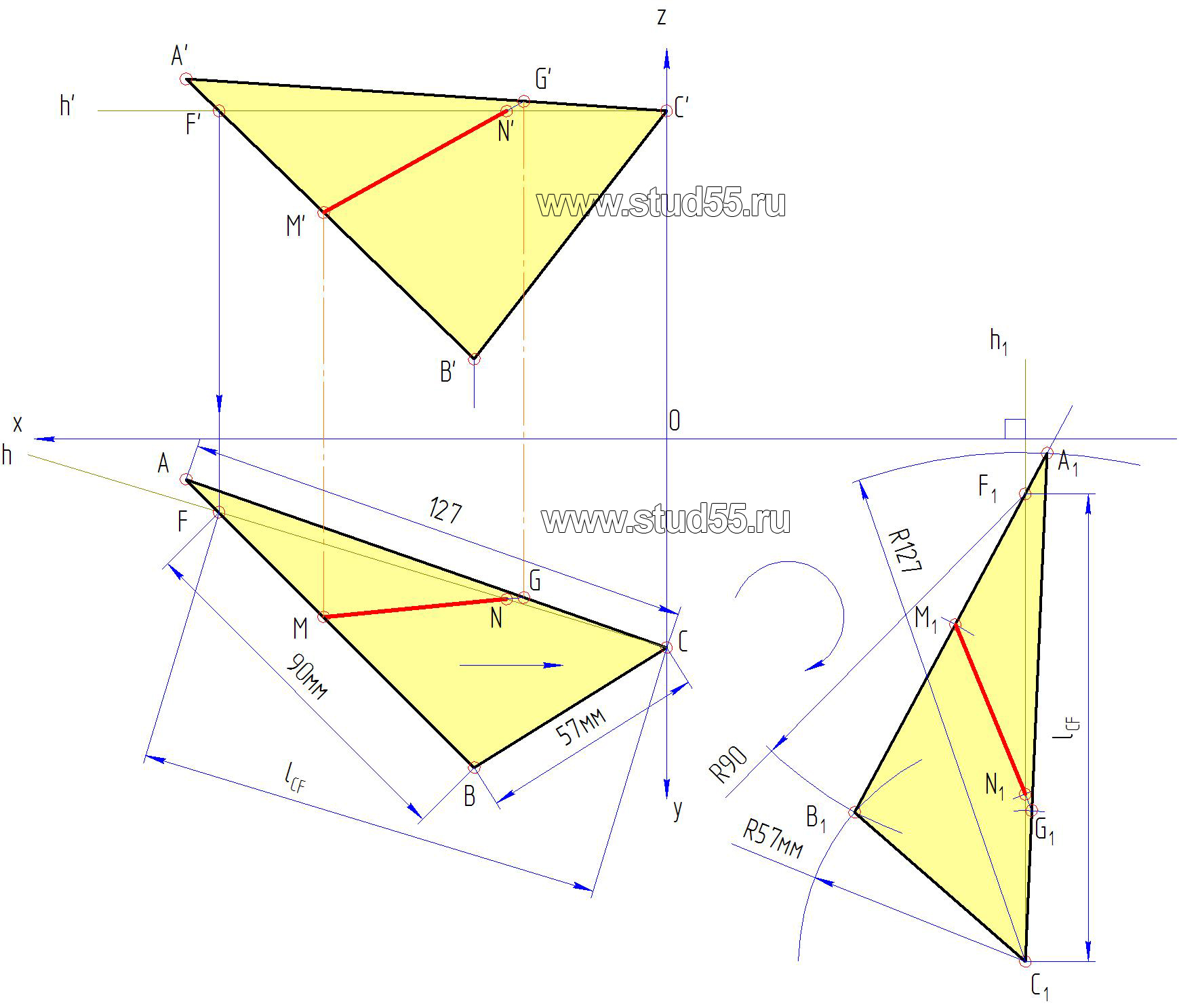
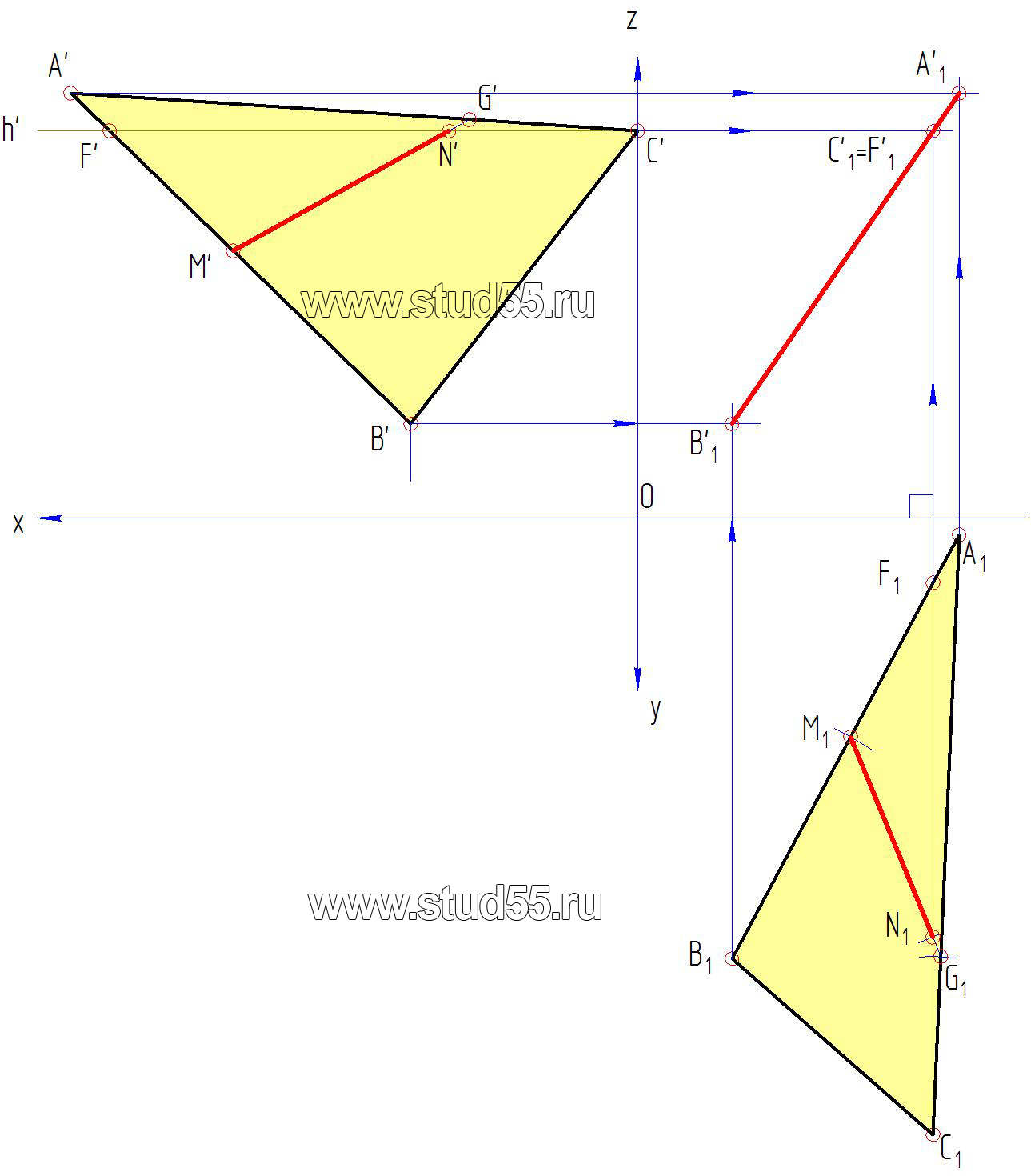
5. Методом плоскопараллельного перемещения определяем натуральную величину плоскости треугольника ABC, для чего:

а) в указанной плоскости через точку С(С) проводим фронталь C—F (С-F и C’-F’);

б) на свободном поле чертежа во горизонтальной проекции берем (отмечаем) произвольную точку С₁, считая, что это одна из вершин треугольника (конкретно вершина C). Из нее восстанавливаем перпендикуляр к фронтальной плоскости (через ось х);

Рис.1.5

в) плоскопараллельным перемещением переводим горизонтальную проекцию треугольника ABC, в новое положение A₁B₁C₁ таким образом, чтобы в фронтальной проекции он занял проецирующее положение (преобразовался в прямую линию). Для этого: на перпендикуляре от точки С₁, откладываем фронтальную проекцию горизонтали C₁—F₁ (длина l_CF) получаем точку F₁. Раствором циркуля из точки F₁ величиною F-A делаем дуговую засечку, а из точки C₁ — засечку величиной CA, тогда в пересечении дуговых линий получаем точку A₁ (вторая вершина треугольника);

— аналогично получаем точку B₁ (из точки C₁ делаем засечку величиной C—B (57мм), а из точки F₁ величиной F—B (90мм).Заметим, что при правильном решении три точки A₁ F’₁ и B’₁ должны лежать на одной прямой (сторона треугольника A₁—B₁)две другие стороны С₁—A₁ и C₁—B₁ получаются путем соединения их вершин;

г) из метода вращения следует, что при перемещении или вращении точки в какой-то плоскости проекций — на сопряженной плоскости проекция этой точки должна двигаться по прямой линии, в нашем конкретном случае по прямой параллельной оси х. Тогда проводим из точек A’B’C’ фронтальной проекции эти прямые (их называют плоскостями вращения точек), а из фронтальных проекций перемещенных точек A₁ В₁ C₁ восстановим перпендикуляры (линии связи) (рис.1.6).

Рис.1.6

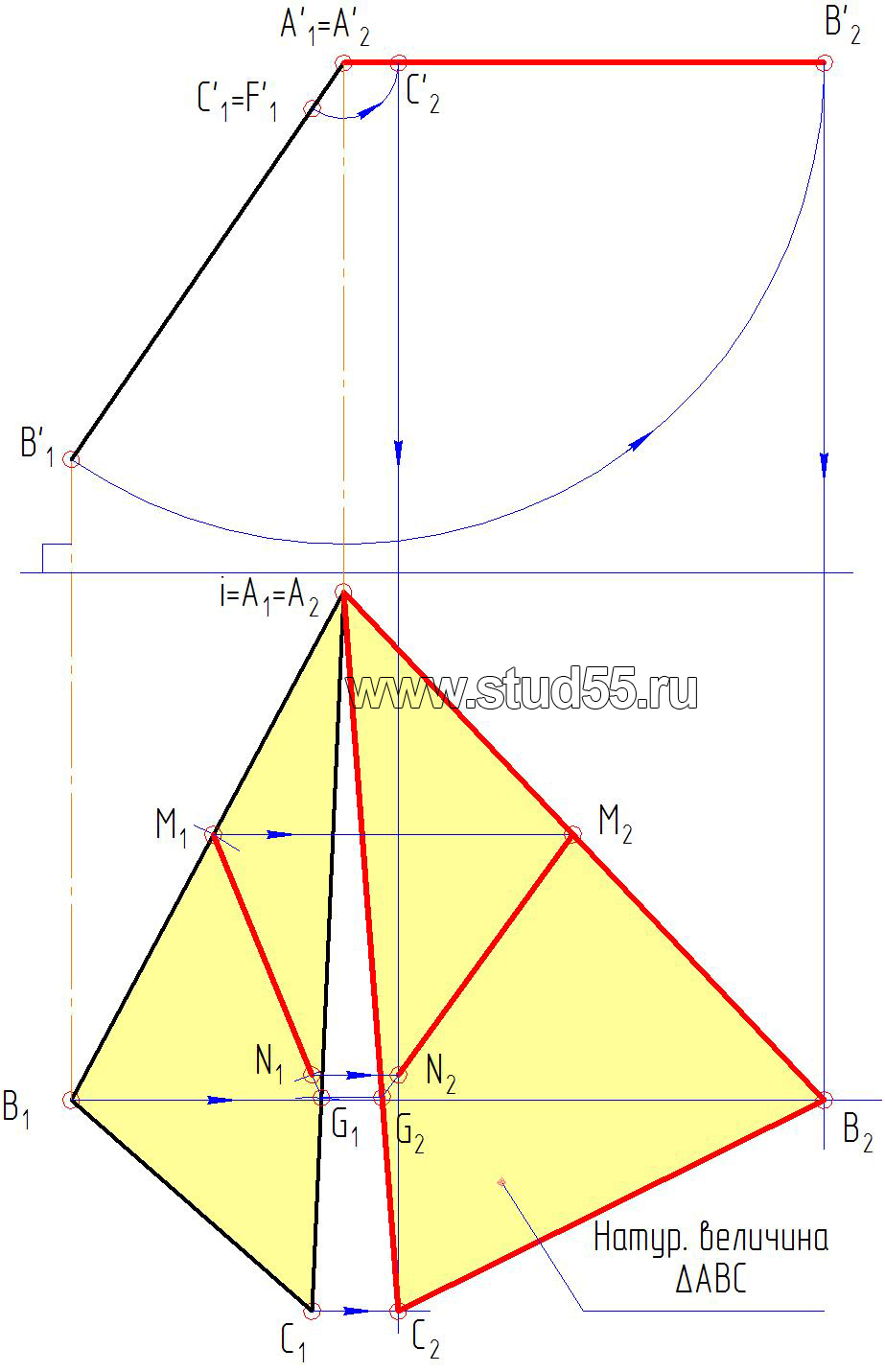
Пересечения указанных линий с соответствующими перпендикулярами дает новые положения фронтальной проекции треугольника ABC, конкретно A’₁В’₁C’₁ который должен стать проецирующим (прямой линией), поскольку горизонталь h₁ мы провели перпендикулярно фронтальной плоскости проекций (рис.1.6);

5) тогда для получения натуральной величины треугольника достаточно его фронтальную проекцию развернуть до параллельности с горизонтальной плоскостью. Разворот осуществляем с помощью циркуля через точку А’₁, считая ее как центр вращения, ставим треугольник A’₁В’₁C’₁ параллельно оси х, получаем A’₂В’₂C’₂. Как было сказано выше, при вращении точки, на сопряженной (теперь на горизонтальной) проекции они двигаются по прямым параллельным оси х. Опуская перпендикуляры (линии связи) из фронтальных проекций точек A’₂ В’₂ C’₂ пересечения их с соответствующими линиями находим горизонтальную проекцию треугольника ABC (A₂В₂C₂) в натуральную величину (рис.1.7).

Рис. 1.7

У меня есть все готовые решения задач с такими координатами, купить можно >>здесь

Цена 55 руб, чертежи по начертательной геометрии из книжки Фролова Вы легко можете скачать сразу после оплаты или я вышлю Вам на почту. Они находятся в ZIP архиве в различных форматах:
*.jpg – обычный цветной рисунок чертежа в масштабе 1 к 1 в хорошем разрешении 300 dpi;
*.cdw – формат программы Компас 12 и выше или версии LT;
*.dwg и .dxf — формат программы AUTOCAD, nanoCAD;

🎬 Видео

Сумма внутренних углов многоугольника. Выпуклые и невыпуклые многоугольники. 8 класс.Скачать

Определение истинной величины треугольника АВС. Метод плоско-параллельного перемещенияСкачать

Как доказать, что биссектрисы треугольника пересекаются в одной точке?Скачать

ПОСТРОИТЬ ПРАВИЛЬНЫЙ ПЯТИУГОЛЬНИК [construction a regular pentagon]Скачать