Пересечение плоскостей начертательная геометрия треугольники

Метки

Видео:Построение линии пересечения двух треугольников.Скачать

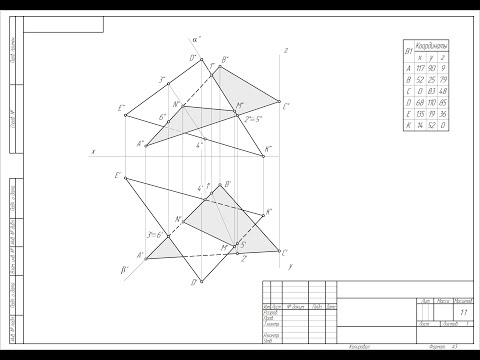
Линия пересечения плоскостей двух треугольников

Линия пересечения плоскостей двух треугольников начинают с построения точек по координатам. (на рисунке 1 представлены построенные плоскости)

1. Построение по координатам.

2. Выбираете какая из сторон плоскостей будет секущей . В данном случае возьмем Е₂D₂ ,принадлежащая плоскости Е₂D₂F₂, которая пересекает плоскость А₂В₂С₂ в точка 1₂ и 2₂.

Полученные точки, проецируют на стороны плоскости, которым они принадлежат, т.е С₁В₁ и А₁В₁.

Т.к. секущей является ЕD, то необходимо чтобы прямая 1₁2₁ пересекла секущую. В данном случае в точке К_{1.(Первая точка найдена)}

3. Одной точки мало будет. Повторим действия, описанные в пункте 2, но с отрезком E₂F₂.

E2F2 пересекает А₂В₂С₂ в точках 3₂ и 4₂. Проецируете на стороны А1С1 и А₁В₁.

Т.к. секущей является EF, то необходимо чтобы прямая 3₁4₁ пересекла секущую, но такого нет (не хватает немного отрезка). Для этого прямая 3₁4₁ продливается пока не пересечется с E₁F₁. Обозначаете точку (обозначил Н₁)._{(Но Н1 не является точкой пересечения, потому как на виде сверху принадлежит только одной плости)}

4. Соединяются точки К₁ и Н₁. Ближайшая точка, принадлежащая этой прямой и двум плоскостям, находится на стороне А₁В₁ плоскости А₁В₁С₁, обозначаем Р₁. _{(Вторая точка найдена)}

5. Найденные точки необходимо спроецировать на стороны плоскости, которым они принадлежат.

5. Обводите соответсвующими линиями контуры плоскостей, воспользовавшись методом конкурирующих точек.

Видео:Линия пересечения плоскостейСкачать

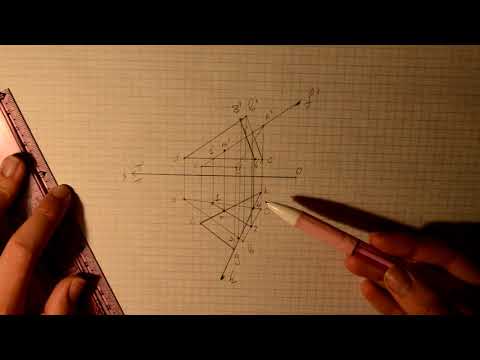
Построить линию пересечения треугольников ABC и EDK и показать видимость их в проекциях.
Определить натуральную величину треугольника ABC.

1. Строим проекции треугольника АВС.

2. Строим проекции треугольника EDK.

3. Находим точку пересечения стороны АС с треугольником EDK

4. Находим точку пересечения стороны А B с треугольником EDK и строим линию пересечения MN

5. С помощью конкурирующих точек 4 и 5 определяем видимость треугольников на фронтальной плоскости проекций.

6. С помощью конкурирующих точек 6 и 7 определяем видимость треугольников на горизонтальной плоскости проекций.

7. В треугольнике ABC проводим горизонталь CL и плоскопараллельным перемещением относительно горизонтальной плоскости проекций располагаем горизонталь перпендикулярно фронтальной плоскости проекций.

Строим фронтальную проекцию треугольника ABC . Треугольник должен проецироваться в прямую линию.

8. Определяем действительную величину треугольника ABC и строим на нем линию пересечения MN.

Видео:Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Построение линии пересечения плоскостей, заданных различными способами

Две плоскости пересекаются друг с другом по прямой линии. Чтобы её построить, необходимо определить две точки, принадлежащие одновременно каждой из заданных плоскостей. Рассмотрим, как это делается, на следующих примерах.

Найдем линию пересечения плоскостей общего положения α и β для случая, когда пл. α задана проекциями треугольника ABC, а пл. β – параллельными прямыми d и e. Решение этой задачи осуществляется путем построения точек L₁ и L₂, принадлежащих линии пересечения.

1. Вводим вспомогательную горизонтальную плоскость γ₁. Она пересекает α и β по прямым. Фронтальные проекции этих прямых, 1»C» и 2»3», совпадают с фронтальным следом пл. γ₁. Он обозначен на рисунке как f_0γ1 и расположен параллельно оси x.
2. Определяем горизонтальные проекции 1’C’ и 2’3′ по линиям связи.
3. Находим горизонтальную проекцию точки L₁ на пересечении прямых 1’C’ и 2’3′. Фронтальная проекция точки L₁ лежит на фронтальном следе плоскости γ.
4. Вводим вспомогательную горизонтальную плоскость γ₂. С помощью построений, аналогичных описанным в пунктах 1, 2, 3, находим проекции точки L₂.
5. Через L₁ и L₂ проводим искомую прямую l.

Стоит отметить, что в качестве пл. γ удобно использовать как плоскости уровня, так и проецирующие плоскости.

Видео:Построить линию пересечения треугольников ABC и DEF. Определить видимость. Вариант 2Скачать

Пересечение плоскостей, заданных следами

Найдем линию пересечения плоскостей α и β, заданных следами. Эта задача значительно проще предыдущей. Она не требует введения вспомогательных плоскостей. Их роль выполняют плоскости проекций П₁ и П₂.

1. Находим точку L’₁, расположенную на пересечении горизонтальных следов h_0α и h_0β. Точка L»₁ лежит на оси x. Её положение определяется при помощи линии связи, проведенной из L’₁.
2. Находим точку L»₂ на пересечении фронтальных следов пл. α и β. Точка L’₂ лежит на оси x. Её положение определяется по линии связи, проведенной из L»₂.
3. Проводим прямые l’ и l» через соответствующие проекции точек L₁ и L₂, как это показано на рисунке.

Таким образом, прямая l, проходящая через точки пересечения следов плоскостей, является искомой.

Видео:Нахождение пересечения двух треугольниковСкачать

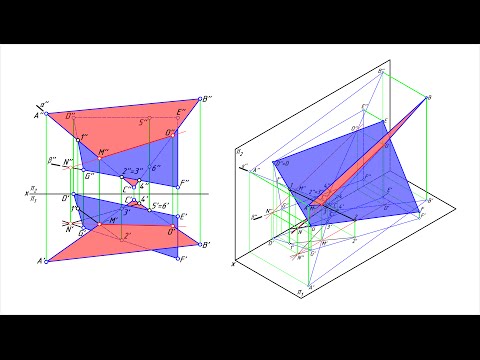
Пересечение плоскостей треугольников

Рассмотрим построение линии пересечения плоскостей, заданных треугольниками ABC и DEF, и определение их видимости методом конкурирующих точек.

1. Через прямую DE проводим фронтально-проецирующую плоскость σ: на чертеже обозначен ее след f_0σ. Плоскость σ пересекает треугольник ABC по прямой 35. Отметив точки 3»=A»B»∩f_0σ и 5»=A»С»∩f_0σ, определяем положение (∙)3′ и (∙)5′ по линиям связи на ΔA’B’C’.
2. Находим горизонтальную проекцию N’=D’E’∩3’5′ точки N пересечения прямых DE и 35, которые лежат во вспомогательной плоскости σ. Проекция N» расположена на фронтальном следе f_0σ на одной линии связи с N’.

Через прямую BC проводим фронтально-проецирующую плоскость τ: на чертеже обозначен ее след f_0τ. С помощью построений, аналогичных тем, что описаны в пунктах 1 и 2 алгоритма, находим проекции точки K.

Фронтально-конкурирующие точки 4 и 5, принадлежащие ΔDEF и ΔABC соответственно, находятся на одной фронтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π₂. Так как (∙)5′ находится ближе к наблюдателю, чем (∙)4′, то отсек ΔABC с принадлежащей ему (∙)5 является видимым в проекции на пл. π₂. С противоположной стороны от линии N»K» видимость треугольников меняется.

Горизонтально-конкурирующие точки 6 и 7, принадлежащие ΔABC и ΔDEF соответственно, находятся на одной горизонтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π₁. Так как (∙)6» находится выше, чем (∙)7», то отсек ΔABC с принадлежащей ему (∙)6 является видимым в проекции на пл. π₁. С противоположной стороны от линии N’K’ видимость треугольников меняется.

💥 Видео

Пересечение плоскостей (треугольника и четырёхугольника)Скачать

[Начертательная геометрия 1 курс] Пересечение двух плоскостей заданных треугольникамиСкачать

Взаимное пересечение двух плоскостейСкачать

Построение линии пересечения двух треугольников. Анимация.Скачать

Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

Построить линию пересечения треугольников ABC и DEF. Вариант 9Скачать

Начертательная геометрия 1 курс. Построить линию пересечения треугольников ABC и EDKСкачать

[Начертательная геометрия] Линия пересечения плоскостейСкачать

Построение линии пересечения двух плоскостейСкачать

Пересечение плоскостейСкачать

Нахождение точки пересечения прямой и треугольникаСкачать

Пересечение прямой линии с плоскостью Определение видимости прямойСкачать

Нахождение линии пересечения плоскостей путём приглашения плоскостей посредниковСкачать

Построить линию пересечения треугольника и параллелограмма.Скачать