Пересечение окружности с осью абсцисс (5 видео)

Пересечение окружности с осью абсцисс

Введем основные тригонометрические функции.

Пусть радиус-вектор $vec = bar$ точки $M$ образует угол $alpha$ с осью $Ox$ (рис.), причем $x$ и $y$ соответственно абсцисса и ордината конца $M$ вектора, $r$ — его модуль, а величина угла $alpha$ измеряется в градусах или в радианах.

1. Синусом угла $alpha$ (обозначение: $sin alpha$) называется отношение ординаты $y$ (см. рис.) к длине $r$ радиуса-вектора $bar $:

2. Косинусом угла $alpha$ (обозначение: $cos alpha$) называется отношение абсциссы $x$ к длине $r$ радиуса-вектора $bar $:

3. Тангенсом угла $alpha$ (обозначение: $tg alpha$) называется отношение синуса угла $alpha$ к косинусу этого угла:

4. Котангенсом угла $alpha$ (обозначение: $ctg alpha$) называется отношение косинуса угла $alpha$ к синусу этого угла:

5. Секансом угла $alpha$ (обозначение: $sec alpha$) называется величина, обратная $cos alpha$:

6. Косекансом угла $alpha$ (обозначение: $cosec alpha$) называется величина, обратная $sin alpha$:

Замечание 1. Тригонометрические функции (1) — (6) действительно являются функциями только угла $alpha$, т. е. не зависят от длины подвижного радиуса-вектора. Для того чтобы в этом убедиться, достаточно доказать, что если подвижный радиус-вектор $vec$ образует с осью абсцисс данный угол $alpha$, то отношения $frac$ и $frac$ не зависят от длины радиуса-вектора.

Замечание 2. Из определения $tg alpha$ и $ctg alpha$ следует, что

$tg alpha = frac$, (7)
$ctg alpha = frac$. (8)

Соотношения (7) и (8) можно было бы принять в качестве определений для $tg alpha$ и $ctg alpha$.

Замечание 3. Аналогично получаем

$sec alpha = frac$,(9)
$cosec alpha = frac$ (10).

Соотношения (9) и (10) можно было бы также принять в качестве определений для $sec alpha$ и $cosec alpha$.

Замечание 4. Во всех определениях (1) — (6) предполагаем, что соответствующие отношения существуют (имеют смысл). Например, $tg alpha$ имеет смысл, если $cos alpha neq 0, ctg alpha$ имеет смысл, если $sin alpha neq 0$, и т.д. Поскольку (замечание 1) тригонометрические функции (1) — (6) угла $alpha$ не зависят от длины подвижного радиуса-вектора, то в качестве радиуса-вектора можно брать вектор с длиной, равной единице $(| vec| = r = 1)$. Такой вектор называют единичным радиусом-вектором. В случае единичного радиуса-вектора формулы для основных тригонометрических функций запишутся так (рис.):

$begin sin alpha = y, cos alpha = x \ tg alpha = frac, ctg alpha = frac \ sec alpha = frac, cosec alpha = frac end$. (11)

Формулы для $tg alpha$ и $ctg alpha$ остались прежними (см. (7) и (8)), а формулы для остальных основных тригонометрических функций приняли более простой вид (см. (1), (2), (9) и (10)). Следовательно, синус и косинус угла а равны соответственно ординате и абсциссе конца подвижного единичного радиуса-вектора. Конец этого единичного радиуса-вектора при изменении угла а от $0^$ до $360^$ опишет окружность, называемую единичной окружностью (рис.). Для геометрического истолкования тангенса и котангенса вводят понятия оси тангенсов и оси котангенсов. Осью тангенсов называется перпендикуляр, восставленный в точке $A$ к неподвижному радиусу-вектору $bar$. Положительное и отрицательное направления на оси тангенсов выбирают так, чтобы они совпадали с соответствующими направлениями оси ординат (рис.). Рассмотрим угол $alpha = angle AOM$ и введем понятие соответствующей точки оси тангенсов.

а) Если точка $M$ единичной окружности лежит справа от оси ординат, то соответствующей ей точкой оси тангенсов назовем точку $M_$ (точку пересечения продолжения $MO$ с осью тангенсов, рис а.

б) Если точка $M$ единичной окружности лежит слева от оси ординат, то соответствующей ей точкой сси тангенсов назовем точку $M_$ (точку пересечения продолжения $MO$ с ссыо тангенсов, рис. б.

Заметим, что тангенс угла а численно равен ординате $y_$ (рис.) соответствующей точки сси тангенсов, т. е. всегда $tg alpha — y_$. Докажем это для углов первых двух четвертей:

1) $0^ leq alpha < 90^$ (рис. a), $tg alpha = frac<y_> = y_ geq 0$, где $y_$ — ордината точки $M_$.
2) $90^ < alpha leq 180^$ (рис. б). $tg alpha = frac<y_><x_> leq 0$, где $x_$ и $y_$ — абсцисса и ордината точки $M$. Из подобия прямоугольных треугольников $OMM_$ и $OM_A$ имеем

Следовательно, $tg alpha = frac<y_><x_> = y_ leq 0$.

Заметим еще следующее:
а) если точка $M$ лежит на оси ординат (например, $alpha = 270^$), то соответствующей ей точки сси тангенсов не существует, но при этом и $tg alpha$ также не существует;
б) в рассмотренных случаях 1)-2) мы брали угол $alpha$ в пределах от $0^$ до $360^$, но в наших рассуждениях ничего не изменится, если мы будем предполагать угол $alpha$ любым.

Осью котангенсов называется перпендикуляр, восставленный в точке В (конец радиуса-вектора $bar $, образующего с осью $Ox$ угол, равный $90^$) к оси ординат. Положительное и отрицательное направления на оси котангенсов выбирают так, чтобы они совпадали с соответствующими направлениями оси абсцисс (рис.). Введем понятие соответствующей точки оси котангенсов.

а) Если точка $M$ единичной окружности лежит над осью абсцисс, то соответствующей ей точкой оси котангенсов назовем точку $M_$ (точку пересечения продолжения $OM$ с осью котангенсов, рис. а).

б) Если точка $M$ единичной окружности лежит под осью абсцисс, то соответствующей ей точкой сси котангенсов назовем точку (точку пересечения продолжения $MO$ с осью котангенсов, рис. б).

Аналогично предыдущему можно получить, что котангенс угла $alpha$ равен абсциссе $x_$ соответствующей точки оси котангенсов, т. е. $ctg alpha = x_$. Если точка $M$ лежит на оси абсцисс (например, $alpha — 180^$), то соответствующей ей точки оси котангенсов не существует, но при этом и $ctg alpha$ также не существует.

Содержание

Пересечение с осями онлайн
Другие полезные разделы:
Оставить свой комментарий:
Прямоугольная система координат. Ось абсцисс и ординат
Прямоугольная декартова система координат
Координаты точки в декартовой системе координат
📺 Видео

Видео:Алгоритмы. Пересечение окружностейСкачать

Пересечение с осями онлайн

Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha, предназначен для решения задачи нахождения точек пересечения графика функции с осями координат.

Найти точки пересечения функции с осями координат:

При проведении исследования функции, возникает задача нахождения точек пересечения этой функции с осями координат. Рассмотрим на конкретном примере алгоритм решения такой задачи. Для простоты будем работать с функцией одной переменной:

График данной функции представлен на рисунке:

Как следует из рисунка, наша функция пересекает ось в двух точках, а ось — в одной.

Сначала найдём точки пересечения функции с осью . Сразу отметим, что в этих точках координата . Поэтому для их поиска, нам нужно решить уравнение:

Таким образом, мы нашли две точки пересечения нашей функции с осью абсцисс: и . Стоит отметить, что задача поиска пересечений функции с осью эквивалентна задаче нахождения нулей функции.

Теперь найдём точку пересечения с осью ординат. В этой точке координата . Поэтому для их поиска, просто подставляем значение в нашу функцию:

Таким образом, мы нашли точку пересечения нашей функции с осью ординат .

Видео:Теорема о числе точек пересечения двух окружностейСкачать

Другие полезные разделы:

Видео:Система координат · Ось абсцисс и ось ординат · Координатная плоскость Урок Математики для 6 классаСкачать

Оставить свой комментарий:

Мы в социальных сетях:
Группа ВКонтакте | Бот в Телеграмме

Видео:Координатная плоскость | Ось абсцисс | Ось ординат | МегаШкола | Математика 6 классСкачать

Прямоугольная система координат. Ось абсцисс и ординат

О чем эта статья:

Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Прямоугольная декартова система координат

Французский математик Рене Декарт предложил вместо геометрических построений использовать математические расчеты. Так появился метод координат, о котором мы сейчас расскажем.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты школы тоже можно записать числами — они помогут понять, где именно находится наша школа. С точками на плоскости та же история.

Координатой можно назвать номер столика в кафе, широту и долготу на географической карте, положение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем какой-то объект набором букв, чисел или других символов, тем самым мы задаем его координаты.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

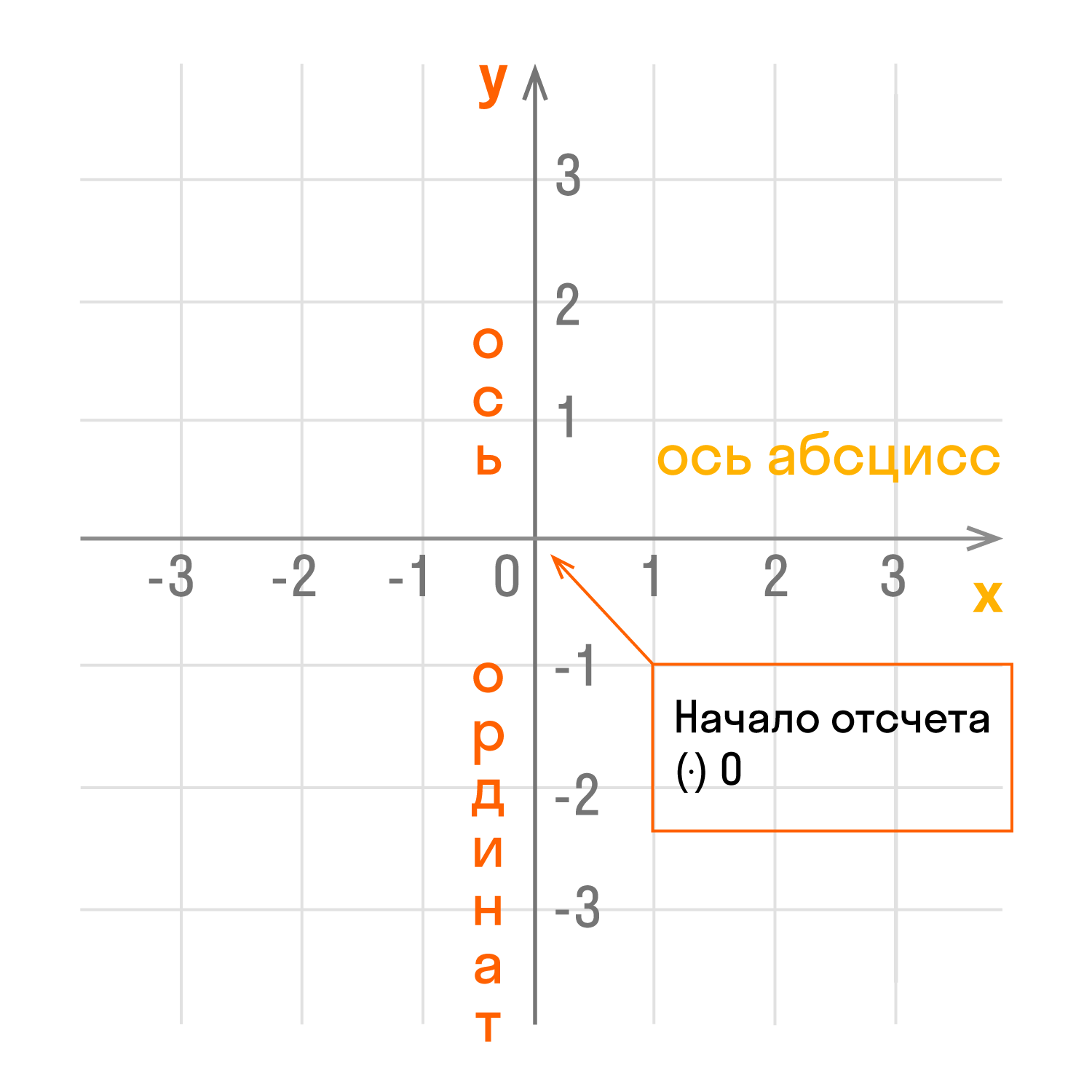
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

Координатные оси — это прямые, образующие систему координат.
Ось абсцисс Ox — горизонтальная ось.
Ось ординат Oy — вертикальная ось.
Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.

Единичные отрезки располагаются справа и слева от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy располагаются слева или справа, на оси Ox — внизу под ней. Чаще всего единичные отрезки двух осей соответствуют друг другу, но бывают задачи, где они не равны.

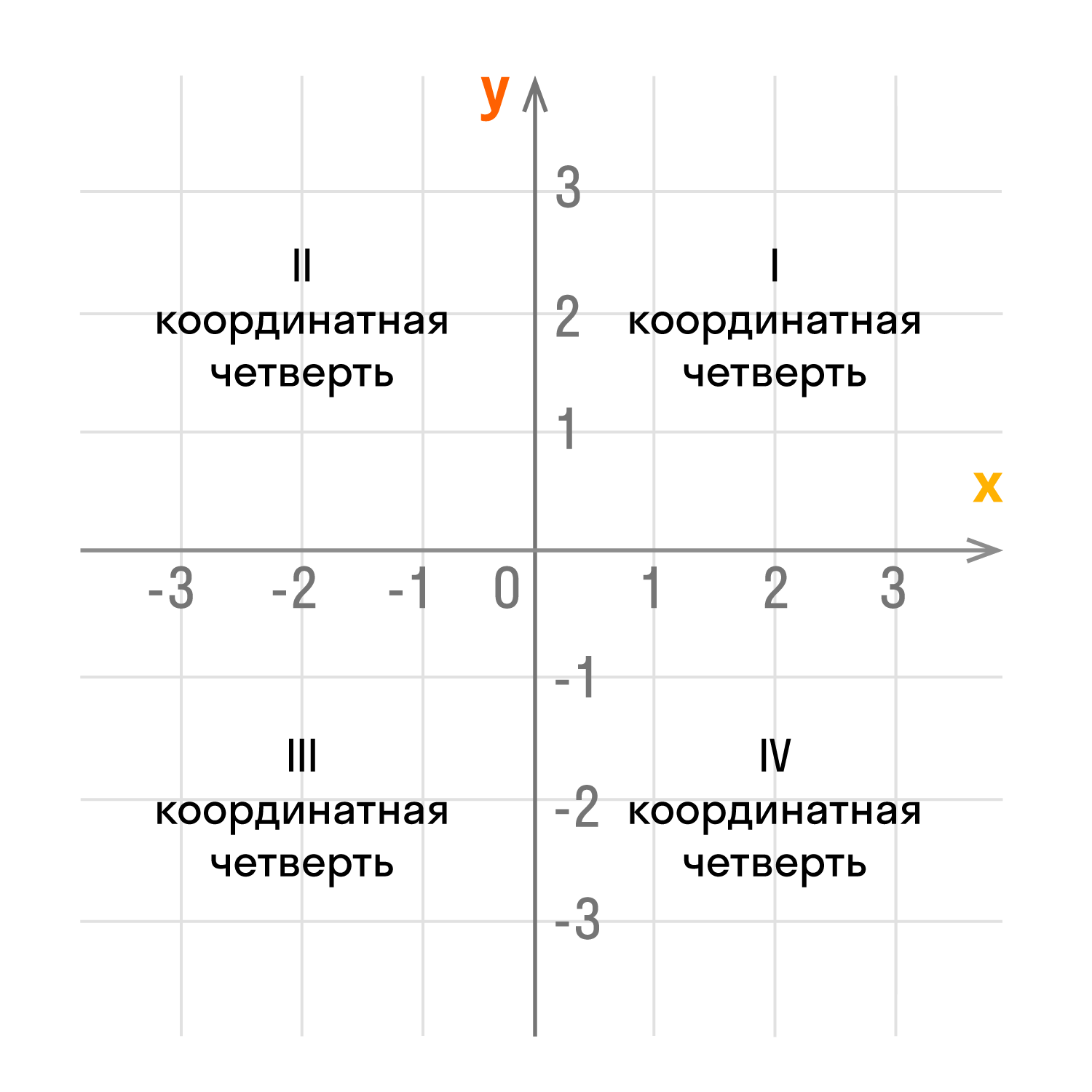
Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

верхний правый угол — первая четверть I;
верхний левый угол — вторая четверть II;
нижний левый угол — третья четверть III;
нижний правый угол — четвертая четверть IV;

Чтобы узнать координаты точки в прямоугольной системе координат, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты записывают в скобках, первая по оси Ох, вторая по оси Оу.

Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
Если обе координаты отрицательны, то число находится в третьей четверти.
Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Координаты точки в декартовой системе координат

Для начала отложим точку М на координатной оси Ох. Любое действительное число x_M равно единственной точке М, которая располагается на данной прямой. При этом начало отсчета координатных прямых всегда ноль.

Каждая точка М, которая расположена на Ох, равна действительному числу x_M. Этим действительным числом и является ноль, если точка М расположена в начале координат, то есть на пересечении Оx и Оу. Если точка удалена в положительном направлении, то число длины отрезка положительно и наоборот.

Число x_M — это координата точки М на заданной координатной прямой.

Пусть точка будет проекцией точки M_x на Ох, а M_y на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, после чего получим соответственные точки пересечения M_x и M_y.Тогда у точки M_x на оси Оx есть соответствующее число x_M, а M_y на Оу — y_M. Как это выглядит на координатных осях:

Каждой точке М на заданной плоскости в прямоугольной декартовой системе координат соответствует пара чисел (x_M, y_M), которые называются ее координатами. Абсцисса М — это x_M, ордината М — это y_M.

Обратное утверждение тоже верно: каждая пара (x_M, y_M) имеет соответствующую точку на плоскости.