Перечислите все элементы треугольника

Треугольник – это геометрическая фигура, состоящая из трех точек, попарно соединенных между собой отрезками. Точки называются вершинами треугольника, отрезки – сторонами треугольника. Треугольник имеет три вершины и три стороны. Стороны треугольника обозначаются часто малыми буквами, которые соответствуют заглавным буквам, обозначающим противоположные вершины.

Внутренние углы треугольника – это углы, образованные его сторонами. Угол А – это угол, образованный сторонами АВ и АС.

Виды треугольников по углам:

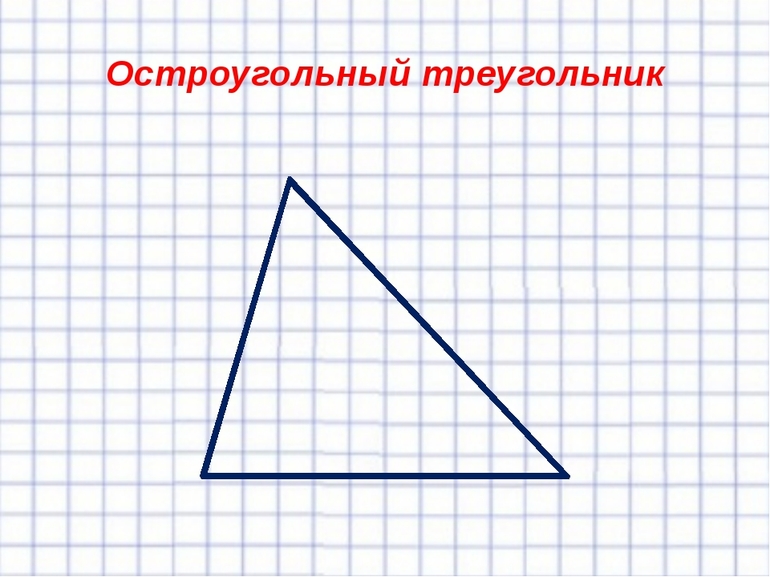
1. Остроугольный треугольник – это треугольник, все углы которого острые (то есть градусная мера каждого угла меньше 90º).
2. Прямоугольный треугольник – это треугольник, у которого один угол прямой (то есть имеет градусную меру 90º).
3. Тупоугольный треугольник – это треугольник, у которого один угол тупой (то есть имеет градусную меру больше 90º).

Виды треугольников по сторонам:

1. Равносторонний треугольник (или правильный треугольник) – это треугольник, у которого все три стороны равны.
2. Равнобедренный треугольник – это треугольник, у которого две стороны равны.
3. Разносторонний треугольник – треугольник, все стороны которого имеют разную длину.

Элементы треугольника

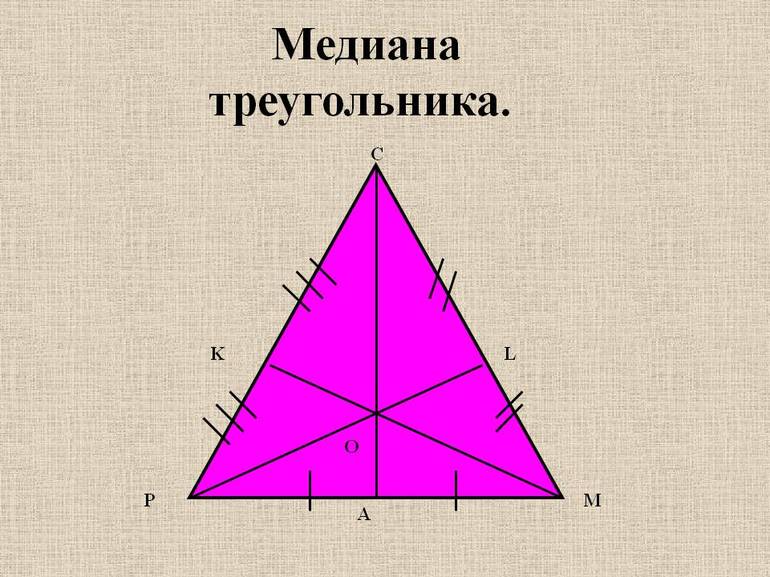
Медиана – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Любой треугольник имеет три медианы, которые пересекаются в одной точке. Эта точка пересечения называется центроидом или центром тяжести треугольника. Центроид делит каждую медиану в отношении 1:2, считая от основания медианы.

Биссектриса – это отрезок, делящий угол треугольника на две равные части. Любой треугольник имеет три биссектрисы, которые пересекаются в одной точке.

Высота – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону. Любой треугольник имеет три высоты, которые пересекаются в одной точке, называемой ортоцентром треугольника.

Средняя линия треугольника – это отрезок, соединяющий середины двух его сторон.

Средняя линия треугольника, соединяющая середины двух его сторон, параллельна третьей стороне и равна ее половине: (MN=frac12AC; MNparallel AC) .

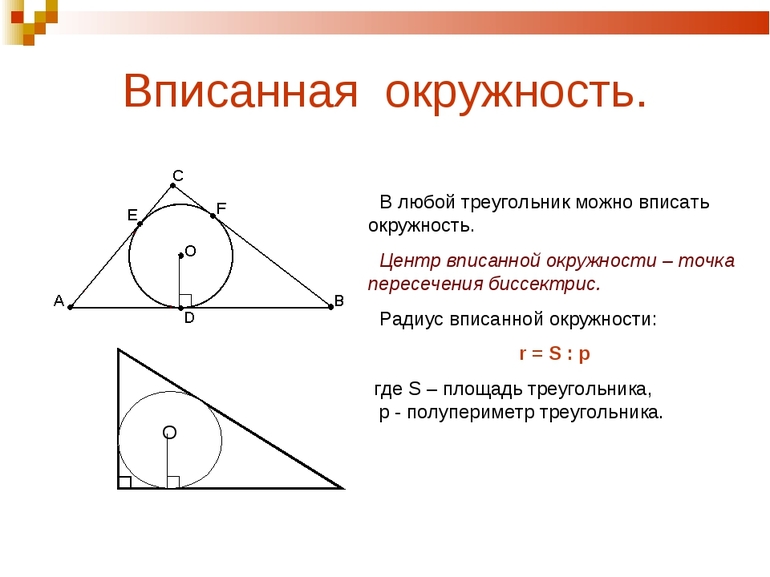
Серединный перпендикуляр к отрезку – прямая, перпендикулярная к этому отрезку и проходящая через его середину. Три срединных перпендикуляра треугольника пересекаются в одной точке, являющейся центром описанного круга.

Основные свойства треугольников

1. Против большей стороны лежит больший угол, и наоборот.
2. Против равных сторон лежат равные углы, и наоборот. В частности, все углы в равностороннем треугольнике равны.
3. Сумма углов треугольника равна 180º. Из двух последних свойств следует, что каждый угол в равностороннем треугольнике равен 60º.
4. Продолжая одну из сторон треугольника, получаем внешний угол. Внешний угол треугольника равен сумме внутренних углов, не смежных с ним.
5. Любая сторона треугольника меньше суммы двух других сторон и больше их разности (a b – c; b a – c; c a – b).

Один из внешних углов треугольника равен 65 (^circ) . Углы, не смежные с данным внешним углом, относятся как 6:7. Найдите наибольший из них.

Внутренние углы треугольника относятся как 3:7:8. Найдите отношение внешних углов треугольника.

Чему равна градусная мера одного из углов прямоугольного треугольника?

Если в треугольнике один угол больше суммы двух других углов, то он

Если в треугольнике один внешний угол острый, то этот треугольник

Периметр равнобедренного треугольника равен 11 см, а основание равно 3 см. Найдите боковую сторону треугольника.

Видео:Треугольник и его элементыСкачать

Элементы треугольника — формулы вычисления основных параметров

Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Общие сведения

Произвольное множество точек называют геометрической фигурой. На плоскости они соединены замкнутыми линиями, образующими контур тела. В трёхмерном пространстве многоугольник, состоящий из трёх отрезков, не принадлежащих одной прямой, носит имя треугольник. Его линии называют сторонами или боковыми гранями, а место их пересечения — вершинами.

Треугольник — замкнутое геометрическое тело, состоящее из трёх сторон и такого же количества углов. Боковые грани принято обозначать маленькими латинскими буквами. Углы на рисунке показывают маленькой дугой, а в записи — символом ∠ с указанием соответствующей вершины. Точки же пересечения линий подписывают большими буквами.

Например, если имеется треугольник ABC, у него есть углы A, B, C и стороны a, b, c. Боковые грани могут обозначать и как отрезки, тогда в их имени учитываются ограничивающие точки. Например, AB, BC, CA. Строгого требования в виде обозначений нет, но существуют негласные правила, которых всё же рекомендуется придерживаться.

Хотя определение треугольника и его элементов одинаковое, выделяют 3 класса фигур:

• остроугольный — любой из углов тела не превышает 90 градусов;
• тупоугольный — форма одного из разворотов тупоугольная;
• прямоугольный — размер одного из трёх углов составляет 90 градусов.

Кроме этого, многоугольник классифицируют по числу равных сторон. Разносторонним он считается в том случае, если все они разной длины, равнобедренным — треугольник, имеющий 2 равные стороны, а равносторонним — у которого все стороны равны. Последний в литературе может ещё называться правильным.

На основании классификационных групп треугольники можно сравнивать между собой. Они считаются подобными, если 2 угла одного соответственно равны двум углам другого, или когда 2 стороны одного пропорциональны двум сторонам другого, а углы, заключённые между этими сторонами, равны. Эти правила называют признаками подобия. Они особенно популярны среди физиков. Их часто используют при вычислении элементов прямоугольников, квадратов, трапеций.

Видео:Треугольники. 7 класс.Скачать

Элементы треугольника

Кроме сторон и вершин, фигура имеет различные точки и линии, называемые замечательными. Такое имя они получили из-за своих свойств. Но перед тем как их перечислить, нелишним будет привести основные величины, характеризующие фигуру, способы их нахождения и теоремы.

Периметр многоугольника можно определить, сложив все стороны: P = a + b + c. Площадь треугольника находится как половина произведения двух граней, умноженных на синус угла между ними: S = (a * b * sinC) / 2. Сумма углов равна 180 градусов, при этом напротив равных сторон лежат одинаковые углы.

К замечательным линиям относят:

1. Медиану — линию, проходящую через вершину к середине противолежащей стороны. Всего в треугольнике можно провести 3 таких отрезка. Точка их пересечения является центром массы. Если считать от вершины, в ней она делится в отношении 2 к 1. Каждая медиана разделяет фигуру на 2 объекта с одинаковой площадью.
2. Биссектрису — отрезок, построенный к стороне из угла и делящий его на 2 равные части. Она делит грань на 2 замкнутые линии, пропорциональные прилежащим сторонам. Точка, в которой пересекаются биссектрисы, является началом диаметра вписанной в треугольник окружности.
3. Высоту — перпендикуляр, опущенный из угла на противоположную сторону. Все они пересекаются в одной точке.
4. Срединную линию — проходит всегда параллельно одной из граней и соединяет середины двух оставшихся сторон. 3 таких линии разделят многоугольник на 4 равных треугольника.

При измерениях используют и «особенные» точки фигуры. Если в треугольник вписать окружность, её центр совпадёт с местом скрещивания перпендикуляров. А если поместить в круг, середина будет совпадать с пересечением биссектрис. Для других замечательных линий точки их соприкосновения также имеют свои названия: ортоцентр (высот) и центроид (медиан). Первая может принадлежать как внутренней площади фигуры, так и внешней (тупоугольный треугольник).

В равнобедренном треугольнике медиана, высота и биссектриса совпадают. При этом их центр является серединой как вписанной окружности, так и описанного круга. А угол, из которого построен один из таких отрезков, будет разделён на 2 одинаковых разворота равных 30 градусам.

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Основные формулы

Найти любой элемент треугольника можно по специальным формулам. Чаще всего приходится искать стороны фигуры. Зная их, можно найти практически любые параметры, просто подставив в выражения значения размеров граней.

Найти длину отрезка, формирующего контур фигуры, можно, зная длины двух сторон и угла или значения двух углов и одной стороны. Для первого случая формула имеет вид a = b * sin (a) / sin (b) = b * sin (a) / sin (a + c), а второго: a = √(b 2 + c 2 — 2bc * cos (a)). Если имеется тупой угол, косинус будет отрицательный. Это необходимо учитывать при расчётах.

Это общие формулы, подходящие для любого типа треугольника. Но в то же время для прямоугольного существует своё правило, связывающее все 3 грани в одну формулу: c = √(b 2 + a 2 ). Называется оно теоремой Пифагора. В равнобедренном вычислить сторону можно, зная любую другую и угол. Для основания используют равенство b = 2a * cos (a), а для равных граней: a = b / 2 * cos (a).

Из множества других существующих формул для определения различных элементов фигуры, можно указать на те, что чаще всего используются при решении примеров:

1. Высота: h = (2 / a) * √(p * (p — a) * (p — b) * (p — c)) или h = b * sin© = c * sin (b). Отрезок можно найти, зная площадь и сторону h = 2 * S / a или радиус описанной окружности: h = (b * c) / 2 * R.
2. Биссектриса: L = √(a * b * (a + b + c) * (a + b — c)) / (a + b). Формулу можно упростить, используя периметр: L = 2 * √ (a * b * P) * (P — c)) / (a + b), где P = p /2 (полупериметр).
3. Медиана: М = √(2 * a 2 + 2b 2 — c 2 ) / 2. Линию можно определить, зная только 2 стороны и лежащий между ними угол: М = √(a 2 + b 2 — 2 * a * b * cos (с)) / 2. В прямоугольном треугольнике она равняется радиусу описанного круга или половине гипотенузы: М = R = c / 2.

Существуют и упрощённые выражения. Формула Герона позволяет высчитать площадь, используя полупериметр и длины сторон: S = √(P * (P — a) * (P — b) * (P — c)). Также величину можно определить, зная высоту и длину основания: S = (a * H) / 2.

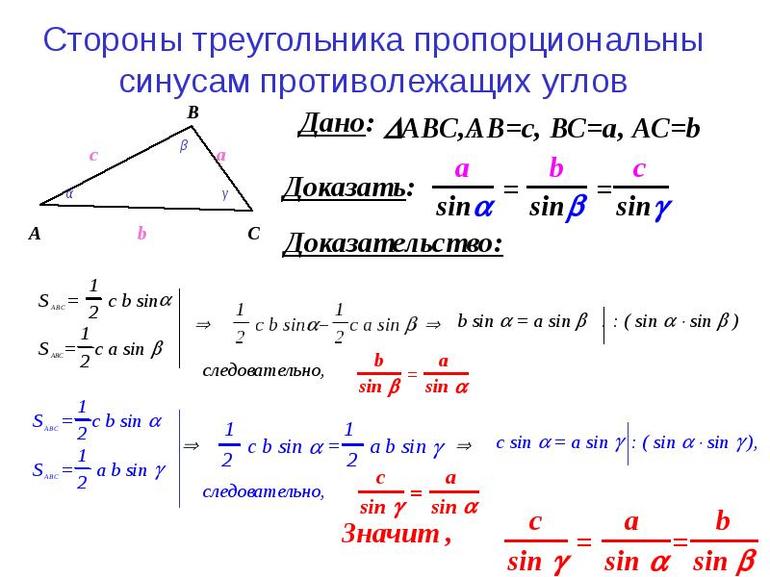
Для нахождения элементов треугольника в 7 классе ученикам дают ещё 2 фундаментальные теоремы: косинусов и синусов. Первая сообщает, что квадрат грани фигуры равен удвоенному произведению двух сторон и косинуса угла между ними, вычтенному из сумы квадратов: a 2 = b 2 + c 2 — 2 * b * c * cos (a). Согласно же второй, стороны пропорциональны синусам противолежащих углов: a / sin (a) = b / sin (b) = c / sin©.

Видео:9 класс, 15 урок, Решение треугольниковСкачать

Решение примеров

Формул для вычисления элементов треугольников можно насчитать несколько десятков. Запомнить их довольно сложно, поэтому нужно выучить основные определения и выражения, а сделать это лучше всего, решая практические примеры. Вот некоторые из них:

1. В треугольнике проведено 2 высоты. Одна равняется 63 см, а другая 56 см. Найти истинный отрезок, если основание AC = 84 см, а размер медианы BK совпадает с длиной стороны BC. Так как точка K делит отрезок AC пополам, AK = KC = AC / 2 = 84 /2 = 42 см. В треугольнике BKC 2 стороны равны друг другу, согласно условию, значит, он равнобедренный. Следовательно, высота является одновременно и медианой. KH = HC = MC /2 = 42 / 2 = 21 см. Искомый отрезок будет равен: h = AK + KC = 42 + 21 = 63 см. Следовательно, правильный первый вариант.
2. Пусть дан треугольник ABC. Найти возможный отрезок BN, на который биссектриса поделит сторону BC, если AB = 6 см, BC = 7 см, AC = 8 см. Для решения понадобится вспомнить свойство биссектрисы. Из него следует, что BN / NC = AB / AC = 6 / 8. Если искомый отрезок принять за икс, будет верным равенство KC = 7 — x. Значит: x / (7 — x) = 6 / 8. Отсюда можно выразить неизвестное: x = 42 / 14 = 3 см. Теперь останется подставить найденное число и найти искомое значение: KC = 7 — 3 = 4 см.
3. Завод начал выпускать новую серию объёмных фигур. Определить, какой тип многоугольника лежит в их основании, если её стороны равны 3, 2 и √3. Чтобы найти ответ, нужно проанализировать исходные данные. Так как сумма двух меньших сторон больше третей боковой грани, в основании лежит треугольник. 3 в квадрате не равно 2 2 + (√3) 2 . Следовательно, геометрическое тело непрямоугольное. По теореме косинусов можно записать: a 2 = b 2 + c 2 — 2 * b * c * cos (a). Исходя из того, что cos (a) = -1/ √ 3, то есть он отрицательный, можно утверждать, что разворот угла тупой. Значит, треугольник у основания тупоугольный.

Проверить правильность вычислений можно, воспользовавшись онлайн-калькуляторами. Это сервисы, предоставляющие услуги по расчёту различных математических величин. Воспользоваться ими сможет любой, даже тот, кто не знает ни одной формулы и теоремы. Всё, что требуется от пользователя — правильно ввести исходные данные в специальную форму и нажать кнопку «Рассчитать». Через несколько секунд ответ, а в некоторых случаях и решение, появится на экране.

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Что такое элементы треугольника?

Что такое элементы треугольника? — Наука

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Содержание:

В элементы треугольника они делятся на первичные и вторичные. Они составляют его компоненты и как таковые определяют. Треугольник — это трехсторонний многоугольник, сумма углов которого равна 180 градусам.

Первичные элементы соответствуют вершинам, сторонам и углам, они могут быть внутренними или внешними.

Второстепенные относятся к высоте, ортоцентру, биссектрисе, центру, биссектрисе, центру описанной окружности и медиане. Обычно в тригонометрии время уделяется только изучению основных элементов и дополнительно к высоте.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Основные элементы треугольника

Когда дело доходит до изучения геометрических фигур, треугольники играют ключевую роль, поскольку они считаются простейшими существующими многоугольниками, поскольку у них всего 3 стороны. Любой многоугольник с 4 или более сторонами можно разделить на конечное число треугольников.

Видео:Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать

Вершины

Они являются исходными точками треугольника. Визуально вершину можно определить как место, где рождаются линии многоугольника и которые определяют его границы.

Их легко узнать, так как они определяют общий размер фигуры. Обычно их обозначают заглавными буквами A, B и C.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Стороны

Это каждая из линий, составляющих треугольник. Одна сторона — это пространство между двумя вершинами, обозначенными прямой линией.

Обычно они обозначаются буквами вершин на концах, например сторона AB, или строчными буквами a, b и c, расположив их на противоположной стороне вершин A, B и C.

Сумма длин сторон треугольника называется периметром.

Видео:ВСЕ ВИДЫ ТРЕУГОЛЬНИКОВ😉 #егэ #огэ #математика #профильныйегэ #shorts #геометрия #образованиеСкачать

Углы

Это степень разделения двух сторон, начинающихся от одной и той же вершины (внутренний угол), измеряется в градусах.

Сумма всех углов в треугольнике всегда 180 градусов. Также можно измерить внешний угол, в этом случае необходимо удлинить одну из сторон.

Углы обозначаются греческими буквами, такими как альфа (α), бета (β) или гамма (γ).

Видео:Признаки равенства треугольников. 7 класс.Скачать

Высота

Это мера перпендикулярной линии (которая образует угол в 90 градусов), которая проходит от одной вершины к противоположной стороне.

Оно обозначается строчной буквой h. Треугольник может иметь 3 разных высоты в зависимости от измеряемой вершины.

Видео:Формулы равностороннего треугольника #shortsСкачать

Ортоцентр

При нанесении трех высот треугольника точка, в которой соприкасаются три линии, является ортоцентром. Обычно обозначается буквой H.

Видео:7 класс. Треугольник: основные элементы, главные отрезкиСкачать

Биссектриса

Это линия, идущая от одной вершины к центру противоположной стороны треугольника, поэтому она «делит» угол пополам. В зависимости от типа треугольника высота и биссектриса могут быть одинаковыми.

Видео:7 класс, 15 урок, Первый признак равенства треугольниковСкачать

Incenter

Это точка, где встречаются 3 биссектрисы.

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Медиатр

Также известная как симметричная линия, это линия, перпендикулярная одной стороне треугольника, проходящая через его середину.

Видео:2 Элементы треугольникаСкачать

Окружной центр

Это общая точка пересечения трех медиатрис. Если нарисовать круг, который касается трех вершин треугольника, центр описанной окружности будет центром круга.

Видео:1.3. Треугольники и их элементы. Высоты.Скачать

Медиана

Это линия, соединяющая середины двух сторон.

Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Ссылки

1. Что такое вершина в геометрии (н.ф.). Получено 30 ноября 2017 г. из Study.
2. Элементы треугольника (н.д.). Получено 30 ноября 2017 г. из CEIBAL.
3. Элементы треугольника (н.ф.). Получено 30 ноября 2017 г. из Интернет-профессора.
4. Вторичные элементы треугольника (н.ф.). Получено 30 ноября 2017 г. из Узингго.
5. Каролина Педроза (s.f.). Элементы треугольника. Получено 30 ноября 2017 г. с сайта Modern Mathematics.

Экономические явления: понятие, характеристика и примеры

🎬 Видео

Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать