Паркет из треугольников и шестиугольников (8 видео)

Паркет из треугольников и шестиугольников

И.М. СМИРНОВА, В.А. СМИРНОВ

Паркеты с древних времен привлекали к себе внимание людей. Ими мостили дороги, украшали полы в помещениях, стены домов, использовали в декоративно-прикладном искусстве. Знаменитый голландский художник Мариус Эшер (1898-1972) посвятил паркетам несколько своих картин. Среди них: «Всадники» (рис. 1), «Ящерицы» (рис. 2), «Летящие птицы» (рис. 3).

Проявление свойств паркетов сказывается на свойствах различных природных минералов и кристаллов. В то же время паркеты являются объектом исследования математиков. Глубокие результаты здесь получены отечественными учеными, академиками: А.Д. Александровым, Б.Н. Делоне, Е.С. Федоровым и др.

Здесь мы рассмотрим паркеты на евклидовой плоскости, на плоскости Лобачевского, на сфере и в пространстве.

1. Паркеты на плоскости

Паркетом на плоскости называется такое заполнение плоскости многоугольниками, при котором любые два многоугольника либо имеют общую сторону, либо имеют общую вершину, либо не имеют общих точек.

Паркет называется правильным, если он состоит из равных правильных многоугольников.

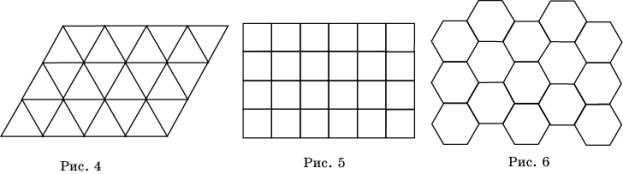
Примеры правильных паркетов дают заполнения плоскости:

а) правильными треугольниками (рис. 4);

б) квадратами (рис. 5);

в) правильными шестиугольниками (рис. 6).

Докажем, что другими равными правильными многоугольниками заполнить плоскость нельзя. Действительно, углы правильного n -угольника равны . Заполним таблицу, состоящую из углов правильных n -угольников.

108

120

128 4 /₇

135

140

144

147 3 /₁₁

150

Если в одной вершине паркета сходится m правильных n — угольников, то должно выполняться равенство откуда

Возможными допустимыми значениями n являются 3, 4 и 6. При остальных значениях n число m оказывается дробным. В частности, нельзя заполнить плоскость правильными пятиугольниками.

Можно подумать, что наличие только трех видов правильных паркетов обусловлено исключительно значениями углов правильных многоугольников, и если отказаться от требования правильности многоугольников, то число паркетов увеличится.

На самом деле, это не так. Даже, если отказаться от выпуклости многоугольников, или допускать в качестве сторон многоугольников кривые линии, т.е. рассматривать криволинейные многоугольники, то при некоторых естественных ограничениях на размеры многоугольников (о которых речь пойдет ниже) имеется только три вида таких паркетов:

1) из треугольников, в каждой вершине которого сходится шесть сторон;

2) из четырехугольников, в каждой вершине которого сходится четыре стороны;

3) из шестиугольников, в каждой вершине которого сходится три стороны.

Мы не будем доказывать это утверждение в общем виде, а рассмотрим несколько примеров, показывающих причину его справедливости.

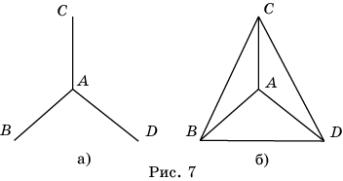
Например, выясним, можно ли составить паркет из треугольников, в каждой вершине которого сходится три стороны.

Пусть в вершине A сходится три стороны AB , AC и AD (рис. 7, а). Так как паркет состоит из треугольников, то вершины B , C и D попарно должны соединяться линиями (рис. 7, б). Но в этом случае в вершинах B , C и D будет сходиться по три стороны и ни одной стороны нельзя будет добавить для продолжения паркета. Таким образом, фигуру на рисунке 7, б нельзя достроить до паркета на всей плоскости, т.е. искомого паркета не существует.

Самостоятельно покажите, что не существует паркета из треугольников, в каждой вершине которого сходится: а) четыре стороны; б) пять сторон.

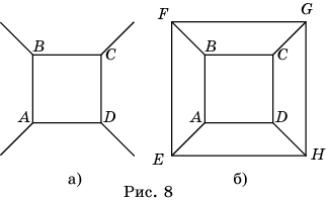
Покажем, что не существует паркета, состоящего из четырехугольников, в каждой вершине которого сходится три стороны.

Рассмотрим четырехугольник ABCD (рис. 8, а). Из каждой его вершины должно выходить дополнительно по одной стороне AE , BF , CG , DH . Так как паркет состоит из четырехугольников, то концы этих сторон E , F , G , H должны попарно соединяться линиями (рис. 8, б). Но в этом случае в вершинах E , F , G и H будет сходиться по три стороны и ни одной стороны нельзя будет добавить для продолжения паркета. Таким образом, фигуру на рисунке 8, б нельзя достроить до паркета на всей плоскости, т.е. искомого паркета не существует.

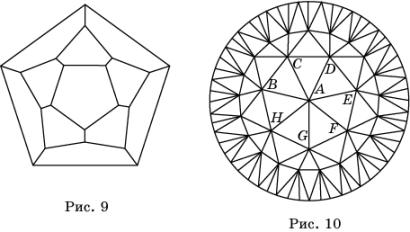
Используя рисунок 9, самостоятельно покажите, что не существует паркета из пятиугольников, в каждой вершине которого сходится три стороны.

Выясним, существует ли паркет из треугольников, в каждой вершине которого сходится семь сторон.

Попробуем построить такой паркет. Начнем с вершины A , в которой сходится семь сторон. Расположим их концы B , C , D , E , F , G , H на окружности и соединим их хордами (рис. 10). В результате получим семь треугольников с общей вершиной A . Из вершин этих треугольников, отличных от A , должно дополнительно выходить по четыре стороны. Расположим концы этих сторон на окружности и соединим их хордами. В результате получим еще 28 треугольников. Этот процесс можно продолжать. Однако при этом придется или уменьшать стороны треугольников, являющиеся хордами окружностей, или увеличивать стороны треугольников, соединяющие вершины на соседних окружностях. Если же мы ограничим стороны треугольников снизу некоторым числом >0 и сверху некоторым числом >0, то, начиная с некоторого шага, построение паркета будет невозможным.

Оказывается, что не только это, но и никакое другое построение паркета из треугольников, в каждой вершине которого сходится семь сторон с указанными ограничениями, невозможно.

Аналогичным образом, не существует паркетов из треугольников, в каждой вершине которых сходится восемь или более сторон.

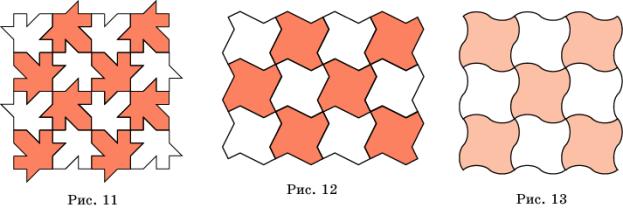
Из рассмотренных выше правильных паркетов из треугольников, квадратов и шестиугольников можно получать и другие паркеты. Например, на рисунках 11 – 13 показаны паркеты, полученные из квадратного паркета.

Самостоятельно получите новые паркеты из треугольного и шестиугольного паркетов.

Расширим способы составления паркетов из правильных многоугольников, разрешив использовать в них правильные многоугольники с различным числом сторон. Это, так называемые, полуправильные паркеты.

Паркет называется полуправильным, если он состоит из правильных многоугольников (возможно с разным числом сторон), одинаково расположенных вокруг каждой вершины.

Обозначим через ₁, ₂, … углы правильных многоугольников, имеющих общую вершину. Расположим их в порядке возрастания ₁ ₂ … . Учитывая, что сумма всех таких углов должна быть равна 360 , составим таблицу, содержащую возможные наборы углов, и укажем соответствующие паркеты.

₁

₂

₃

₄

₅

₆

₁+ ₂+…=360

Правильный паркет из 3-ов (рис. 4)

120

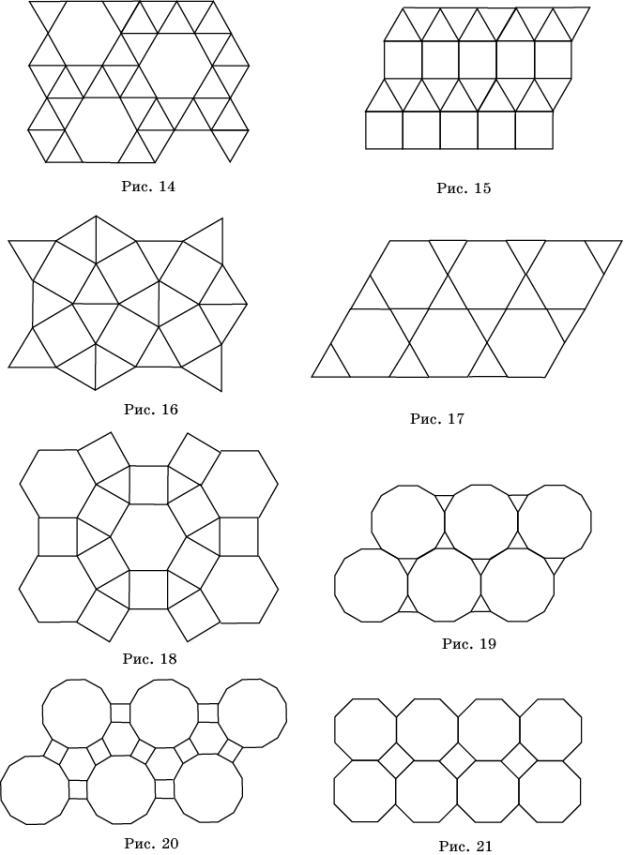
Паркет из 3-ов и 6-ов (рис. 14)

Два паркета из 3-в и 4-в (рис. 15, 16)

150

120

Паркет из 3-в и 6-в (рис. 17)

120

Паркет из 3-в, 4-в и 6-в (рис. 18)

150

Паркет из 3-в и 12-в (рис. 19)

Правильный паркет из квадратов (рис. 5)

120

150

Паркет из 4-в, 6-в и 12-в

135

Паркет из 4-в и 8-в (рис. 21)

120

Правильный паркет из 6-ов (рис. 6)

Таким образом, всего имеется 8 типов полуправильных паркетов.

Для числа этих паркетов также существенным являются не величины углов и сторон, а число сторон в многоугольниках и вершинах.

Рассмотрим теперь вопрос о заполнении плоскости неправильными равными многоугольниками.

Теорема. Для любого четырехугольника существует паркет, состоящий из четырехугольников, равных исходному. Иначе говоря, четырехугольником произвольной формы можно заполнить всю плоскость.

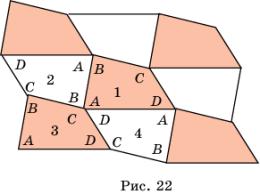
Доказательство. Пусть дан четырехугольник АВС D (рис. 22). Рассмотрим центрально-симметричный ему четырехугольник относительно середины стороны АВ. Исходный четырехугольник АВС D обозначим цифрой 1, а симметричный — цифрой 2. Теперь четырехугольник 2 отразим симметрично относительно середины его стороны ВС. Полученный четырехугольник обозначим цифрой 3 и отразим его симметрично относительно середины его стороны CD . Полученный четырехугольник обозначим цифрой 4. Четырехугольники 1, 2, 3 и 4 примыкают к общей вершине углами А, В, С и D . Поскольку сумма углов четырехугольника равна 360 , то эти четырехугольники заполнят часть плоскости вокруг общей вершины. Такое же построение можно провести вокруг каждой новой вершины, что и даст искомое заполнение плоскости.

Заметим, что четырехугольники, закрашенные одним цветом (рис. 22), получаются друг из друга параллельным переносом.

Самостоятельно составьте паркет из равных невыпуклых четырехугольников.

Паркеты из неправильных многоугольников можно получить из полуправильных паркетов, используя двойственность.

Двойственным к паркету, состоящему из правильных многоугольников, называется паркет, вершины которого находятся в центрах многоугольников данного паркета.

Ясно, что двойственным к правильному паркету, состоящему из треугольников, является правильный паркет, состоящий из шестиугольников. Двойственным к правильному паркету, состоящему из шестиугольников, является правильный паркет, состоящий из треугольников. Правильный паркет, состоящий из квадратов, двойственен сам себе.

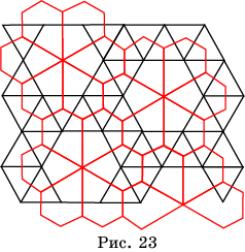
На рисунке 23 представлен паркет, состоящий из пятиугольников, двойственный паркету, изображенному на рисунке 14.

1. Можно ли составить паркет из правильных: а) пятиугольников; б) шестиугольников; в) семиугольников?

2. Можно ли составить паркет из правильных: а) восьмиугольников и четырехугольников; б) двенадцатиугольников и треугольников; в) десятиугольников и пятиугольников?

3. Можно ли составить паркет из равных треугольников произвольной формы?

4. Можно ли составить паркет из равных четырехугольников произвольной формы?

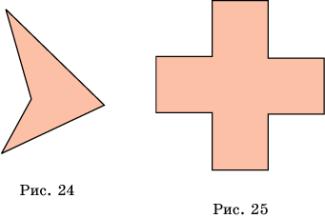
5. Нарисуйте паркет, составленный из четырехугольников, равных четырехугольнику, изображенному на рисунке 24.

6. Можно ли составить паркет из равных пятиугольников?

7. Можно ли составить паркет из равных шестиугольников произвольной формы?

8. Докажите, что с помощью центрально-симметричных шестиугольников (даже невыпуклых) можно заполнить плоскость. Приведите пример соответствующего паркета.

9. Попробуйте построить паркет из семиугольников, в каждой вершине которого сходится три стороны. Возможно ли такое построение при ограничениях на стороны семиугольников?

10. Составьте паркет из греческих крестов (рис. 25).

11. Нарисуйте паркеты, двойственные к паркетам, изображенным на рисунках 15-21.

12. Докажите, что паркеты, двойственные к полуправильным паркетам, состоят из равных многоугольников. Найдите углы этих многоугольников.

13. Используя паркеты, изображенные на рисунках 14 – 21, нарисуйте паркеты, в каждой вершине которых сходится три стороны, и состоящие из равных: а) пятиугольников, шестиугольников и двенадцатиугольников; б) пятиугольников, шестиугольников и восьмиугольников; в) четырехугольников, шестиугольников, восьмиугольников и двенадцатиугольников; г) треугольников, восьмиугольников и шестнадцатиугольников.

14. Два равных выпуклых четырехугольника разрезали: первый — по одной диагонали, а второй — по другой диагонали. Докажите, что из полученных четырехугольников можно сложить параллелограмм.

15. Выпуклый четырехугольник разрезали на четыре части по отрезкам, соединяющим середины его противоположных сторон. Докажите, что из этих частей можно сложить параллелограмм.

16. Придумайте паркеты, составленные из равных фигур, ограниченных кривыми линиями.

17. Найдите какие-нибудь условия на криволинейный четырехугольник, при которых из него можно составить паркет.

18. Выясните, как паркет на рисунке 3 может быть получен искривлением сторон паркета из четырехугольников.

19. Какое наименьшее число красок потребуется для раскраски правильных паркетов так, чтобы соседние многоугольники были окрашены в разные цвета?

20. Какое наименьшее число красок потребуется для раскраски полуправильных паркетов так, чтобы соседние многоугольники были окрашены в разные цвета?

2. Паркеты на плоскости Лобачевского

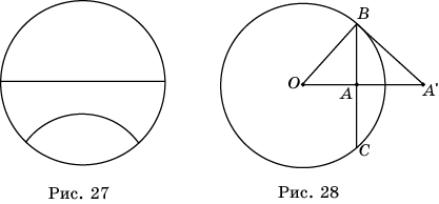
Несколько картин Мариуса Эшера посвящены паркетам на модели Пуанкаре плоскости Лобачевского (рис. 26). Будем для краткости называть ее плоскостью Лобачевского. Точками этой плоскости являются точки, расположенные внутри некоторого фиксированного круга, а прямыми – диаметры без концов и дуги окружностей (рис. 27), лежащих внутри этого круга и перпендикулярные его окружности. (Углом между двумя пересекающимися окружностями называется угол между касательными, проведенными в точке их пересечения.) Для того, чтобы определить равенство фигур на этой плоскости, напомним определение и свойства инверсии.

Инверсией относительно данной окружности с центром O и радиусом R называется преобразование, при котором точкам A плоскости, отличным от O сопоставляются точки A ’ на луче OA такие, что OA OA ’= R 2 . Точке O ничего не сопоставляется. (Иногда точке O сопоставляют бесконечно удаленную точку.)

Ясно, что если точка A принадлежит окружности, OA = R , то OA ’ = R и, следовательно, точка A переходит сама в себя.

Если точка A лежит внутри круга, OA R , то OA ’ > R и, следовательно, точка A переходит в точку вне круга.

Если точка A лежит вне круга, OA > R , то OA ’ R и, следовательно, точка A переходит в точку внутри круга.

Если точка A при инверсии переходит в точку A ’ , то точка A ’ при этой же инверсии переходит в точку A .

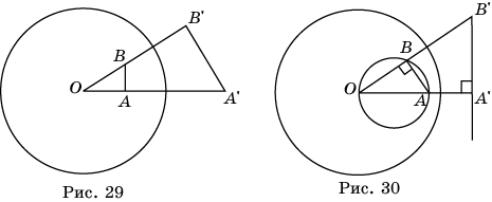
Пусть точка A лежит внутри данного круга с центром в точке O и радиусом R (рис. 28). Построим точку A ’ , в которую переходит точка A при инверсии. Для этого через точку A проведем хорду BC , перпендикулярную OA . Через точку B проведем касательную к окружности. Точка пересечения этой касательной с лучом OA будет искомой точкой A ’ . Действительно, треугольники OAB и OBA ’ подобны. Поэтому Следовательно, OA OA ’ = R 2 .

Инверсию относительно окружности можно рассматривать как аналог симметрии относительно прямой на плоскости. При симметрии относительно прямой полуплоскости меняются местами, а при инверсии относительно окружности меняются местами внутренняя и внешняя область окружности.

Установим несколько свойств инверсии.

Свойство 1. При инверсии относительно окружности с центром в точке O точки A , B переходят в точки A ’ , B ’ такие, что треугольники OAB и OB ’ A ’ подобны.

Действительно, в этом случае OA OA ’ = R 2 = OB OB ’ (рис. 29). Следовательно, Значит, треугольники OAB и OB ’ A ’ подобны.

Свойство 2. При инверсии относительно окружности с центром в точке O окружности, проходящие через точку O (без самой точки O ), переходят в прямые, не проходящие через точку O .

Действительно, пусть OA – диаметр окружности, проходящей через точку O , B – точка, принадлежащая этой окружности (рис. 30). Тогда угол OBA равен 90 и равен углу OA ’ B ’ . Следовательно, точка B ’ принадлежит прямой, проходящей через точку A ’ и перпендикулярной OA .

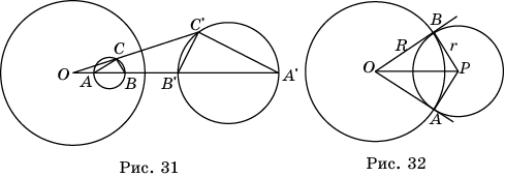
Свойство 3. При инверсии относительно окружности с центром в точке O окружности, не проходящие через точку O , переходят в окружности, не проходящие через точку O .

Действительно, пусть AB – диаметр окружности, не проходящей через точку O . Точка C принадлежит этой окружности (рис. 31). Тогда OCA = OA ’ C ’ , OCB = OB ’ C ’ . Следовательно, A ’ C ’ B ’ = OB ’ C ’ — OA ’ C ’ = OCB — OCA = ACB = 90 . Значит, точка C ’ будет принадлежать окружности с диаметром A ’ B ’ .

Свойство 4. При инверсии относительно окружности с центром в точке O окружности, перпендикулярные данной окружности, переходят сами в себя.

Действительно, пусть окружность пересекает данную окружность в точках A и B и образует с ней прямые углы (рис. 32). Тогда прямые OA и OB являются касательными к этой окружности. При инверсии окружность перейдет в окружность с теми же самыми касательными в точках A и B , т.е. в ту же самую окружность.

Заметим, что две окружности с центрами O , P и радиусами R , r перпендикулярны (рис. 32), если углы OAP и OBP – прямые. Значит, расстояние OP между центрами перпендикулярных окружностей равно .

Для плоскости Лобачевского будем называть симметрией инверсию относительно окружности, перпендикулярной данной. Кроме таких симметрий имеются еще и симметрии относительно прямых, проходящих через центр данной окружности.

Две фигуры на плоскости Лобачевского называются равными, если одну из них можно перевести в другую с помощью последовательного применения одной или нескольких симметрий.

Правильным многоугольником называется многоугольник, у которого равны все стороны и углы.

В отличие от обычной плоскости, на плоскости Лобачевского углы правильного n -угольника не равны , а могут принимать любые значения, большие нуля и меньшие .

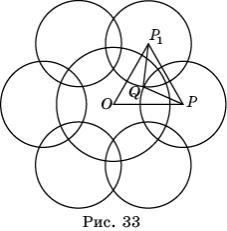
Построим, например, правильный шестиугольник. Пусть дана окружность с центром O и радиусом R , ограничивающая плоскость Лобачевского. Будем называть ее окружностью Лобачевского. Проведем какую-нибудь окружность с центром P и радиусом r , пересекающую данную окружность и такую, что угол AOB больше 60 . Будем называть ее производящей окружностью. Поворачивая эту окружность вокруг центра O на углы, кратные 60 , получим шесть окружностей, дуги которых, расположенные внутри исходной окружности, ограничивают искомый правильный шестиугольник (рис. 33).

Выясним, какие углы имеет этот правильный шестиугольник. Напомним, что угол между двумя окружностями равен углу между касательными, проведенными в точке пересечения этих окружностей. Как не трудно видеть, угол между окружностями с центрами в точках P и P ₁ равен углу PQP ₁ (рис. 33). Имеем, OP = OP ₁ = , QP = QP ₁ = r . Так как угол POP ₁ равен 60 , то треугольник POP ₁ – равносторонний и, следовательно, PP ₁ = . С другой стороны, по теореме косинусов, PP ₁ 2 = QP 2 + QP ₁ 2 – 2 QP QP ₁ cos PQP ₁ = 2 r 2 – 2 r 2 cos PQP ₁ . Из равенства R 2 + r 2 = 2 r 2 – 2 r 2 cos PQP ₁ получаем

В частности, если R = r , то угол построенного правильного шестиугольника будет равен 90 .

Паркетом на плоскости Лобачевского называется такое ее заполнение многоугольниками, при котором любые два многоугольника либо имеют общую сторону, либо имеют общую вершину, либо не имеют общих точек.

Паркет называется правильным, если он состоит из равных правильных многоугольников.

Из сказанного выше следует, что в каждой вершине правильного паркета на плоскости Лобачевского может сходиться любое число правильных треугольников, большее шести; любое число правильных четырехугольников, большее четырех; любое число правильных пятиугольников, большее трех и т.д.

Таким образом, на плоскости Лобачевского имеется бесконечно много правильных паркетов из треугольников, четырехугольников, пятиугольников и т.д.

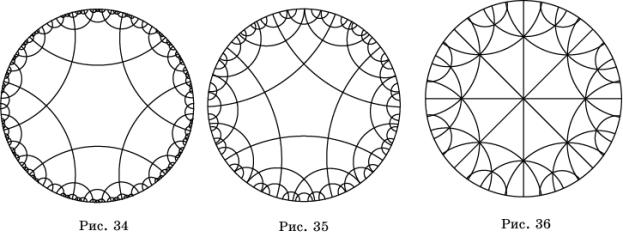
На рисунке 34 показан паркет из правильных шестиугольников. В каждой его вершине сходится четыре шестиугольника. Сначала был нарисован центральный правильный шестиугольник с углами при вершинах 90 . Другие правильные шестиугольники искомого паркета были получены из построенного правильного шестиугольника симметриями плоскости Лобачевского.Для плоскости Лобачевского будем называть симметрией инверсию относительно окружности, перпендикулярной данной. Кроме таких симметрий имеются еще и симметрии относительно прямых, проходящих через центр данной окружности.

На рисунке 35 показан паркет из правильных пятиугольников. В каждой его вершине сходится четыре пятиугольника. Сначала был нарисован центральный правильный пятиугольник с углами при вершинах 90 . Остальные пятиугольники были получены из него симметриями плоскости Лобачевского.

На рисунке 36 показан паркет из правильных треугольников. В каждой его вершине сходится восемь треугольников с углами при вершинах 45 .

1. Выясните, куда при инверсии относительно окружности с центром в точке O переходят прямые, проходящие через точку O .

2. При инверсии окружность перешла в окружность. Перешел ли: а) центр окружности в центр окружности; б) диаметр окружности в диаметр окружности?

3. На каком расстоянии от центра O окружности радиуса R должен находиться центр P окружности радиуса r , чтобы при инверсии относительно первой окружности вторая окружность переходила сама в себя?

4. Постройте прямую, проходящую через две данные точки A и B на плоскости Лобачевского (рис. 37).

5. Для данных прямых a и b на плоскости Лобачевского (рис. 38 а, б) постройте прямую b ’ , симметричную b относительно прямой a .

6. Для данных прямых a и b на плоскости Лобачевского (рис. 38 а, б) укажите симметрию, переводящую прямую a в прямую b .

7. Для данного отрезка OA на прямой a (рис. 39 а, б) постройте отрезки OB = 2 OA , OC = 3 OA .

8. Для данных точек O и A на прямой a (рис. 39 а, б) укажите симметрию, переводящую прямую a в себя и точку O – в точку A .

9. Определите понятие поворота на плоскости Лобачевского. Докажите, что поворот переводит фигуры на плоскости Лобачевского в равные им фигуры.

10. Докажите, что симметрия на плоскости Лобачевского сохраняет углы, т.е. если угол между прямыми a и b равен , то угол между прямыми a ’ и b ’ , симметричными a и b относительно некоторой прямой c , также равен .

11. Какие фигуры образуют окружности на плоскости Лобачевского?

12. Приведите пример треугольника на плоскости Лобачевского, около которого нельзя описать окружность.

13. Докажите, что около любого правильного многоугольника на плоскости Лобачевского можно описать окружность.

14. Объясните, как на плоскости Лобачевского можно построить правильный треугольник: а) с центром в центре плоскости Лобачевского; б) в вершиной в центре плоскости Лобачевского.

15. Объясните, как на плоскости Лобачевского можно построить правильный: а) четырехугольник; б) пятиугольник; в) восьмиугольник с центром в центре плоскости Лобачевского. Какого радиуса следует взять производящую окружность, и каким должно быть расстояние от ее центра до центра окружности Лобачевского, чтобы углы указанных правильных многоугольников были равны 90 ?

16. Из любого ли треугольника на плоскости Лобачевского можно составить паркет?

17. В каком случае из правильного треугольника на плоскости Лобачевского можно составить паркет?

18. Можно ли на плоскости Лобачевского составить паркет из правильных треугольников, в каждой вершине которого сходится: а) четыре стороны; б) пять сторон; в) шесть сторон; г) семь сторон?

19. Можно ли составить паркет из треугольников, равных данному треугольнику с углами 30 , 45 , 60 ?

20. Составьте паркет из какого-нибудь неправильного треугольника.

21. Выясните, каким условиям должны удовлетворять углы треугольника на плоскости Лобачевского, чтобы из него можно было составить паркет.

22. Можно ли на плоскости Лобачевского составить паркет из правильных четырехугольников, в каждой вершине которого сходится: а) четыре стороны; б) пять сторон; в) шесть сторон; г) семь сторон?

23. Составьте паркет из правильных четырехугольников, в каждой вершине которого сходится восемь сторон.

24. Выясните, каким условиям должны удовлетворять углы четырехугольника на плоскости Лобачевского, чтобы из него можно было составить паркет.

25. Составьте паркет из правильных восьмиугольников, в каждой вершине которого сходится четыре стороны.

26. Определите понятие полуправильного паркета на плоскости Лобачевского. Приведите пример.

27. Определите понятие двойственного паркета. Приведите пример.

28. Образуют ли дуги окружностей на рисунке 26 полуправильный паркет на плоскости Лобачевского?

29. Какое наименьшее число красок потребуется для раскраски паркетов на рисунках 34 – 36 так, чтобы соседние многоугольники были окрашены в разные цвета?

30. Для окружности на координатной плоскости, заданной уравнением x 2 + y 2 = R 2 , и точки A ( x ₀ , y ₀ ), найдите координаты точки A ’ , полученной из точки A инверсией относительно данной окружности.

31. Используя координатный метод, докажите, что при инверсии относительно окружности с центром в точке O (0, 0) окружности, не проходящие через точку O , переходят в окружности, не проходящие через точку O , а окружности, проходящие через точку O (без самой точки O ), переходят в прямые, не проходящие через точку O .

3. Паркеты на сфере

Напомним, что аналогом многоугольника на сфере является фигура, ограниченная дугами больших окружностей. Мы будем называть такие фигуры сферическими многоугольниками, а соответствующие дуги больших окружностей – сторонами. Легко видеть, что сферический многоугольник может быть получен как пересечение сферы и многогранного угла с вершиной в центре этой сферы. Сферический многоугольник называется правильным, если равны все его стороны и углы.

Паркетом на сфере называется такое заполнение сферы сферическими многоугольниками, при котором любые два сферических многоугольника либо имеют общую сторону, либо имеют общую вершину, либо не имеют общих точек.

Паркет на сфере называется правильным, если он состоит из равных правильных сферических многоугольников.

Паркет на сфере называется полуправильным, если он состоит из правильных сферических многоугольников (возможно, с разным числом сторон) и для любых его вершин существует движение сферы, переводящее паркет сам в себя и одну из данных вершин в другую.

Отметим связь правильных и полуправильных паркетов на сфере с правильными и полуправильными многогранниками.

Напомним, что выпуклый многогранник называется правильным, если его гранями являются равные правильные многоугольники и в каждой вершине сходится одинаковое число ребер.

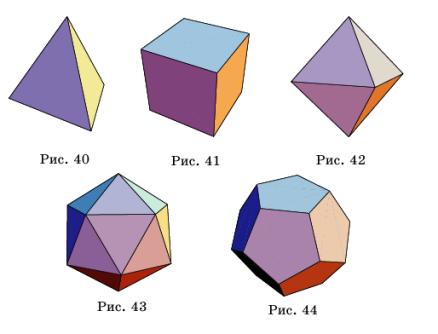
Имеется пять типов правильных многогранников: тетраэдр, его гранями являются четыре правильных треугольника (рис. 40); гексаэдр ( куб) – многогранник, гранями которого являются шесть квадратов (рис. 41); октаэдр, его гранями являются восемь правильных треугольников (рис. 42); икосаэдр, его гранями являются двадцать правильных треугольников (рис. 43); додекаэдр, его гранями являются двенадцать правильных пятиугольников (рис. 44).

Полуправильным многогранником называется выпуклый многогранник, гранями которого являются правильные многоугольники, возможно, и с разным числом сторон, и для любых двух вершин существует движение, переводящее многогранник сам в себя и одну из данных вершин в другую.

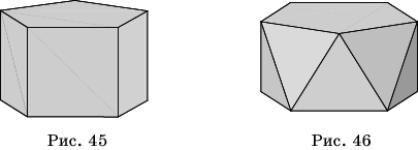
К полуправильным многогранникам относятся правильные призмы, все ребра которых равны. Например, правильная шестиугольная призма на рисунке 45 имеет своими гранями два правильных шестиугольника — основания призмы, и шесть квадратов, образующих боковую поверхность призмы. К полуправильным многогранникам относятся и, так называемые, антипризмы с равными ребрами. На рисунке 46 мы видим пятиугольную антипризму, полученную из пятиугольной призмы поворотом одного из оснований относительно другого на угол 36 . Каждая вершина верхнего и нижнего оснований соединена с двумя ближайшими вершинами другого основания.

Кроме этих двух бесконечных серий полуправильных многогранников, имеется еще 13 полуправильных многогранников, которые впервые открыл и описал Архимед — это тела Архимеда.

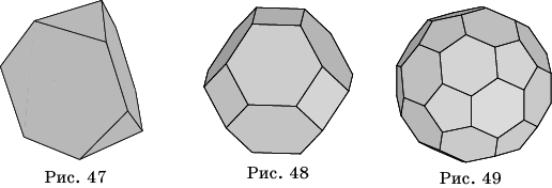
Самые простые из них получаются из правильных многогранников операцией «усечения», состоящей в отсечении плоскостями углов многогранника. Если срезать углы тетраэдра плоскостями, каждая из которых отсекает третью часть его ребер, выходящих из одной вершины, то получим усеченный тетраэдр, имеющий восемь граней (рис. 47). Из них четыре — правильные шестиугольники, и четыре — правильные треугольники. В каждой вершине этого многогранника сходятся три грани.

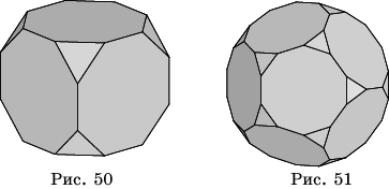
Если указанным образом срезать вершины октаэдра и икосаэдра, то получим соответственно усеченный октаэдр (рис. 48) и усеченный икосаэдр (рис. 49). Обратите внимание на то, что поверхность футбольного мяча изготавливают в форме поверхности усеченного икосаэдра. Из куба и додекаэдра также можно получить усеченный куб (рис. 50) и усеченный додекаэдр (рис. 51).

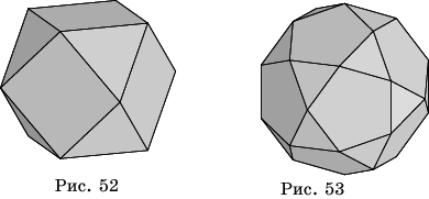
Для того чтобы получить еще один полуправильный многогранник, проведем в кубе отсекающие плоскости через середины ребер, выходящих из одной вершины. В результате получим полуправильный многогранник, который называется кубооктаэдром (рис. 52). Его гранями являются шесть квадратов, как у куба, и восемь правильных треугольников, как у октаэдра. Отсюда и его название — кубооктаэдр.

Аналогично, если в додекаэдре отсекающие плоскости провести через середины ребер, выходящих из одной вершины, то получим многогранник, который называется икосододекаэдром (рис. 53). У него двадцать граней — правильные треугольники, и двенадцать граней — правильные пятиугольники, т.е. все грани икосаэдра и додекаэдра.

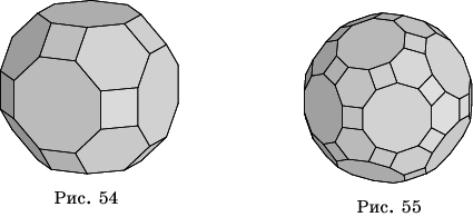
Следующие два многогранника называются усеченный кубооктаэдр (рис. 54) и усеченный икосододекаэдр (рис. 55). Однако они не получаются операцией «усечения» из кубооктаэдра и икосододекаэдра, соответственно. Действительно, если в кубооктаэдре и икосододекаэдре провести отсекающие плоскости, то в сечениях получатся прямоугольники, а не квадраты, как требуется.

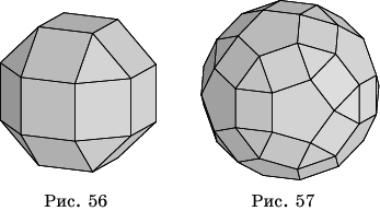
На рисунке 56 изображен ромбокубооктаэдр. Он состоит из граней куба и октаэдра, к которым добавлены еще 12 квадратов.

На рисунке 57 изображен ромбоикосододекаэдр, состоящий из граней икосаэдра, додекаэдра и еще 30 квадратов.

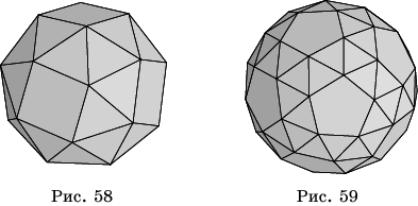
На рисунках 58 и 59 представлены соответственно, так называемые, плосконосый (иногда называют курносый) куб и плосконосый ( курносый) додекаэдр, которые состоят из граней куба или додекаэдра, окруженных правильными треугольниками.

Легко видеть, что каждому паркету на сфере, состоящему из правильных сферических многоугольников, можно сопоставить многогранник, вершинами которого будут вершины этого паркета. При этом правильному паркету на сфере соответствует правильный многогранник, а полуправильному паркету – полуправильный многогранник. Наоборот, каждому правильному и полуправильному многограннику можно сопоставить паркет на сфере, описанной около этого многогранника, вершинами которого будут вершины этого многогранника. При этом правильному многограннику соответствует правильный паркет на сфере, а полуправильному многограннику – полуправильный паркет.

Имеется взаимнооднозначное соответствие между правильными и полуправильными паркетами на сфере и правильными и полуправильными многогранниками. Таким образом, на сфере имеется пять правильных паркетов, соответствующих правильным многогранникам; две бесконечные серии полуправильных паркетов, соответствующих призмам и антипризмам, и 13 полуправильных паркетов, соответствующих телам Архимеда.

Также как и на плоскости, наличие только пяти типов правильных паркетов на сфере обусловлено не величинами углов правильных сферических многоугольников, а более общими топологическими свойствами сферы.

Топология – раздел геометрии, изучающий свойства фигур, не меняющиеся при непрерывных деформациях, включающих в себя растяжения, сжатия, изгибания и т.п. Две фигуры называются топологически эквивалентными, если одна из них получается из другой с помощью непрерывной деформации. Так, например, все n -угольники топологически эквивалентны, все простые замкнутые линии на плоскости топологически эквивалентны окружности.

Рассмотрим паркеты на сфере, образованные криволинейными многоугольниками. Паркет называется топологически правильным, если он состоит из одноименных многоугольников и в каждой вершине сходится одинаковое число сторон. Докажем, что существует только пять типов топологически правильных паркетов на сфере, которые соответствуют правильным многогранникам. Для этого воспользуемся теоремой Эйлера о числе вершин (В), ребер (Р) и граней (Г) выпуклого многогранника, переформулированной на язык паркетов.

Теорема. Для любого паркета на сфере выполняется следующее равенство:

где В – число вершин, Р – число сторон (ребер), Г – число многоугольников (граней) данного паркета.

Доказательство. Для данного паркета рассмотрим какую-нибудь его сторону (ребро), соединяющую две вершины. Стянем ее вместе с вершинами в одну точку. При этом число вершин уменьшится на единицу (вместо двух вершин стала одна), число ребер уменьшится на единицу, число граней не изменится. Следовательно, В – Р + Г при этом не изменится. Будем последовательно стягивать ребра, соединяющие различные вершины, пока не останется одна вершина, а стороны превратятся в петли с началом и концом в данной вершине. При этом В – Р + Г будет таким же, как и у исходного паркета. Уберем одно из ребер — петель. При этом число вершин не изменится, число ребер уменьшится на единицу, число граней уменьшится на единицу (две грани соединятся в одну). Следовательно, В – Р + Г при этом не изменится. Будем последовательно убирать ребра, пока не останется одно ребро. В результате В – Р + Г будет таким же, как у исходного паркета. При этом В = 1, Р = 1, Г = 2, т.е. В – Р + Г = 2. Значит, равенство В – Р + Г = 2 справедливо и для исходного паркета.

Теорема. На сфере существует только пять типов топологически правильных паркетов.

Доказательство. Пусть дан топологически правильный паркет на сфере, составленный из n -угольников, и в каждой вершине сходится m сторон. Ясно, что n и m больше или равны трем. Обозначим, как и раньше, В — число вершин, Р — число сторон (ребер) и Г — число многоугольников (граней) этого паркета. Тогда

Г n = 2P; Г = ; B m = 2P; В = .

По теореме Эйлера В — Р + Г = 2 и, следовательно,

Откуда Р = . Из полученного равенства, в частности, следует, что должно выполняться неравенство 2 n + 2 m – nm > 0, которое эквивалентно неравенству ( n – 2)( m – 2)

Найдем всевозможные значения n и m , удовлетворяющие найденному неравенству, и заполним следующую таблицу.

Содержание

Геометрические паркеты
Геометрические паркеты
Паркеты из одинаковых правильных многоугольников
Паркеты из разных правильных многоугольников
Паркеты из неправильных многоугольников
Паркеты из произвольных фигур
Исследовательская работа по математике » Геометрические паркеты»
🔥 Видео

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Геометрические паркеты

Видео:32 Четыре паркета, или Отражения треугольника относительно его сторонСкачать

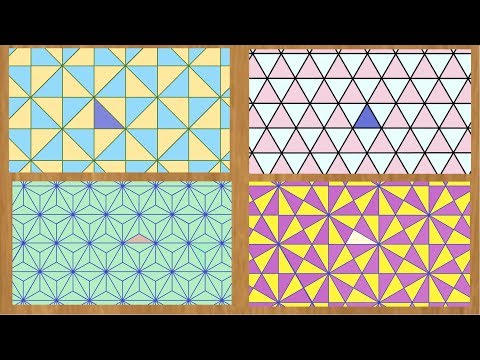
Геометрические паркеты

Паркет (или мозаика) — бесконечное семейство многоугольников, покрывающее плоскость без просветов и двойных покрытий. Иногда паркетом называют покрытие плоскости правильными многоугольниками, при котором два многоугольника имеют либо общую сторону, либо общую вершину, либо совсем не имеют общих точек; но мы будем рассматривать как правильные, так и неправильные многоугольники. Итак, какими же многоугольниками можно замостить плоскость?

Паркеты из одинаковых правильных многоугольников

Сумма всех углов n-угольника равна 180°(n-2). Все углы правильного многоугольника равны; следовательно, каждый из них равен 180°(n-2)/n. В каждой вершине паркета сходится целое число углов; поэтому число 2·180° должно быть целым кратным числа 180°(n-2)/n. Преобразуем отношение этих чисел:

Разность n-2 может принимать лишь значения 1, 2 или 4; поэтому n может быть равно только 3, 4 или 6. Значит, можно получить паркеты, составленные из правильных треугольников, квадратов или правильных шестиугольников.

Паркеты из разных правильных многоугольников

Сначала выясним, какое количество различных правильных многоугольников (с одинаковыми длинами сторон) может находиться вокруг каждой точки. Величина угла правильного многоугольника должна находиться в интервале от 60° до 180° (не включая); следовательно, число многоугольников, находящихся в окрестности точки, должно быть больше 2 (360°/180°) и не может превышать 6 (360°/60°).

Можно показать, что существуют следующие способы уложить паркет комбинациями правильных многоугольников: (3,12,12); (4,6,12); (6,6,6); (3,3,6,6) — два варианта паркета; (3,4,4,6) — четыре варианта; (3,3,3,4,4) — четыре варианта; (3,3,3,3,6); (3,3,3,3,3,3) (цифры в скобках — обозначения многоугольников, сходящихся в каждой вершине: 3 — правильный треугольник, 4 — квадрат, 6 — правильный шестиугольник, 12 — правильный двенадцатиугольник). Некоторые варианты паркета показаны на следующих иллюстрациях:

Остальные варианты паркетов, а также доказательство того, что не существует других вариантов укладки паркета из правильных многоугольников (при условии, что любые два многоугольника в паркете имеют либо общую сторону, либо общую вершину, либо совсем не имеют общих точек), см. в статье и др. «Геометрический паркет на экране компьютера» (статья — в виде картинок на двух страницах, объем каждой страницы порядка 500 кб; источник — журнал «Информатика и образование, №9 за 2002 г.).

Паркеты из неправильных многоугольников

Легко покрыть плоскость параллелограммами:

Вообще можно замостить плоскость копиями произвольного четырехугольника, необязательно выпуклого:

Можно составить паркет из копий произвольного треугольника: из двух равных треугольников можно сложить параллелограмм, и покрыть плоскость копиями этого параллелограмма.

Еще плоскость можно покрыть копиями центрально-симметричного шестиугольника, или копиями пятиугольника с двумя параллельными сторонами. До сих пор не найдены все типы выпуклых пятиугольников, из которых складываются паркеты. Зато доказана теорема, утверждающая: «Нельзя сложить паркет из копий выпуклого семиугольника». В то же время существуют паркеты из невыпуклых семиугольников:

Паркеты из произвольных фигур

Некоторые определения паркета не ограничиваются многоугольниками; в этом случае паркетом называется покрытие плоскости без пропусков и перекрытий заданными фигурами (в частном случае — многоугольниками, правильными или неправильными, выпуклыми или невыпуклыми). В таком случае даже для паркетов из многоугольников может не соблюдаться требование «два многоугольника должны иметь общую вершину, общую сторону или совсем не иметь общих точек»; кроме того, появляется множество разнообразных паркетов, состоящих не из многоугольников, а из криволинейных фигур. Рассмотрим способы построения нового паркета, исходя из этого «расширенного» определения. Итак, как нарисовать паркет? (некоторые из возможных способов)

Способ первый. Берем некоторую сетку (уже известный нам паркет) — из правильных треугольников, шестиугольников, квадратов, или из произвольных многоугольников, и выполняем преобразования: сжатие/растяжение, замена прямолинейных отрезков кривыми с началом и концом в тех же точках, что и у отрезков.
Пример: паркеты, полученные заменой отрезков «квадратной» сетки некоторыми кривыми или ломаными.

Способ второй. Объединяем отдельные элементы уже существующих паркетов. Примеры: паркеты, полученные в результате объединения элементов квадратной сетки:

Паркет, каждый элемент которого получен в результате объединения пяти правильных треугольников:

Способ третий. Берем существующую сетку и дополняем ее новыми линиями. Получаем разбиение плоскости на фигуры, которые затем можно по-новому объединить. В частном случае — накладываем друг на друга две (или более) сетки уже известных паркетов, смещая или поворачивая одну сетку относительно другой; фигуры, образовавшиеся при пересечении линий, считаем элементами паркета.
Пример (разбиения сетки из греческих крестов):

Способ четвертый. Выбираем некоторую кривую или ломаную и начинаем ее переносить на некоторый вектор, поворачивать, отражать. получившиеся кривые или ломаные размещаем на плоскости таким образом, чтобы они образовали замкнутые контуры (которые в дальнейшем будут рассматриваться как элементы паркета). Если рассматривать только незамкнутые кривые и ломаные, паркеты будут напоминать полученные способом №1.
Для получения следующего паркета была взята дуга спирали, три раза повернута на 90°, а затем к получившейся фигуре был применен параллельный перенос.

А вот паркеты, полученные с помощью параллельного переноса звездчатых многоугольников:

Совмещая вершины звездчатых многоугольников, получаем паркеты, состоящие из правильных восьмиугольников, равнобедренных прямоугольных треугольников, а также из невыпуклых 16-угольников, напоминающих крест. На первом рисунке есть еще один элемент — выпуклый четырехугольник.

Источники:
. Паркеты из правильных многоугольников. Журнал «Квант» №3, 1970 г. . Паркеты. , , . Геометрический паркет на экране компьютера. Журнал «Информатика и образование», 9-2002.

Также при подготовке страницы были использованы материалы, подготовленные мной для УМК «Геометрические паркеты» («Как нарисовать паркет, или почему не бывает тетрадей в кружочек»).

См. также: Одиннадцать правильных паркетов на сайте Арбуз

Видео:Мозаика Пенроуза, бесконечная и неповторимая [Veritasium]Скачать

Исследовательская работа по математике » Геометрические паркеты»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Паркеты с древних времен привлекали к себе внимание людей. Паркеты являются своеобразными орнаментами. Над созданием паркетов – орнаментов трудились многие поколения мастеров, подчас создавая истинные шедевры красоты.

Тема «Паркеты» актуальна и в наши дни. Паркетами покрывают полы в домах, украшают стены комнат и зданий Каждому из нас хочется, чтобы было не только прочно, но оригинально и красиво, поэтому без многоугольников ни один дизайнер не обойдется, ни один человек, который собирается сделать ремонт.

С паркетами мы встречаемся в повседневной жизни. Тетрадный лист в клеточку представляет собой простейший паркет. Элементом паркета здесь является квадрат. Можно придумать сотни, тысячи разных элементов паркета.

В моей работе я буду рассматривать геометрические паркеты из многоугольников.

Цель и задачи проектной работы.

1.Расширение теоретической базы, аналитический обзор литературы по теме.

2.Изучить геометрические приёмы составления паркетов.

3. Научиться строить паркеты с помощью графического редактора « Paint », входящего в стандартный пакет Microsoft Office .

4.Развитие умений и навыков исследовательской работы.

Выдвинута проблема. Какими правильными многоугольниками можно замостить плоскость?

Объект исследования — паркеты.

Методы исследования: анализ литературы; систематизация материала; метод аналогии.

При работе над проектом я пользовалась материалом из книг, журналов, использовала Интернет — ресурсы.

1. Историческая справка.

Слово «паркет» имеет благородное французское происхождение. Однако в средние века во Франции им обозначали небольшой парк, немного спустя — предназначенную для аудиенций часть зала, покрытую ковром. Ковры постепенно исчезли, паркетные полы стали частью интерьера, так же искусно выполненной, как настенные гобелены.

Русский паркет, насчитывающий несколько сот лет своего существования и имевший самые разнообразные формы, прошел длительный путь своего развития. В России паркетные полы были нововведением Петра I., который привез целый цех краснодеревщиков с Запада, в частности, из Германии. Полы в русских постройках, начиная со времен Петра, приобрели иной, художественный, вид. Ассортимент деревьев, употребляемых для паркета, увеличивался, и наряду с местными отечественными породами: березой, орехом, сосной, лиственницей, кленом, дубом, буком, грабом, ясенем, вязом, грушей, яблоней, ольхой, можжевельником, карагачем и кизилем — стали все более и более применять редкие и дорогостоящие сорта привозных «заморских» деревьев. В зависимости от употребляемых материалов паркеты носили различные названия: цветные (т. е. набранные из привозных деревьев), полуцветные, штучные (набранные из местных пород) и дубовые.

Сейчас, в начале ХХI века, несмотря на развитие науки и техники, можно сомневаться — все ли технологические тайны старых мастеров-паркетчиков удалось восстановить. Можно сказать, что благодаря буквально нескольким мастерам — реставраторам искусство художественного паркета в нашей стране сохранилось до наших дней.

Паркет в Итальянском зале Паркет начала 18 века

Правда, технология со временем изменяется, детали орнамента и рисунка сегодня вырезаются уже не вручную, а на станках и с применением лазера и компьютера, появилось много машин, облегчающих труд.

2. Геометрические п аркеты.

П аркетом называют замощение плоскости многоугольниками, при котором вся плоскость оказывается покрытой ими без просветов и двойных покрытий. Иногда паркетом называют покрытие плоскости правильными многоугольниками, при котором два многоугольника имеют либо общую сторону, либо общую вершину, либо совсем не имеют общих точек.

2.1. Паркеты из правильных одноименных многоугольников.

1.Из каких правильных одноименных многоугольников можно составить паркет?

Предположение: правильные паркеты получатся из квадратов, шестиугольников и треугольников.

В природе и в жизни человека паркеты встречаются часто. Например: шахматная доска и пчелиные соты. Все эти предметы состоят из многоугольников с равными углами и равными сторонами. Пример шахматной доски меня убеждает, что из правильных: четырехугольников тоже можно составить правильный паркет.

На примере пчелиных сот убеждаемся, что паркет можно составить и из правильных шестиугольников. Пчелы бессознательно решают математическую задачу – они стараются придать сотам такую форму, чтобы при заданном объёме на них шло как можно меньше воска. И хотя они не знают математики, но точно решают эту задачу. Пчелам помогает решать эту задачу инстинкт.

В свою очередь, правильные шестиугольники состоят из правильных треугольников, поэтому паркеты из правильных треугольников тоже существуют

Выясним, из каких ещё правильных многоугольников можно составить паркет?

Можно ли замостить плоскость правильными пятиугольниками?

Геометрические фигуры могут «встретиться» в вершине паркета только тогда, когда сумма их углов составляет 360 градусов, иначе они не сомкнуться вокруг вершины или «налезут» друг на друга).

Итак, главное условие, необходимое для построения паркетов:

Сумма углов многоугольников в узле паркета должна равняться 360 º

Пусть в каждой точке плоскости сходятся m одинаковых правильных n -угольников, то должно выполняться равенство:

После преобразований получим:

Если n =3, m =6 (6 треугольников в узле).

Если n =4, m =4 (4 четырёхугольника в узле).

Если n =5, m =3,333333… Но m не может быть дробным числом, число многоугольников должно быть натуральное.

Значит, пятиугольниками заполнить плоскость нельзя.

Если n =6, m =3 (шестиугольника)

Для п ≥ 7 не существует правильных многоугольников, для которых бы выполнялось главное условие. Значит, паркет из этих многоугольников ( п > 7; 8; 9… ) построить нельзя!

Вывод: Наше предположение оказалось верным.

Мы убедились в том, что паркет можно построить из: