Содержание:
По этой ссылке вы найдёте полный курс лекций по математике:
Наглядный геометрический объест — плоская кривая — приточных определениях приводит к нескольким различным, хотя и близким понятиям. Плоскую кривую можно понимать и как некоторое множество точек на плоскости и как множество точек плоскости вместе с очередностью их прохождения — ориентацией. Приведем два наиболее распространенных подхода к определению того, что представля ет собой плоская кривая. Пусть на плоскости введена прямоугольная декартова система координат Оху.
- Определение 1 (неявный способ задания):
- Способы задания
- Параметризация с помощью параметризации осуществляется оценка
- Уравнение окружности в параметрическом виде
- 6. Параметрическое задание линий
- Содержание
- Параметрическое представление функции [ править | править код ]
- Параметрическое представление уравнения [ править | править код ]
- Параметрическое уравнение [ править | править код ]
- Примеры [ править | править код ]
- Уравнения некоторых кривых в параметрической форме:
- 🌟 Видео
Определение 1 (неявный способ задания):
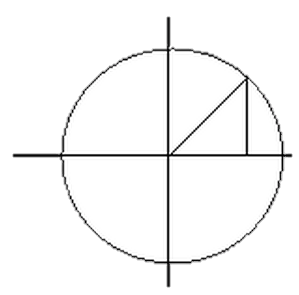
Плоской кривой называется множество 7 точек М плоскости, координаты х и у которых при подстановке в уравнение ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ Плоские кривые. Способы задания. Естественная параметризация обращают его в тождество. Пример 1 Уравнение , задает окружность радиуса а с центром в точке 0(0,0) <рис. 1).
Другим распространенным способом задания плоской кривой является параметрический способ задания. Определение 2. Параметризованной плоской кривой называется множество 7 точек М плоскости, координаты г и у которых определяются соотношениями непрерывные на отрезке [а, 6] функции. Пример 2. — параметрические уравнения окружности радиуса а с центром в точке 0(0,0). При изменении параметра t от 0 до 2т соответствующая точка обегает окружность против часовой стрелки.
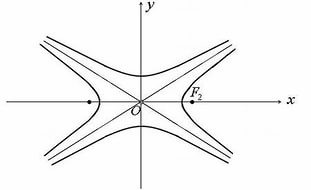
Данное определение допускает естественную физическую интерпретацию. Если воспринимать параметр t как время, то параметрически заданную кривую можно рассматривать как след движущейся точки М(х, у), координаты которой изменяются со временем по правилу (2). При этом вовсе не исключается случай, когда при своем движении переменная точка М в некоторый момент t* может вновь оказаться там, где ранее (в момент i, она уже находилась: (рис.2). Геометрически этоодна и та же точка.
Однако вследствие того, что в рассматриваемом процессе мы попадаем в нее дважды в разные моменты времени, это две разные точки кривой, задаваемой параметрическими уравнениями (2). Замечание. Строго говоря, определении I и 2 вводят в рассмотрение разные объекты. Поэтому для того, чтобы не впасть в заблуждение, нужно ясно представлять, в каком именно смысле рассматривается задаваемая кривая. Пусть кривая 7 задана параметрическими уравнениями называется начальной тонкой этой кривой, а точка ) — конечной тонкой кривой 7.
Кривая 7 называется замкнутой, если ее начальная и конечная точки совпадают (рис. 4).
— Рис. 4 Одно и то же м ножество точекн а плоскости можно задавать при помощи различных параметрических уравнений. Пример 3. Уравнения задают окружность радиуса а, обходимую в положительном направлении. Легко видеть, что, положив в формулах (3) 2хг3, мы приходим к соотношениям (4). Определение. Функция подчиненная условиям: а) Н3]; в) область значения функции h(r) — отрезок [а, Ь], называется непрерывной заменой параметра кривой 7 (рис. 5). ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ Плоские кривые.
Способы задания
Естественная параметризация Заменяя в формулах (2) параметр t на функцию Л(т), получаем уравнения — другую параметризацию кривой 7. Любую кривую можно параметризовать многими различными способами. Определение 3. Плоская кривая 7 называется п-гладкой относительно параметризации если функции ) принадлежит классу .
Если порядок п гладкости функций несуществен, то говорят просто о гладкой кривой. Пример 4. Кривая заданная уравнениями является 3-гладкой (рис. в а). Пример S. Кривая 7, заданная уравнениями является 2-гладкой. Однако множеств о точек на плоскости, описываемое этими уравнениями, имеет • точке О (при t ) особенность — излом (рис.вб). Это означает, что гладкость функций . задающих кривую, не обеспечивает плавного ее изменения.
Отметим, что производные этих функций при tодновременно обращаются а нуль. ТЪчка Мо гладкой кривой у, отвечающая значению t0 параметра, М0 в которой называется особой точкой этой кривой (относительно заданной параметризации). Точка Мо(*о) гладкой кривой 7, в которой называется обыкновенной, ншрегулярной, точкой этой кривой. Пример в. Все точки окружности (3) являются регулярными.
Пример 7. У кривой, задаваемой уравнениями (астроида) четыре особых точки (при t ж 0, | Последнее неравенство означает, что скорость кривой 7 относительно заданной параметризации не обращается в нуль ни в одной точке кривой. При изменении параметра t текущая точка M(t) перемещается порегулярной кривой 7, нигде не оста- навливаясь и не поворачивая вспять, поскольку скорость регулярной кривой ни при каких значениях параметра не обращается в нуль.
Возможно вам будут полезны данные страницы:
Пусть 7 — регулярная кривая, заданная параметрически. Обозначим через Мо точку кривой 7, отвечающую значению £о параметра, а через М — точку кривой 7, отвечающую значению t параметра из некоторой окрестности точки to (рис. 8, 9). Прямая М0Т называется касательной регулярной кривой 7 вточке Мо, если при (или, что то же, ) наименьший Д0 из углов между этой прямой и переменной прямой MqM стремится к нулю (рис. 9). Регулярная кривая имеет касательную в каждой своей точке.
Вектор скорости кривой в точке Мо коллинеарен ее ка- сательной в этой точке. Прямая, проходящая через точку Мо перпендикулярно касательной кривой 7 в этой точке, называется нормалью кривой вточке Мо. Замена параметра называется регулярной у если Л'(т во всех точках отрезка [а, /3]. В случае неявного задания (1) кривая 7 будет регулярной, если в каждой ее точке М(х, у) выполняется неравенство Точка Мо(жо> Уо) неявно заданной кривой 7 называется особой, если в этой точке Пример 8.
| Кривая, заданная уравнением |
(леммисюга Бернулт), имеет одну особую точку 0(0,0) — узел (рис.10). Различают несколько типов особых точек. Пусть М0(хо, уо) — особая точка кривой 7, Введем следующие обозначения возврата первого рода. Пример 12. (рис. 14). — точка возврата второго рода. Гладкая (тем более регулярная) кривая спрямляема. Длина кривой 7, заданной уравнениями (2), вычисляется по формуле Значение функции равно длине переменной дуги кривой7, заключенной между точками (рис. 15).
Функция на отрезке [а, 6) строго возрастает, Пример 11. ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ Плоские кривые. Способы задания. Естественная параметризация и является гладкой на отрезке [а, 6]. Кроме того, область значений функции s(t) совпадает с отрезком [0, 5]. Тем самым, длину дуги можно взять за новый, естественный (натуральный) параметр кривой.
Параметризация кривой, где в качестве параметра взята длина дуги з, называется естественной параметризацией. Если естественная параметризация кривой, то Поэтому естественно параметризованную кривую часто называют кривой с единичной скоростью. Пример 13. Параметризация окружности радиусе а является естественной:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Видео:Математический анализ 25. Натуральная параметризация кривой. Сопровождающий трёхгранникСкачать

Параметризация с помощью параметризации осуществляется оценка
| Название | Параметризация с помощью параметризации осуществляется оценка |
| Дата | 10.01.2022 |
| Размер | 30.64 Kb. |
| Формат файла |  |
| Имя файла | 1.docx |
| Тип | Документы #326937 |
| Подборка по базе: Распознавание речи с помощью CMU Sphinx.pdf, Занятие №7 Вычисление значений функции с помощью высших дифферен, Защита личных не имущественных прав супругов осуществляется по п, 2__Алгебра 10 Исследование функций с помощью производной.doc, Определение прочности с помощью Молотка Кошкарова.docx, Лабораторная работа Определение ускорения свободного падения с п, Размещение и перемещение тыла осуществляется в соответствии с оп, Категории лиц, в отношении которых осуществляется индивидуальная, Обзор исследований распознавания рукописных текстов с помощью сп, Управление транспортом с помощью нейросетей.docx Параметризация
Аксонометрия
К линейчатым поверхностям относят: Множество линий, заполняющих поверхность так, что через каждую точку поверхности в общем случае проходит одна линия этого множества, носит название: Образующая поверхность вращения может быть: Плоской и пространственной кривой. Линейчатая поверхность в общем случае однозначно определяется: Конечное множество точек, задающих поверхность, носит название: 2. Точечного каркаса. Очерк поверхности – это: 2. Проекции поверхности. В начертательной геометрии классификация поверхностей производится на основании: 2. Формы образующих и закона образования. Геликоиды – это винтовые поверхности, образующими которых являются: Поверхности, образующими которых являются прямые линии, называются: Поверхности, образующими перемещением окружности постоянного или переменного радиуса, называются: ГЧО поверхности включает: образующую прямую т и ось вращения і. Если milj, образуется поверхность К коникам НЕ относится Для однозначного задания поверхности на чертеже необходимо и достаточно решить вопрос о принадлежности поверхности произвольной Проекции каркаса могут быть построены, если задан К коникам НЕ относится К линейчатым поверхностям НЕ относится Поверхность, образованная непрерывной совокупностью замкнутых плоских сечений, определенным образом ориентированных в пространстве, носит название В процессе образования поверхности образующая НЕ может Определитель поверхности — это Набор гесметрическик фигур и алгоритм их взаимодействия Вращательно поступательным перемещением точки Плоскость, перпендикулярная оси вращения, пересекает поверхность по Поверхность, образованная непрерывной совокупностью последовательных положений некоторой линии, перемещающейся в пространстве, носит название Циклическая поверхность с образующей постоянного вида называется К линейчатым поверхностям не относятся Двуполостный гиперболоид вращения Плоскость, проходящая через ось вращения, пересекает поверхность по Поверхность, полученная вращением эллипса вокруг малой оси, называется Поверхность, образованная движением прямой т, параллельной плоскости параллелизма по двум направляющим кривым линиям, называется В НГ классификация поверхностей производится на основании Формы образующей и закона образования Коноид — поверкность, образованная движением прямолинейной образующей, параллельной плоскости Двум направляющим, кривой и прямой ГЧО поверхности включает: образующую прямую т и ось вращенияj. Если m.lj. образуется поверхность ГЧО поверхности включает: образующую прямую т и ось вращения j. Если m скрещивается с j. Образуется поверхность Геликоиды — это винтовые поверхности, образующими которых являются ГЧО поверхности включает: образующую прямую и ось вращения j. Если mnj, образуется поверхность Образующая циклической поверхности может быть Образующая винтовой поверхности может быть Прямой или кривой
Числовые отметки
начертательная геометрия
Способы преобразования проекций применяются для решения: Способы преобразования проекций применяются с целью нахождения: Истинных величин фигур и рациональных способов решения задач. Оригинал остается неподвижным относительно исходных плоскостей проекций при использовании способа: Замены плоскостей проекций. Оригинал остается неподвижным относительно исходных плоскостей проекций при использовании способа: Оригинал изменяет свое положение относительно исходных плоскостей проекций при использовании способа: Вращения вокруг линии уровня. Оригинал изменяет свое положение относительно исходных плоскостей проекций при использовании способа: 2. Плоскопараллельного перемещения. При использовании способа замены плоскостей проекций новая плоскость проекций по отношению к незаменяемой плоскости проекций располагается: При использовании способа замены плоскостей проекций расстояние от новой оси до новой проекции точки: Равно расстоянию от заменяемой оси до заменяемой проекции точки. К четырем основным задачам на преобразование можно отнести: 3. Обе названные задачи. К четырем основным задачам на преобразование можно отнести: 3. Обе названные задачи. Плоскопараллельным называется перемещение, при котором все точки оригинала перемещаются: Параллельно плоскости проекций. Плоскопараллельное перемещение возможно относительно: Любой из плоскостей проекций. Траектория движения каждой точки оригинала при плоскопараллельном перемещении относительно горизонтальной плоскости проекций находится: В горизонтальной плоскости. Траектория движения каждой точки оригинала при плоскопараллельном перемещении относительно фронтальной плоскости проекций находится: Во фронтальной плоскости. При плоскопараллельном перемещении относительно горизонтальной плоскости проекций остается равной самой себе, изменяя лишь свое положение: Горизонтальная проекция оригинала. При плоскопараллельном перемещении относительно фронтальной плоскости проекций остается равной самой себе, изменяя лишь свое положение: Фронтальная проекция оригинала. Частным случаем плоскопараллельного перемещения является способ: Плоскость вращения точки относительно оси вращения расположена: При вращении вокруг фронтально-проецирующей оси траектория точки проецируется в виде окружности на: Фронтальную плоскость проекций. В начертательной геометрии задачи на определение взаимного положения оригиналов носят название: В начертательной геометрии задачи на определение истинных величин фигур носят название: Способы преобразования проекций НЕ применяются для: Определения видимости элементов фигур. Для преобразования плоскости общего положения в плоскость уровня способом ЗПП требуется: Для преобразования плоскости общего положения в проецирующую плоскость способом ЗПП требуется: Для преобразования плоскости общего положения в проецирующую плоскость способом ППП требуется: Для преобразования плоскости общего положения в плоскость уровня способом ППП требуется: Для преобразования прямой общего положения в проецирующую прямую способом ЗПП требуется: Для преобразования прямой общего положения в проецирующую прямую способом ППП требуется: Для преобразования прямой общего положения в прямую уровня способом ППП требуется: Для преобразования прямой общего положения в прямую уровня способом ЗПП требуется: Тени, получаемые на неосвещенной поверхности фигуры, называются: Действительной тенью точки на плоскость проекций является: след светового луча на первой, встретившейся на его пути, плоскости проекций При стандартном освещении тень горизонтального отрезка на горизонтальной плоскости проекций: параллельна самому отрезку Преобразовать плоскость общего положения в горизонтальной плоскость уровня одним поворотом можно используя способ вращения вокруг горизонтали Для того что бы преобразовать общего положения в горизонтальную плоскость уровня одним поворотом ось вращения должна является Горизонтальная линия уровня По отношению к незаменяемой плоскости новая плоскость проекции располагается Расстояние от новой оси до новой проекции точки Равно расстоянию от заменяемой оси до заменяемой проекции точки Видео:Дифференциальная геометрия | параметризация простейших поверхностей | поверхности вращения | примерыСкачать  Уравнение окружности в параметрическом видеКардиоида Лемниската Бернулли Лемниската Бернулли – линия, представляющая геометрическое место точек, расстояние которых от двух данных точек (фокусов) есть постоянная величина, равная квадрату половины межфокусного расстояния. В полярных координатах Укажем, что точка М лежит на кривой, если выполнено условие Вершины кривой находятся в точках Площадь каждой петли S=a 2 . В полярных координатах Вершина кардиоиды находится в точке А(2а,0). Укажем, что площадь кардиоиды Видео:Дифференциальная геометрия | параметризации простейших кривых | окружностьСкачать 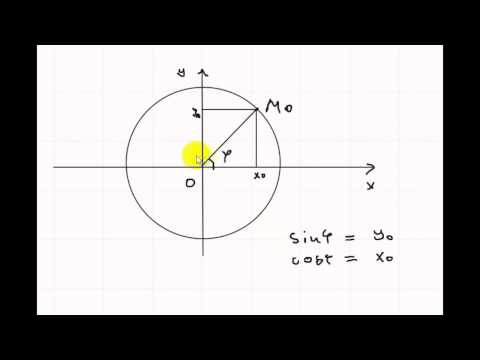 6. Параметрическое задание линийПараметрические уравнения линий задаются в виде зависимости текущих координат x и y от некоторого параметра t. Каждому значению t соответствуют два значения: x и y. При изменении параметра t текущая точка M(x,y) описывает некоторую кривую на плоскости.
Пусть M(x,y) – текущая точка окружности с центром в начале координат и радиусом R. В качестве параметра t выберем угол, который составляет радиус-вектор точки М с осью ox
Исключим из параметрических уравнений параметр t. Для этого возведём эти уравнения в квадрат и сложим их:
Дата добавления: 2013-12-13 ; Просмотров: 2896 ; Нарушение авторских прав? ; Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет Параметрическое представление — используемая в математическом анализе разновидность представления переменных, когда их зависимость выражается через дополнительную величину — параметр. Видео:Дифференциальная геометрия | плоская кривая и её параметризацияСкачать 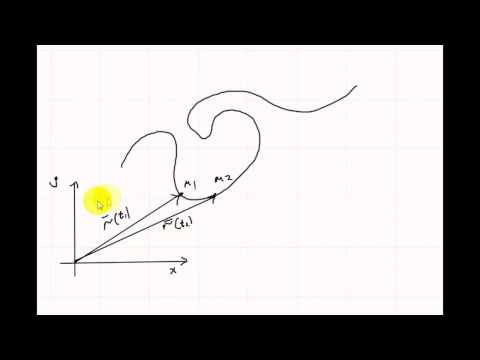 СодержаниеВидео:Дифференциальная геометрия | параметризации простейших кривых | циклоидаСкачать 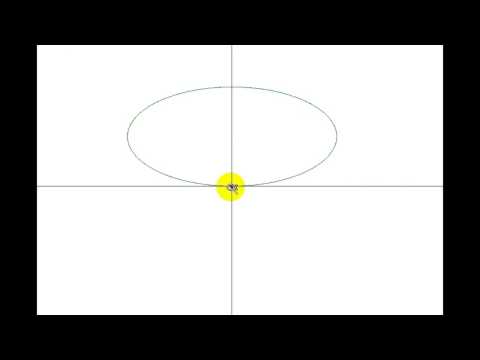 Параметрическое представление функции [ править | править код ]Предположим, что функциональная зависимость y от x не задана непосредственно y = f(x), а через промежуточную величину — t. Тогда формулы ;> задают параметрическое представление функции одной переменной. Если предположить, что обе эти функции φ и ψ имеют производные и для φ существует обратная функция θ, явное представление функции выражается через параметрическое как [1] : y = ψ ( θ ( x ) ) = f ( x ) и производная функции может быть вычислена как y ′ ( x ) = d y d x = y t ′ x t ′ = ψ ′ ( t ) ϕ ′ ( t ) >= >>= > Параметрическое представление даёт такое важное преимущество, что позволяет изучать неявные функции в тех случаях, когда их приведение к явному виду иначе как через параметры затруднительно. Видео:ТФКП. ИНТЕГРАЛ ПО ДУГЕ ОКРУЖНОСТИ от неаналитической функции. Метод замены переменной.Скачать  Параметрическое представление уравнения [ править | править код ]Параметрическое представление для более общего случая: когда переменные связаны уравнением (или системы уравнений, если переменных больше двух). Видео:Дифференциальная геометрия | параметризации простейших кривых | обобщённая винтовая линияСкачать  Параметрическое уравнение [ править | править код ]Близкое понятие — параметрическое уравнение [2] множества точек, когда координаты точек задаются как функции от некоторого набора свободных параметров. Если параметр один, мы получим параметрическое уравнение кривой. x = x ( t ) ; y = y ( t ) Выражая координаты точек поверхности через два свободных параметра, мы получим параметрическое задание поверхности. Примеры [ править | править код ]Уравнение окружности имеет вид: x 2 + y 2 = r 2 . +y^ =r^ .> Параметрическое уравнение окружности: ;> Параметрическое уравнение правой ветви гиперболы : t> Предположим, что функция $x=phi (t)$ имеет обратную функцию $t= (x)$. Тогда справедливо равенство: Параметрический способ задания функций широко применяется в механике. Так, если в плоскости некоторая материальная точка находится в движении (время $t$), и законы движения проекций этой точки на оси координат известны: Уравнения являются параметрическими уравнениями траекторий движущейся точки. Исключая временной параметр, получим уравнение траектории в форме $y = f(x)$. Определить траекторию и место падения груза, сброшенного с самолета, движущегося горизонтально со скорость $v_0$ на высоте $y_0$. Допустим, что груз сбрасывается с момент пересечения самолетом оси Oy. Тогда очевидно, что горизонтальное перемещение груза равномерно и имеет постоянную скорость: А вертикальное перемещение: Следовательно, расстояние от груза до земли в произвольный момент падения: Уравнения горизонтального и вертикального перемещения тела являются параметрическими. Для того, чтобы исключить временной параметр $t$, найдем его значение из первого уравнения. Полученное выражение подставим во второе параметрическое уравнение чтобы найти уравнение траектории: Попробуй обратиться за помощью к преподавателям Видео:Дифференциальная геометрия | параметризации простейших кривых | винтовая линияСкачать  Уравнения некоторых кривых в параметрической форме:
Параметрические кривые окружности: Рисунок 1. Окружность и ее параметрические кривые Уравнение гиперболы имеет вид: Параметрические кривые гиперболы: Рисунок 2. Гипербола и ее параметрические кривые Записать уравнение окружности в параметрическом виде.
Значит, радиус $r$ равен 6. Задай вопрос специалистам и получи Записать уравнение гиперболы в параметрическом виде. Так и не нашли ответ Просто напиши с чем тебе 🌟 ВидеоУравнение окружности (1)Скачать  ТФКП. Вычислить интеграл от функции комплексного переменного по данной кривой. Дуга окружности.Скачать  Дифференциальная геометрия | параметризации простейших кривых | обобщённая винтовая линия | примерСкачать  ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать  ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать  Параметризация в AutoCAD 2015 - создание сложных блоковСкачать  Пенской А.В. - Классическая дифференциальная геометрия.Лекции - 1. ВведениеСкачать  1 2 4 сопряжение окружностейСкачать  Параметр. Серия 14. Решение задач с окружностями. Касание окружности и гиперболыСкачать  Шафаревич А.И.- Дифференциальная геометрия - 1. Геометрия кривых. Плоские кривыеСкачать  Пенской А. В. - Аналитическая геометрия - Коники в проективной геометрииСкачать  |








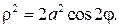
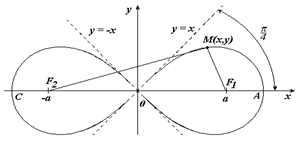
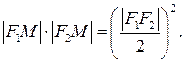
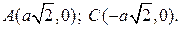
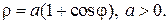
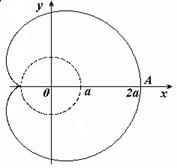
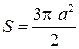 , а длина L=8a.
, а длина L=8a.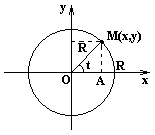
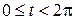 . Из треугольника ОМА:
. Из треугольника ОМА: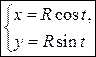 – параметрические уравнения окружности.
– параметрические уравнения окружности.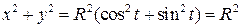 .
.
 y = ψ ( t )
y = ψ ( t )