Параллелограмм ABCD и треугольник DAM размещены так, что точка Мне принадлежит плоскости ABC. Точка О — точка пересечения диагоналей ABCD. Найдите линию скрещения плоскостей: а) ВМС и OMD- б) BMD и АСМ.
Помогите!!
- Тоха Кладинов
- Геометрия 2019-08-22 21:53:54 0 1
3. Плоскости ADK и ОСК пересекаются по прямой АК;
Плоскости BDK и АС К. пересекаются по прямой ОК
Видео:№42. Даны параллелограмм ABCD и трапеция ABEK с основанием ЕК, не лежащие в одной плоскости,Скачать
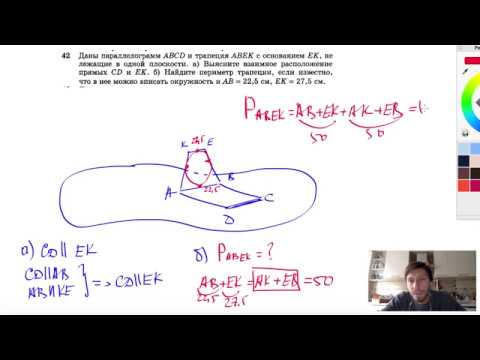
Задача 56357 Параллелограмм АБСД и треугольник АМВ.
Условие
Параллелограмм АБСД и треугольник АМВ пересекаются по прямой АБ. Определите как расположено: А) Средняя линия ЕФ треугольника АБС и прямая СД Б) Прямая ЕФ и плоскость АДС .
Решение
EF|| AB — так как EF — средняя линия Δ AMB
AB|| CD — по свойству сторон параллелограмма
( две прямые параллельные третьей параллельны между собой)
б) EF || СD ⇒ || АВСD
См скрин ( признак параллельности прямой и плоскости)
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Параллелограмм
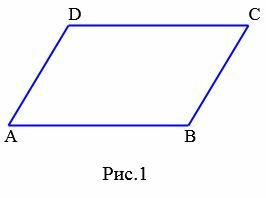
Определение 1. Параллелограммом называется четырехугольник, у которого противоположные стороны параллельны.
На Рис.1 изображен параллелограмм поскольку ( small AB || CD, ;; AD || BC .)
 |
Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Свойства параллелограмма
Свойство 1. В параллелограмме противоположные углы равны и противоположные стороны равны.
Доказательство. Рассмотрим параллелограмм ABCD (Рис.2).
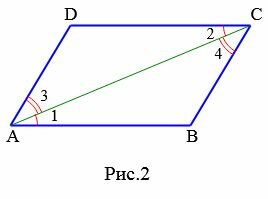 |
Диагональ AC разделяют параллелограмм на два треугольника ACB и ACD. ( small angle 1=angle 2 ) поскольку эти углы накрест лежащие, при рассмотрении параллельных прямых AB и CD пересеченные секущей AC (см. теорему 1 статьи Теоремы об углах, образованных двумя параллельными прямыми и секущей). Аналогично ( small angle 3=angle 4 ), если рассмотреть параллельные прямые AD и BC пересеченные секущей AC. Тогда треугольники ACB и ACD равны по одной стороне и двум прилежащим углам: AC общая, ( small angle 1=angle 2 ), ( small angle 3=angle 4 ) (см. статью Треугольники. Признаки равенства треугольников). Поэтому ( small AB=CD, ;; AD=BC, ;; angle B=angle D. )
Из рисунка Рис.2 имеем: ( small angle A=angle 1+angle 3, ;; angle C=angle 2+angle 4. ) Учитывая, что ( small angle 1=angle 2 ) и ( small angle 3=angle 4 ), получим: ( small angle A=angle C. )
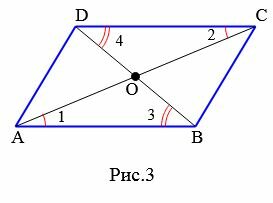
Свойство 2. Диагонали параллелограмма точкой пересечения разделяются пополам.
Доказательство. Рассмотрим параллелограмм ABCD (Рис.3) и пусть O точка пересечения диагоналей AC и BD. ( small angle 1=angle 2 ) поскольку эти углы накрест лежащие, при рассмотрении параллельных прямых AB и CD пересеченные секущей AC. ( small angle 3=angle 4 ), если рассмотреть параллельные прямые AB и CD пересеченные секущей BD. Поскольку в параллелограмме противоположные стороны равны: AB=CD (Свойство 1), то треугольники ABO и CDO равны по стороне и прилежашим двум углам. Тогда AO=OC и BO=OD.
 |
Видео:Биссектриса параллелограммаСкачать

Признаки параллелограмма
Признак 1. Если в четырехугольнике две стороны параллельны и равны, то этот четырехугольник является параллелограммом.
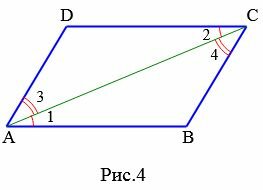 |
Доказательство. Рассмотрим параллелограмм ABCD. Пусть AB=CD и AB || CD. Проведем диагональ AC (Рис.4). Поскольку AB || CD, то ( small angle 1=angle 2 ) как накрест лежащие углы − при рассмотрении параллельных прямых AB и CD пересеченных секущей AC. Тогда треугольники ACB и ACD равны, по двум сторонам и углу между ними. Действительно, AB=CD, AC− общая сторона ( small angle 1=angle 2 ). Но тогда ( small angle 3=angle 4. ) Рассмотрим прямые AD и BC, пересеченные секущей AC. Поскольку ( small angle 3 ) и ( small angle 4 ) являются накрест лежашими углами, то по теореме 1 статьи Параллельные прямые. Признаки параллельности прямых, эти прямые параллельны. Таким образом, в четырехугольнике противоположные стороны попарно параллельны (AB || CD, AD || BC) и, значит, данный четырехугольник параллелограмм.
Признак 2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник является параллелограммом.
Доказательство. Рассмотрим параллелограмм ABCD (Рис.4). Проведем диагональ AC (Рис.4). Рассмотрим треугольники ACB и ACD. Эти треугольники равны по трем сторонам (см. статью Треугольники. Признаки равенства треугольников). Действительно. AC − общая для этих треугольников и по условию AB = CD, AD = BC. Тогда ( small angle 1=angle 2 ). Отсюда следует AB || CD. Имеем, AB = CD, AB || CD и по признаку 1 четырехугольник ABCD является параллелограммом.
Признак 3. Если в четырехугольнике диагонали пересекаются и точкой пересечения разделяются пополам, то данный четырехугольник − параллелограмм.
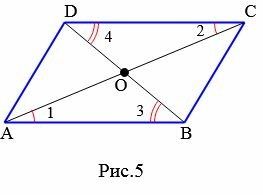 |
Доказательство. Рассмотрим четырехугольник ABCD (Рис.5). Пусть диагонали четырехугольника пересекаются в точке O и точкой пересечения делятся пополам:
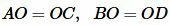 |
Углы AOB и COD вертикальные, следовательно ( small angle AOB=angle COD ). Тогда треугольники AOB и COD равны по двум сторонам и углу меду ними:
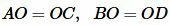 , , 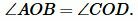 |
Тогда AB = CD и ( small angle 1=angle 2 ). Но по признаку параллельности прямых следует, что AB || CD (теорема 1 статьи Параллельные прямые. Признаки параллельности прямых). Получили:
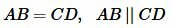 |
и, по признаку 1 четырехугольник ABCD − параллелограмм.
🎬 Видео
№933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать

Геометрия 8 класс. Параллелограмм, свойства параллелограммаСкачать

№447. Начертите параллелограмм ABCD и отметьте точку М, симметричную точке D относительноСкачать

№45. Прямая а параллельна стороне ВС параллелограмма ABCD и не лежит в плоскости параллелограмма.Скачать

Высота, биссектриса, медиана. 7 класс.Скачать

Задача №24. ОГЭ по математике. | Математика | TutorOnlineСкачать

8 класс, 4 урок, ПараллелограммСкачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

ОГЭ за одну минуту. Математика, задание 17 (параллелограмм).Скачать

Интересный гидравлический домкрат. Сибталь LJ.Скачать

№770. Дан параллелограмм ABCD. Выразите вектор АС через векторы а и b , если:Скачать

Параллелограмм. Практическая часть - решение задачи. 8 класс.Скачать

Диагональ AC параллелограмма ABCD образует ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

№374. Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке КСкачать



