— подготовка к контрольной работе.
Дано: ABCD — параллелограмм, АА1 и СС1. Прямые АА1 и СС1 не лежат в одной плоскости параллелограмма (рис. 1).
Доказать: (А1АВ) || (C1CD).
Решение: АВ || CD — противоположные стороны параллелограмма, АА1 || СС1 по условию. BA ∩ AA1 = A, DC ∩ СС1 = С. По признаку параллельности плоскостей (А1АВ) || (C1CD). Что и требовалось доказать.
Дано: 

а) Доказать: А1В1 || А2В2.
а) Из определения параллельных прямых в пространстве следует, что прямые а и b лежат в одной плоскости, которая пересекает параллельные плоскости α и β по прямым А1В1 и А2В2. По 1° свойству параллельных плоскостей А1В1 || А2В2. Что и требовалось доказать.
б) Отрезки А1А2 || В1В2, так как α || β по условию. А1В1 || А2В2 по выше доказанному. Значит, А2В2В1А1 — параллелограмм по определению. По свойству параллелограмма (сумма углов, прилежащих к одной стороне, равна 180°) 

Дано: ABCD — параллелограмм. Прямые АА1 и СС1 не лежат в плоскости параллелограмма АА1 || СС1 (рис. 3).
Доказать: (A1AD) || (С1СВ).
Решение: ВС || AD — противоположные стороны параллелограмма. СС1 || АА1 по условию; 
Дано: 

а) Доказать: А1В1 = А2В2.
а) Отрезки А1А2 и B1В2 параллельных прямых а и b параллельны, то есть А1А2 || B1B2. а || Р, α || β по условию. Следовательно, по свойству 2° параллельных плоскостей А1А2 = В1В2. Значит, противоположные стороны А1А2 и В1В2 четырехугольника А2В2В1А1 равны и параллельны и А2В2В1А1 — параллелограмм. В параллелограмме противолежащие стороны равны, поэтому А1В1 = A2В2, что и требовалось доказать.
б) В параллелограмме противоположные углы равны, ∠B1A1A2 = ∠B1B2A2, так как ∠B1A1A2 = 50°, то ∠B1B2A2 = 50°. (Ответ: ∠B1B2A2 = 50°.)
Дано: ABCD и A1B1CD параллелограммы не лежат в одной плоскости (рис. 5).
Доказать: (ADA1) || (ВСВ1).

Дано: 
Доказать: a) АВ || CD; б) ∠ADC четырехугольника ABCD равен 65°.
Найти остальные углы.
Решение: Прямые АС и BD пересекаются и задают плоскость ABCD. По свойству параллельных плоскостей (п. 11, 1°) АВ || CD, ΔAОВ = ΔDOC по второму признаку 
Из равенства треугольников следует, что OB = OD, АО = СО, то есть диагонали четырехугольника делятся точкой пересечения пополам. Значит, ABCD — параллелограмм. У параллелограмма противоположные углы равны. Если ∠ADC = 65 °, то ∠ABC = 65 °, ∠DAB = 180° — ∠ADC = 180° — 65° = 115°. ∠BCD = ∠DAB = 115°. (Ответ: 65°, 115°, 115°.)
Дано: ABCD и ABC1D1 — параллелограммы не лежат в одной плоскости (рис. 7).
Доказать: (СВС1) || (DAD1).
Решение: 


Дето: 
а) Доказать: AD || ВС.
б) Найти: ∠ABC, ∠ADC, ∠BCD.
а) Две пересекающиеся прямые единственным образом задают плоскость. Отрезки АС и BD пересекаются и задают плоскость ABCD, которая пересекает параллельные плоскости аир по прямым АВ и DC. По свойству 1° параллельных плоскостей АВ || DC. АВ = DC по условию.
Поэтому четырехугольник ABCD — параллелограмм. Значит, AD || ВС. Что и требовалось доказать.
б) В параллелограмме сумма углов, прилежащих к одной стороне равна 180°. 
Дано: 
При каком взаимном расположении прямых а и b α || β?
Решение: α || β, если прямые а и b пересекаются.
Две пересекающиеся прямые единственным образом задают плоскость. Прямые а и b пересекаются и задают плоскость γ. Пересекающиеся прямые а и b плоскости γ параллельны плоскости α. Значит, α || γ (задача 51). Рассуждая аналогично, имеем β || γ, α || γ, α || у. Следовательно, α || β (задача 60).
Дано: α || β. Отрезки АС и BD пересекаются в точке О, 
а) При каком дополнительном условии пересечения отрезков ABCD — прямоугольник?
б) Доказать: ABCD — равнобокая трапеция.
а) Две пересекающиеся прямые единственным образом задают плоскость.
Отрезки АС и BD пересекаются и задают плоскость ABCD. По 1° свойству параллельных плоскостей АВ || CD. По условию АС = BD. При дополнительном условии, что пересекающиеся отрезки делятся точкой пересечения пополам, ABCD будет являться прямоугольником.
б) Из выше доказанного АВ || CD. Значит, ABCD — трапеция по определению. AC || BD — ее диагонали. Если диагонали трапеции равны, то она равнобедренная. АС = BD по условию.
Значит, ABCD — равнобокая трапеция.
Дано: 
При каком взаимном расположении прямых а и b α || β?
Решение: 



Дано: 

а) При каком дополнительном условии пересечения отрезков ABCD — квадрат?
б) Доказать, что ABCD трапеция, в которой высота равна средней линии.
а) По свойству 1° параллельных АВ || DC. При условии, что отрезки точкой пересечения делятся пополам, ABCD будет являться квадратом.
б) ΔBDC = ΔADC (по двум сторонам и угу между ними. DC — общая, AD = BC, ∠ADC = ∠BCD как углы при основании равнобедренной трапеции).
Из равенства треугольников следует, что ∠BDC = ∠ACD. Тогда DO = ОС. ΔDOC — прямоугольный и равнобедренный. ОМ — высота,, биссектриса, медиана. ΔОМС — прямоугольный равнобедренный. ОМ = МС или ОМ = 1/2DC.
Аналогично 

Примечание: Задачи решаются учащимися самостоятельно. Уровень выбирают ученики. Анализ решений делает учитель.
Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.
Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.
Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.
Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.
© 2014-2021 Все права на дизайн сайта принадлежат С.Є.А.
Видео:Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

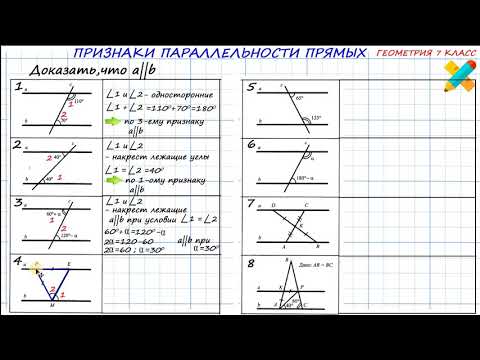
Параллельные прямые доказать ab параллельно cd
305. Параллельны ли изображённые на рисунке 212 прямые a и b , если:
3) ∠ 4 = 125°, ∠ 6 = 55°;
4) ∠ 2 = 35°, ∠ 5 = 146°;
5) ∠ 1 = 98°, ∠ 6 = 82°;
6) ∠ 1 = 143°, ∠ 7 = 37°?
306. На каких из рисунков 213, а – г прямые m и n параллельны?
307. На рисунке 214 укажите все пары параллельных прямых.
308. На рисунке 215 укажите параллельные прямые, если ∠ 1 = 53°, ∠ 2 = 128°, ∠ 3 = 127°.
309. На рисунке 216 AB = BC , CD = DK . Докажите, что AB ‖ DK .
310. На рисунке 217 AK — биссектриса угла BAC , AM = MK . Докажите, что MK ‖ AC .
311. На рисунке 218 ∠ ACB = ∠ ACD , AD = CD . Докажите, что BC ‖ AD .
312. В треугольнике ABC известно, что AB = BC , ∠ A = 60°, ∠ BCD — смежный с ∠ ACB , CM — биссектриса угла BCD . Докажите, что AB ‖ CM .
313. Отрезки AB и CD пересекаются в точке O и делятся этой точкой пополам. Докажите, что AC ‖ BD .
314. На рисунке 219 AB = CD , BC = AD . Докажите, что AB ‖ CD .
315. Известно, что некоторая прямая m пересекает прямую a (рис. 220). Пересекает ли прямая m прямую b ?
316. Каково взаимное расположение прямых CD и EF на рисунке 221?
317. Угол ABC равен 60°, а угол BCD — 120°. Можно ли утверждать, что прямые AB и CD параллельны?
318. Угол между прямыми a и c равен углу между прямыми b и c . Можно ли утверждать, что прямые a и b параллельны?
319. Четыре угла, образованные при пересечении прямых a и b прямой c , равны по 40°, а любой из остальных четырёх углов — 140°. Можно ли утверждать, что прямые a и b параллельны?
320. Прямая пересекает биссектрису BM треугольника ABC в точке O , являющейся серединой отрезка BM , а сторону BC — в точке K . Докажите, что если OK ⊥ BM , то MK ‖ AB .
321. Отрезки AM и CK — медианы треугольника ABC . На продолжении отрезка AM за точку M отложен отрезок MF , а на продолжении отрезка CK за точку K — отрезок KD так, что MF = AM , KD = CK . Докажите, что точки B , D и F лежат на одной прямой.
Упражнения для повторения
322. Луч OC разбивает угол AOB на два угла так, что ∠ AOC : ∠ BOC = 3 : 5. Найдите угол между лучом OC и биссектрисой угла, смежного с углом AOB , если угол BOC на 42° больше угла AOC .
323. На рисунке 222 AB = BC , ∠ ABK = ∠ CBM . Докажите, что BM = BK .
324. Равнобедренные треугольники ABC и ADC имеют общее основание AC . Прямая BD пересекает отрезок AC в точке E . Докажите, что AE = EC .
Наблюдайте, рисуйте, конструируйте, фантазируйте
325. Приведите пример, когда общей частью (пересечением) треугольника и четырёхугольника является восьмиугольник.
Когда сделаны уроки
Пятый постулат Евклида
В § 6 вы узнали, что в качестве аксиом выбирают очевидные утверждения. Тогда почему бы, например, теоремы 1.1 и 5.1 не включить в список аксиом, ведь они тоже очевидны? Ответ на этот вопрос понятен: если какое-то утверждение можно доказать с помощью аксиом, то это утверждение — теорема, а не аксиома. С этих позиций очень поучительна история, связанная с пятым постулатом Евклида
V постулат. И чтобы всякий раз, когда прямая при пересечении с двумя другими прямыми образует с ними односторонние углы, сумма которых меньше двух прямых, эти прямые пересекались с той стороны от секущей, с которой эта сумма меньше двух прямых углов ( рис. 223 ).
Можно показать, что пятый постулат и сформулированная нами в § 13 аксиома параллельности прямых равносильны, т. е. из постулата следует аксиома и наоборот — из аксиомы следует постулат.
Более двадцати веков многие учёные пытались доказать пятый постулат, т. е. вывести его из других аксиом Евклида. Лишь в начале XIX в. несколько математиков независимо друг от друга пришли к выводу: утверждение, что через данную точку, не лежащую на данной прямой, мож но провести только одну прямую, параллельную данной , является аксиомой.
Вам может показаться, что в этом выводе ничего особенного нет: присоединяем аксиому параллельности к уже существующему списку аксиом-правил, а дальше доказываем теоремы.
Однако если в футболе добавить только одно правило, например разрешить полевым игрокам играть и руками, то мы получим совершенно новую игру.
Если пятый постулат — это правило, которое мы принимаем, а не теорема, то его можно заменить противоположным утверждением.
Так и поступил Н.И. Лобачевский. Он заменил лишь одно правило — аксиому параллельности прямых — следующим: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, не пересекающие данную. Новая аксиома позволила построить новую геометрию — неевклидову.
Н.И. Лобачевский (1792–1856)
Выдающийся русский математик, про-
фессор Казанского университета.
С подобной идеей несколько позже выступил венгерский математик Янош Бойяи (1802–1860).
Видео:7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

Параллельные прямые доказать ab параллельно cd
Противолежащие стороны параллелограмм равны.
Доказательство.
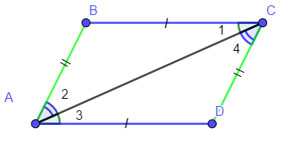
На рисунке изображён параллелограмм ABCD. Докажем, что АВ = CD и ВС = AD .
Проведём диагональ АС. Рассмотрим треугольники ABC и ACD .
В этих треугольниках сторона AC общая, углы 1 и ∠3 равны как накрест лежащие при параллельных прямых ВС и AD и секущей AC,
углы ∠ 2 и ∠4 равны как накрест лежащие при параллельных прямых AB и CD и секущей AC.
Следовательно, треугольники ABC и ADC равны по второму признаку равенства треугольников. Отсюда АВ = CD и ВС = AD .
Докажите теорему:
Противолежащие стороны параллелограмм равны.
Доказательство.
На рисунке изображён параллелограмм ABCD. Докажем, что АВ = _______ и ВС = _____.
Проведём диагональ АС. Рассмотрим треугольники ABC и _______ .
В этих треугольниках сторона ______ общая, углы 1 и ____ равны как __________________________ при _________________ прямых ____ и _____ и секущей ____, углы ____ и _____ равны как ____________________________ при ____________________ прямых ___________ и секущей _____.
Следовательно, треугольники ______ и ________ равны по _______________ признаку равенства треугольников. Отсюда АВ = ________ и ВС = _____.
🎥 Видео
Параллельные прямые | Математика | TutorOnlineСкачать

Параллельные прямые (задачи).Скачать

10 класс, 5 урок, Параллельность трех прямыхСкачать

10 класс, 4 урок, Параллельные прямые в пространствеСкачать

Параллельность прямых. 10 класс.Скачать

Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

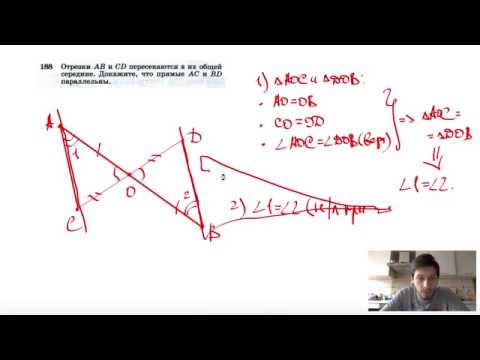
№188. Отрезки АВ и CD пересекаются в их общей середине. Докажите, что прямые АССкачать
7 класс, 28 урок, Аксиома параллельных прямыхСкачать

Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Параллельные прямые — Признак Параллельности Прямых и Свойства УгловСкачать

10 класс, 7 урок, Скрещивающиеся прямыеСкачать

7 класс, 24 урок, Определение параллельных прямыхСкачать

Геометрия 7 класс (Урок№21 - Свойства параллельных прямых.)Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. §13 геометрия 7 классСкачать

10 класс - Геометрия - Параллельные прямые в пространстве. Параллельность трёх прямыхСкачать

7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

Задачи. Признак параллельности прямых. Доказать, что прямые параллельны. По рисунку.Скачать