В задачах на построение сечений мы применяем все те определения, теоремы, свойства и признаки, которые изучаем и доказываем на уроках в школе.
Например, если две плоскости имеют общую точку, то они пересекаются по прямой. Это значит, что плоскость сечения и, например, плоскость грани пирамиды будут пересекаться по прямой, и на чертеже будет показана часть этой прямой – отрезок.
Как вы думаете — может ли восьмиугольник быть сечением куба?
И может ли правильный пятиугольник быть сечением куба?
Чтобы соединить какие-либо две точки на чертеже, нам нужна плоскость, в которой эти точки лежат. Иногда это грань объемного тела. Иногда – вспомогательная плоскость.
А вообще сечение — это плоская фигура, которая образуется при пересечении объемного тела плоскостью и граница которой лежит на поверхности этого объемного тела.
Конечно, восьмиугольник сечением куба быть не может. Ведь у куба 6 граней, и поэтому сечение куба не может иметь больше 6 сторон.
При построении сечений мы часто используем следующие теоремы:
1. Линии пересечения параллельных плоскостей третьей плоскостью параллельны.
Именно поэтому правильный пятиугольник не может быть сечением куба. Ведь 4 из 5 сторон этого пятиугольника лежат в параллельных гранях куба и поэтому параллельны. А у правильного пятиугольника параллельных сторон нет.
2. Теорема о прямой и параллельной ей плоскости:
Пусть прямая m параллельна плоскости α. Если плоскость β проходит через прямую m и пересекает плоскость α по прямой c, то c параллельна m.
Эта теорема помогает, например, при построении сечений пирамиды.
Разберем несколько задач на построение сечений.
1. Постройте сечение тетраэдра плоскостью, проходящей через точки М, N, K. Точка М лежит на ребре AD, N — на ребре DC, К — на ребре АВ.
Проведем МК в плоскости грани ABD и MN в плоскости грани ADC.
Продлим отрезки MN и АС;
Проведем РК в плоскости нижней грани; четырехугольник — искомое сечение.
2. Постройте сечение тетраэдра плоскостью, проходящей через точки М, N, K. Точка N лежит на ребре
Покажем, что плоскость сечения пересекает плоскость основания пирамиды по прямой NT, параллельной МК.
Прямая МК параллельна АВ, лежащей в плоскости основания АВС. Значит,
Плоскость сечения проходит прямую МК, параллельную плоскости АВС. По теореме о прямой и параллельной ей плоскости, линия пересечения плоскости сечения и плоскости АВС параллельна прямой МК. Трапеция MKNT — искомое сечение.
3. Постройте сечение куба проходящее через вершину и середины ребер и
Пусть М — середина АВ, N — середина ВС, Продолжим прямую MN до пересечения с продолжениями ребер DC и AD;
Треугольники АМР и KCN — прямоугольные равнобедренные, причем
Проведем — в плоскости задней грани и — в плоскости левой грани куба;
Пятиугольник — искомое сечение. В нем есть параллельные стороны: так как линии пересечения параллельных плоскостей третьей плоскостью параллельны.
4. Постройте сечение куба проходящее через вершину В и середины ребер и
Пусть М — середина ребра , N — середина ребра
Поскольку линии пересечения параллельных плоскостей третьей плоскостью параллельны, плоскость сечения пересекает заднюю грань по прямой, параллельной ВМ, а левую грань — по прямой, параллельной BN. Тогда искомое сечение — ромб
5. Постройте сечение правильного тетраэдра АВСS, проходящее через точку К — середину ребра АВ, точку М, делящую ребро АS в отношении , и точку N — середину апофемы грани SBC.
Пусть SH — апофема грани SBC; N—середина SH.
Проведем MN в плоскости ASH;
Четырехугольник KMEF — искомое сечение.
Постройте сечение правильного тетраэдра АВСS, проходящее через точку К — середину ребра АВ, и точки М и Т — центры граней АSС и SBC.
Пусть SЕ и SH — апофемы граней ASC и SBC; точки М и Т делят отрезки SЕ и SH в отношении 2:1, считая от точки S.
Из подобия треугольников SMT и SEH получим, что Значит
По теореме о прямой и параллельной ей плоскости, линия пересечения плоскости сечения и нижней грани параллельна прямой МТ. Это значит, что плоскость сечения пересекает грань АВС по прямой АВ. Достроим сечение.
7. Постройте сечение куба , проходящее через точку М, лежащую на ребре и точки Т и К, принадлежащие граням АВС и .
Точки М и К лежат в плоскости задней грани . Соединив М и К, получим, что
Соединив точки Р и Т в нижней грани, получим FN — линию пересечения плоскости сечения с нижней гранью;
. Трапеция FMEN — искомое сечение.
8. И самый сложный случай. Построим сечение куба плоскостью МNK, где , причем расстояния от точек М и N до плоскости АВС различны.
Пусть точки и — проекции точек M и N на плоскость нижней грани
Плоскость проходит через параллельные прямые и .
Проведем в этой плоскости MN и
Точки Р и К лежат в нижней грани куба, следовательно, плоскость сечения пересекает нижнюю грань по прямой РК. Дальнейшее построение — очевидно.
Видео:10 класс, 14 урок, Задачи на построение сеченийСкачать

Параллельное сечение в треугольнике
Правила построения сечений многогранников:
1) проводим прямые через точки, лежащие в одной плоскости;
2) ищем прямые пересечения плоскости сечения с гранями многогранника, для этого
а) ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости);
б) параллельные грани плоскость сечения пересекает по параллельным прямым.
Примеры построения сечений:
Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1. Построим сечение, проходящее через точки M, N, L.
Соединим точки M и L, лежащие в плоскости AA1D1D.
Пересечем прямую ML ( принадлежащую сечению) с ребром A1D1, они лежат в одной плоскости AA1D1D. Получим точку X1.
Точка X1 лежит на ребре A1D1, а значит и плоскости A1B1C1D1, соединим ее сточкой N, лежащей в этой же плоскости.
X1 N пересекается с ребром A1B1 в точке К.
Соединим точки K и M, лежащие в одной плоскости AA1B1B.
Найдем прямую пересечения плоскости сечения с плоскостью DD1C1C:
пересечем прямую ML (принадлежащую сечению) с ребром DD1, они лежат в одной плоскости AA1D1D, получим точку X2;
пересечем прямую KN (принадлежащую сечению) с ребром D1C1, они лежат в одной плоскости A1B1C1D1, получим точку X3;
Точки X2 и X3 лежат в плоскости DD1C1C. Проведем прямую X2 X3 , которая пересечет ребро C1C в точке T, а ребро DC в точке P. И соединим точки L и P, лежащие в плоскости ABCD.
MKNTPL — искомое сечение.
Рассмотрим ту же самую задачу на построение сечения, но воспользуемся свойством параллельных плоскостей. Это облегчит нам построение сечения.

Соединим точки M и L, лежащие в плоскости AA1D1D.

Через точку N, проведем прямую NT параллельную прямой ML. Прямые NT и ML лежат в параллельных плоскостях по свойству параллелепипеда.

Пересечем прямую ML ( принадлежащую сечению) с ребром A1D1, они лежат в одной плоскости AA1D1D. Получим точку X1.

Точка X1 лежит на ребре A1D1, а значит и плоскости A1B1C1D1, соединим ее сточкой N, лежащей в этой же плоскости.
X1 N пересекается с ребром A1B1 в точке К.

Соединим точки K и M, лежащие в одной плоскости AA1B1B.

Проведем прямую TP через точку T, параллельно прямой KM ( они лежат в параллельных плоскостях).

Соединим точки P и L ( они лежат в одной плоскости).

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Построение сечений
Определение
Сечение — это плоская фигура, которая образуется при пересечении пространственной фигуры плоскостью и граница которой лежит на поверхности пространственной фигуры.
Замечание
Для построения сечений различных пространственных фигур необходимо помнить основные определения и теоремы о параллельности и перпендикулярности прямых и плоскостей, а также свойства пространственных фигур. Напомним основные факты.
Для более подробного изучения рекомендуется ознакомиться с темами “Введение в стереометрию. Параллельность” и “Перпендикулярность. Углы и расстояния в пространстве”.
Важные определения
1. Две прямые в пространстве параллельны, если они лежат в одной плоскости и не пересекаются.
2. Две прямые в пространстве скрещиваются, если через них нельзя провести плоскость.
3. Прямая и плоскость параллельны, если они не имеют общих точек.
4. Две плоскости параллельны, если они не имеют общих точек.
5. Две прямые в пространстве называются перпендикулярными, если угол между ними равен (90^circ) .
6. Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
7. Две плоскости называются перпендикулярными, если угол между ними равен (90^circ) .
Важные аксиомы
1. Через три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
2. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
3. Через две пересекающиеся прямые проходит плоскость, и притом только одна.
Важные теоремы
1. Если прямая (a) , не лежащая в плоскости (pi) , параллельна некоторой прямой (p) , лежащей в плоскости (pi) , то она параллельна данной плоскости.
2. Пусть прямая (p) параллельна плоскости (mu) . Если плоскость (pi) проходит через прямую (p) и пересекает плоскость (mu) , то линия пересечения плоскостей (pi) и (mu) — прямая (m) — параллельна прямой (p) .
3. Если две пересекающиеся прямых из одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости будут параллельны.
4. Если две параллельные плоскости (alpha) и (beta) пересечены третьей плоскостью (gamma) , то линии пересечения плоскостей также параллельны:
[alphaparallel beta, alphacap gamma=a, betacapgamma=b Longrightarrow aparallel b]
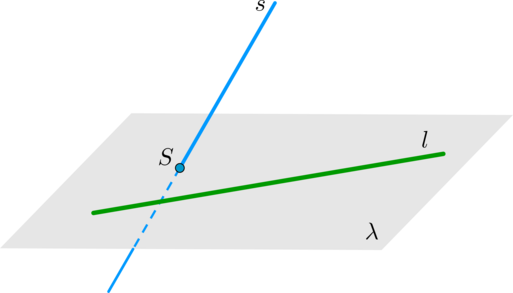
5. Пусть прямая (l) лежит в плоскости (lambda) . Если прямая (s) пересекает плоскость (lambda) в точке (S) , не лежащей на прямой (l) , то прямые (l) и (s) скрещиваются.
6. Если прямая перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости, то она перпендикулярна этой плоскости.
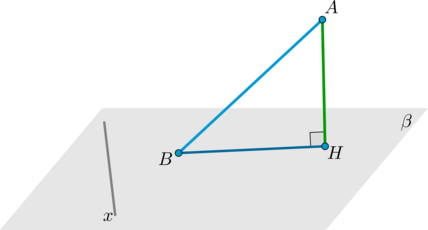
7. Теорема о трех перпендикулярах.
Пусть (AH) – перпендикуляр к плоскости (beta) . Пусть (AB, BH) – наклонная и ее проекция на плоскость (beta) . Тогда прямая (x) в плоскости (beta) будет перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции.
8. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то она перпендикулярна этой плоскости.
Замечание
Еще один важный факт, часто использующийся для построения сечений:
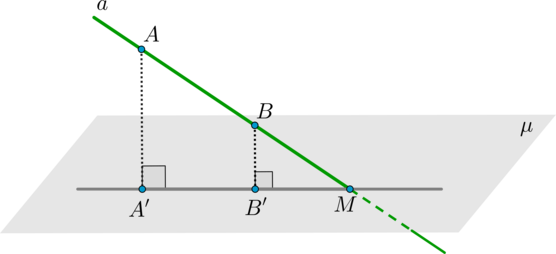
для того, чтобы найти точку пересечения прямой и плоскости, достаточно найти точку пересечения данной прямой и ее проекции на эту плоскость.
Для этого из двух произвольных точек (A) и (B) прямой (a) проведем перпендикуляры на плоскость (mu) – (AA’) и (BB’) (точки (A’, B’) называются проекциями точек (A,B) на плоскость). Тогда прямая (A’B’) – проекция прямой (a) на плоскость (mu) . Точка (M=acap A’B’) и есть точка пересечения прямой (a) и плоскости (mu) .
Причем заметим, что все точки (A, B, A’, B’, M) лежат в одной плоскости.
Пример 1.
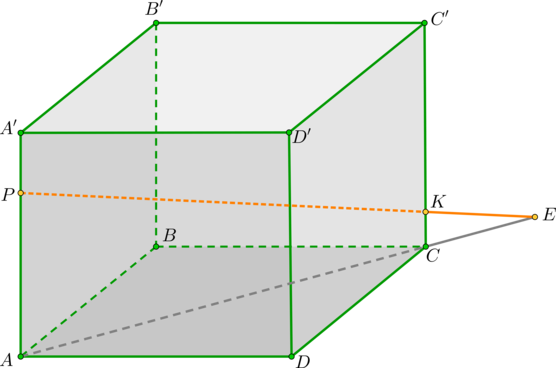
Дан куб (ABCDA’B’C’D’) . (A’P=dfrac 14AA’, KC=dfrac15 CC’) . Найдите точку пересечения прямой (PK) и плоскости (ABC) .
Решение
1) Т.к. ребра куба (AA’, CC’) перпендикулярны ((ABC)) , то точки (A) и (C) — проекции точек (P) и (K) . Тогда прямая (AC) – проекция прямой (PK) на плоскость (ABC) . Продлим отрезки (PK) и (AC) за точки (K) и (C) соответственно и получим точку пересечения прямых – точку (E) .
2) Найдем отношение (AC:EC) . (triangle PAEsim triangle KCE) по двум углам ( (angle A=angle C=90^circ, angle E) – общий), значит, [dfrac=dfrac]
Если обозначить ребро куба за (a) , то (PA=dfrac34a, KC=dfrac15a, AC=asqrt2) . Тогда:
Пример 2.
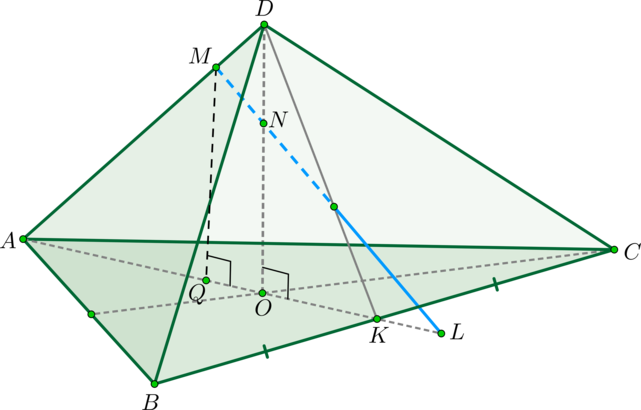
Дана правильная треугольная пирамида (DABC) с основанием (ABC) , высота которой равна стороне основания. Пусть точка (M) делит боковое ребро пирамиды в отношении (1:4) , считая от вершины пирамиды, а (N) – высоту пирамиды в отношении (1:2) , считая от вершины пирамиды. Найдите точку пересечения прямой (MN) с плоскостью (ABC) .
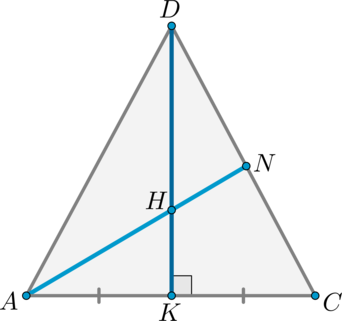
Решение
1) Пусть (DM:MA=1:4, DN:NO=1:2) (см. рисунок). Т.к. пирамида правильная, то высота падает в точку (O) пересечения медиан основания. Найдем проекцию прямой (MN) на плоскость (ABC) . Т.к. (DOperp (ABC)) , то и (NOperp (ABC)) . Значит, (O) – точка, принадлежащая этой проекции. Найдем вторую точку. Опустим перпендикуляр (MQ) из точки (M) на плоскость (ABC) . Точка (Q) будет лежать на медиане (AK) .
Действительно, т.к. (MQ) и (NO) перпендикулярны ((ABC)) , то они параллельны (значит, лежат в одной плоскости). Следовательно, т.к. точки (M, N, O) лежат в одной плоскости (ADK) , то и точка (Q) будет лежать в этой плоскости. Но еще (по построению) точка (Q) должна лежать в плоскости (ABC) , следовательно, она лежит на линии пересечения этих плоскостей, а это – (AK) .
Значит, прямая (AK) и есть проекция прямой (MN) на плоскость (ABC) . (L) – точка пересечения этих прямых.
2) Заметим, что для того, чтобы правильно нарисовать чертеж, необходимо найти точное положение точки (L) (например, на нашем чертеже точка (L) лежит вне отрезка (OK) , хотя она могла бы лежать и внутри него; а как правильно?).
Т.к. по условию сторона основания равна высоте пирамиды, то обозначим (AB=DO=a) . Тогда медиана (AK=dfrac2a) . Значит, (OK=dfrac13AK=dfrac 1a) . Найдем длину отрезка (OL) (тогда мы сможем понять, внутри или вне отрезка (OK) находится точка (L) : если (OL>OK) – то вне, иначе – внутри).
а) (triangle AMQsim triangle ADO) по двум углам ( (angle Q=angle O=90^circ, angle A) – общий). Значит,
[dfrac=dfrac=dfrac=dfrac 45 Rightarrow MQ=dfrac 45a, AQ=dfrac 45cdot dfrac 1a]
Значит, (QK=dfrac2a-dfrac 45cdot dfrac 1a=dfrac7a) .
б) Обозначим (KL=x) .
(triangle LMQsim triangle LNO) по двум углам ( (angle Q=angle O=90^circ, angle L) – общий). Значит,
Следовательно, (OL>OK) , значит, точка (L) действительно лежит вне отрезка (AK) .
Замечание
Не стоит пугаться, если при решении подобной задачи у вас получится, что длина отрезка отрицательная. Если бы в условиях предыдущей задачи мы получили, что (x) – отрицательный, это как раз значило бы, что мы неверно выбрали положение точки (L) (то есть, что она находится внутри отрезка (AK) ).
Пример 3
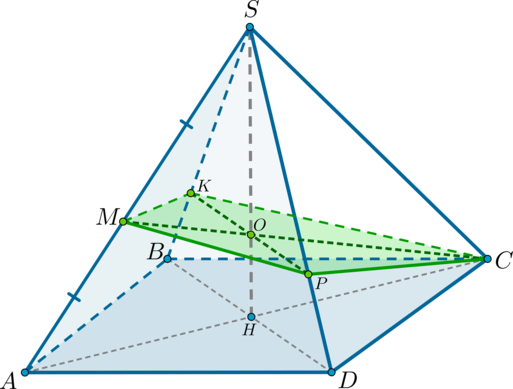
Дана правильная четырехугольная пирамида (SABCD) . Найдите сечение пирамиды плоскостью (alpha) , проходящей через точку (C) и середину ребра (SA) и параллельной прямой (BD) .
Решение
1) Обозначим середину ребра (SA) за (M) . Т.к. пирамида правильная, то высота (SH) пирамиды падает в точку пересечения диагоналей основания. Рассмотрим плоскость (SAC) . Отрезки (CM) и (SH) лежат в этой плоскости, пусть они пересекаются в точке (O) .
Для того, чтобы плоскость (alpha) была параллельна прямой (BD) , она должна содержать некоторую прямую, параллельную (BD) . Точка (O) находится вместе с прямой (BD) в одной плоскости – в плоскости (BSD) . Проведем в этой плоскости через точку (O) прямую (KPparallel BD) ( (Kin SB, Pin SD) ). Тогда, соединив точки (C, P, M, K) , получим сечение пирамиды плоскостью (alpha) .
2) Найдем отношение, в котором делят точки (K) и (P) ребра (SB) и (SD) . Таким образом мы полностью определим построенное сечение.
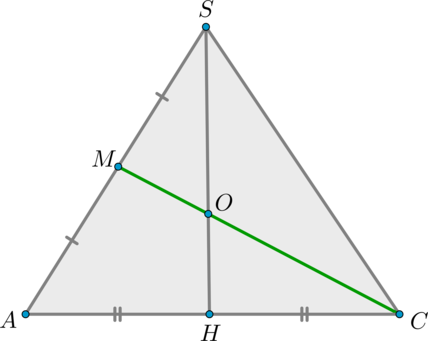
Заметим, что так как (KPparallel BD) , то по теореме Фалеса (dfrac=dfrac) . Но (SB=SD) , значит и (SK=SP) . Таким образом, можно найти только (SP:PD) .
Рассмотрим (triangle ASC) . (CM, SH) – медианы в этом треугольнике, следовательно, точкой пересечения делятся в отношении (2:1) , считая от вершины, то есть (SO:OH=2:1) .
Теперь по теореме Фалеса из (triangle BSD) : (dfrac=dfrac=dfrac21) .
3) Заметим, что по теореме о трех перпендикулярах (COperp BD) как наклонная ( (OH) – перпендикуляр на плоскость (ABC) , (CHperp BD) – проекция). Значит, (COperp KP) . Таким образом, сечением является четырехугольник (CPMK) , диагонали которого взаимно перпендикулярны.
Пример 4
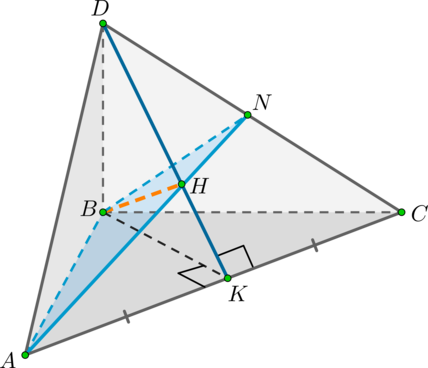
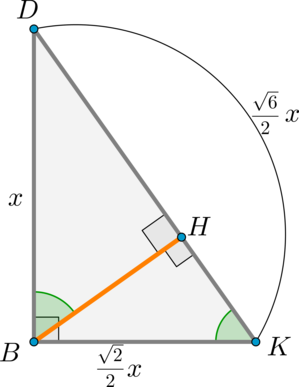
Дана прямоугольная пирамида (DABC) с ребром (DB) , перпендикулярным плоскости (ABC) . В основании лежит прямоугольный треугольник с (angle B=90^circ) , причем (AB=DB=CB) . Проведите через прямую (AB) плоскость, перпендикулярную грани (DAC) , и найдите сечение пирамиды этой плоскостью.
Решение
1) Плоскость (alpha) будет перпендикулярна грани (DAC) , если она будет содержать прямую, перпендикулярную (DAC) . Проведем из точки (B) перпендикуляр на плоскость (DAC) — (BH) , (Hin DAC) .
Проведем вспомогательные (BK) – медиану в (triangle ABC) и (DK) – медиану в (triangle DAC) .
Т.к. (AB=BC) , то (triangle ABC) – равнобедренный, значит, (BK) – высота, то есть (BKperp AC) .
Т.к. (AB=DB=CB) и (angle ABD=angle CBD=90^circ) , то (triangle ABD=triangle CBD) , следовательно, (AD=CD) , следовательно, (triangle DAC) – тоже равнобедренный и (DKperp AC) .
Применим теорему о трех перпендикулярах: (BH) – перпендикуляр на (DAC) ; наклонная (BKperp AC) , значит и проекция (HKperp AC) . Но мы уже определили, что (DKperp AC) . Таким образом, точка (H) лежит на отрезке (DK) .
Соединив точки (A) и (H) , получим отрезок (AN) , по которому плоскость (alpha) пересекается с гранью (DAC) . Тогда (triangle ABN) – искомое сечение пирамиды плоскостью (alpha) .
2) Определим точное положение точки (N) на ребре (DC) .
Обозначим (AB=CB=DB=x) . Тогда (BK) , как медиана, опущенная из вершины прямого угла в (triangle ABC) , равна (frac12 AC) , следовательно, (BK=frac12 cdot sqrt2 x) .
Рассмотрим (triangle BKD) . Найдем отношение (DH:HK) .
Заметим, что т.к. (BHperp (DAC)) , то (BH) перпендикулярно любой прямой из этой плоскости, значит, (BH) – высота в (triangle DBK) . Тогда (triangle DBHsim triangle DBK) , следовательно
[dfrac=dfrac Rightarrow DH=dfrac3x Rightarrow HK=dfrac6x Rightarrow DH:HK=2:1]
Рассмотрим теперь (triangle ADC) . Медианы треугольника точной пересечения делятся в отношении (2:1) , считая от вершины. Значит, (H) – точка пересечения медиан в (triangle ADC) (т.к. (DK) – медиана). То есть (AN) – тоже медиана, значит, (DN=NC) .
🌟 Видео
Как строить сеченияСкачать

Как строить сечения тетраэдра и пирамидыСкачать

Как строить сечения параллелепипедаСкачать

ВСЕ О СЕЧЕНИЯХ В СТЕРЕОМЕТРИИСкачать

№194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертежногоСкачать

Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Определение истинной величины треугольника АВС. Метод плоско-параллельного перемещенияСкачать

Задача, которую боятсяСкачать

Параллельные прямые | Математика | TutorOnlineСкачать

Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

ПОСТРОЕНИЕ СЕЧЕНИЙ ТЕТРАЭДРА ПЛОСКОСТЬЮСкачать

Построение следов плоскостиСкачать

Построение натуральной величины треугольника методом вращенияСкачать

Определение натуральной величины треугольника АВС методом вращения вокруг горизонтали или фронталиСкачать

Построение сечений Занятие 1Скачать
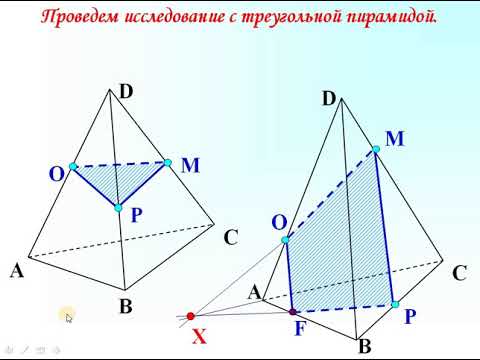
№3. Как строить сечения пирамидСкачать

Геометрия. Построение сечений.Метод параллельного переноса секущей плоскости.Скачать