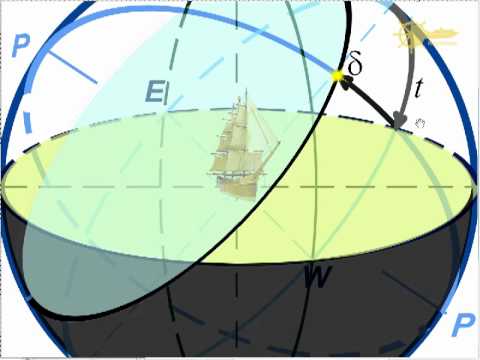
Параллактический треугольник в астрономии

• Параллактический треугольник (навигационный треугольник, PZX-треугольник) — в астронавигации сферический треугольник на небесной сфере, вершинами которого являются полюс (P), зенит (Z), и какое-либо выбранное светило (X). Другими словами, параллактический треугольник образован взаимным пересечением небесного меридиана, круга высоты и круга склонения.

Сторонами треугольника служат дуги PZ = 90° — φ, ZR = z и PR = 90° — δ, где φ — широта на которой находится наблюдатель, z — зенитное расстояние светила, а δ — его склонение.

Углы треугольника в свою очередь: при вершине Z = 180° — A, где A — это азимут, при вершине P = t, то есть равен часовому углу и третий угол, при светиле R, обозначается q и называется параллактический угол.

Конфигурация параллактического треугольника зависит от широты, на которой находится наблюдатель, и от времени.

Связанные понятия

В математике и физике барице́нтр, или геометри́ческий центр, двумерной области — это среднее арифметическое положений всех точек фигуры. Определение распространяется на любой объект в n-мерном пространстве — барицентр является средним положением всех точек фигуры по всем координатным направлениям. Неформально — это точка равновесия фигуры, вырезанной из картона в предположении, что картон имеет постоянную плотность и гравитационное поле постоянно по величине и направлению.

Видео:2. Параллактический треугольник.mp4Скачать

Please wait.

Видео:2 Параллактический треугольник. Мореходная астрономия. НавигацияСкачать

We are checking your browser. gufo.me

Видео:3 Параллактический треугольник (реклама)Скачать

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

Видео:9 класс. Определение расстояний в астрономии методом параллаксаСкачать

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6d439e722ab15ab2 • Your IP : 85.95.179.65 • Performance & security by Cloudflare

Видео:1. Построение небесной сферы .mp4Скачать

Астрометрия и геодезическая астрономия (стр. 2 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9

Большой круг ZsZ’, по которому вертикальная плоскость, проходящая через светило s, пересекает небесную сферу, называется вертикалом или кругом высот светила.

Большой круг PNsPS, проходящий через светило перпендикулярно небесному экватору, называется кругом склонения светила.

Малый круг nsn’, проходящий через светило параллельно небесному экватору, называется суточной параллелью. Видимое суточное движение светил происходит вдоль суточных параллелей.

Малый круг аsа’, проходящий через светило параллельно небесному горизонту, называется кругом равных высот, или альмукантаратом.

В первом приближении орбита Земли может быть принята за плоскую кривую — эллипс, в одном из фокусов которого находится Солнце. Плоскость эллипса, принимаемого за орбиту Земли, называется плоскостью эклиптики.

В сферической астрономии принято говорить о видимом годичном движении Солнца. Большой круг ЕgЕ’d, по которому происходит видимое движение Солнца в течение года, называется эклиптикой. Плоскость эклиптики наклонена к плоскости небесного экватора на угол, примерно равный 23.5 0.

На рис. 1.4. показаны:

g – точка весеннего равноденствия;

d – точка осеннего равноденствия;

Е – точка летнего солнцестояния; Е’ – точка зимнего солнцестояния; RNRS – ось эклиптики; RN — северный полюс эклиптики; RS — южный полюс эклиптики; e — наклон эклиптики к экватору.

1.1.2. Системы координат на небесной сфере

Для определения сферической системы координат на сфере выбирают два взаимно перпендикулярных больших круга, один из которых называют основным, а другой — начальным кругом системы.

В геодезической астрономии и астрометрии используются следующие системы сферических координат:

1) горизонтальная система координат;

2) первая и вторая экваториальные системы координат;

3) эклиптическая система координат.

Название систем обычно соответствует названию больших кругов, принятых за основной. Рассмотрим эти системы координат подробнее.

Горизонтальная система координат

Видео:2 Параллактический треугольник mp4Скачать

Видео:МОРСКАЯ НАВИГАЦИЯ | СФЕРИЧЕСКАЯ ТРИГОНОМЕТРИЯСкачать

Горизонтальная система координат изображена на рис.1.5.

Основной круг в этой системе —астрономический горизонт SMN. Его геометрические полюса — Z (зенит) и Z’ (надир).

Начальный круг системы — небесный меридиан ZSZ’N.

Начальная точка системы — точка юга S.

Определяющий круг системы — вертикал светила ZsZ’.

Первая координата горизонтальной системы – высота h, угол между плоскостью горизонта и направлением на светило ÐМОs, или дуга вертикала от горизонта до светила ÈMs. Высота отсчитывается от горизонта и может принимать значения

В геодезической астрономии, как правило, вместо высоты h используется зенитное расстояние z — угол между отвесной линией и направлением на светило ÐZОs, или дуга вертикала ÈZs. Зенитное расстояние есть дополнение до 900 высоты h:

Видео:Законы КеплераСкачать

Зенитное расстояние светила отсчитывается от зенита и может принимать значения

Вторая координата горизонтальной системы – азимут – двугранный угол SZZ’s между плоскостью небесного меридиана (начального круга) и плоскостью вертикала светила, обозначаемый буквой А:

А = двугр. угол SZZ’s = ÐSOM = ÈSM = сф. угол SZM.

В астрономии азимуты отсчитываются от точки юга S по ходу часовой стрелки в пределах

Вследствие суточного вращения небесной сферы горизонтальные координаты светила меняются в течение суток. Поэтому, фиксируя положение светил в этой системе координат, нужно отмечать момент времени, к которому относятся координаты h, z, A. Кроме того, горизонтальные координаты являются не только функциями времени, но и функциями положения места наблюдения на земной поверхности. Эта особенность горизонтальных координат обусловлена тем, что отвесные линии в разных точках земной поверхности имеют разное направление.

В горизонтальной системе координат ориентируются геодезические инструменты и выполняются измерения.

Первая экваториальная система координат

Первая экваториальная система координат представлена на рис.1.6.

Основной круг первой экваториальной системы координат есть небесный экватор Q’KQ. Геометрические полюса небесного экватора — северный и южный полюсы мира, РN и РS.

Начальный круг системы — небесный меридиан РNQ’РSQ.

Начальная точка системы – верхняя точка экватора Q.

Определяющий круг системы – круг склонения РNsРS.

Первая координата первой экваториальной системы — склонение светила d, угол между плоскостью небесного экватора и направлением на светило ÐКОs, или дуга круга склонения ÈКs. Склонение отсчитывается от экватора к полюсам и может принимать значения

Иногда используется величина D = 900 — d, где 00 £ D £1800, называемая полярным расстоянием.

Склонение не зависит ни от суточного вращения Земли, ни от географических координат пункта наблюдения f, l.

Вторая координата первой экваториальной системы — часовой угол светила t — двугранный угол между плоскостями небесного меридиана и круга склонения светила, или сферический угол при северном полюсе мира:

t =дв. угол QРNРSs = сф. угол QРNs = ÈQК = ÐQOK.

Часовой угол отсчитывается от верхней точки экватора Q в направлении суточного вращения небесной сферы (по ходу часовой стрелки) от 01.01.01, как правило, в часовой мере,

Градусы и часы связаны соотношениями:

3600 = 24h, 150 = 1h, 15′ = 1m, 15″ = 1s.

Вследствие видимого суточного движения небесной сферы часовые углы светил постоянно изменяются. Часовой угол t отсчитывается от небесного меридиана, положение которого определяется направлением отвеса (ZZ’) в данном пункте и, следовательно, зависит от географических координат пункта наблюдения на Земле.

Вторая экваториальная система координат

Вторая экваториальная система координат изображена на рис.1.7.

Основной круг второй экваториальной системы — небесный экватор QgQ’.

Начальный круг системы — круг склонений точки весеннего равноденствия РNgРS, называемый колюром равноденствий.

Начальная точка системы – точка весеннего равноденствия g.

Видео:Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Определяющий круг системы – круг склонения РNsРS.

Первая координата — склонение светила d.

Вторая координата — прямое восхождение a, двугранный угол между плоскостями колюра равноденствия и круга склонения светила, или сферический угол gРNs, или дуга экватора gК:

a =дв. угол gРNРSs = сф. угол gPNs = ÈgК = ÐgOK.

Прямое восхождение a выражается в часовой мере и отсчитывается от точки g против хода часовой стрелки в направлении, противоположном видимому суточному движению светил,

Во второй экваториальной системе координаты a и d не зависят от суточного вращения светил. Так как эта система не связана ни с горизонтом, ни с меридианом, то a и d не зависят от положения точки наблюдения на Земле, то есть от географических координат f и l.

При выполнении астрономо-геодезических работ координаты светил a и d должны быть известны. Они используются при обработке результатов наблюдений, а также для вычисления таблиц горизонтальных координат светил (A и h), называемых эфемеридами, с помощью которых можно отыскать астрономическим теодолитом светило в любой заданный момент времени. Экваториальные координаты светил a и d определяются из специальных наблюдений на астрономических обсерваториях и публикуются в звездных каталогах.

Эклиптическая система координат

Эклиптическая система координат изображена на рис.1.8.

Основной круг эклиптической системы — эклиптика ЕgЕ’.

Начальный круг системы — круг широты точки весеннего равноденствия RNgRS. Геометрические полюса небесного экватора — северный и южный полюсы эклиптики, RN и RS.

Начальная точка системы – точка весеннего равноденствия g.

Видео:АСТРОНОМИЯ ● ОСНОВЫ АСТРОНОМИИ ● ВСЕ ЛИНИИ НЕБЕСНОЙ СФЕРЫСкачать

Определяющий круг системы – круг широты РNsРS.

Первая координата – эклиптическая широта b — угол между плоскостью эклиптики и направлением на светило ÐКОs, или дуга круга широты ÈКs. Эклиптическая широта отсчитывается от экватора к полюсам и может принимать значения

Вторая координата – эклиптическая долгота l, двугранный угол между плоскостями кругов широты точки g и светила s, или сферический угол gRNs, или дуга эклиптики gК:

l =дв. угол gRNRSs = сф. угол gRNs = ÈgК = ÐgOK.

Эклиптическая долгота l отсчитывается от точки g в направлении видимого годичного движения Солнца,

Эклиптические широты и долготы не изменяются от суточного вращения небесной сферы. Эклиптическая система координат широко используется в теоретической астрономии и небесной механике в теории движения тел солнечной системы. Так как Луна и планеты движутся вблизи плоскости эклиптики, то в эклиптической системе координат заметно упрощается учет возмущений их орбит.

В звездной астрономии используют галактическую систему координат, где основной круг – галактический экватор – большой круг, наиболее совпадающий с серединой Млечного пути. Координаты звезд в этой системе задаются галактической широтой и галактической долготой.

1.1.3. Географические координаты точек на поверхности Земли

Если спроектировать точку М земной поверхности на небесную сферу по направлению отвесной линии ZZ’ (рис.1.9.), то сферические координаты зенита Z этой точки называются географическими координатами: географической широтой f и географической долготой l.

Широта и долгота точек на поверхности Земли задаются относительно земного экватора и начального меридиана.

Земным экватором называется плоскость, перпендикулярная оси вращения Земли. Ось вращения Земли непрерывно совершает колебания (см. раздел “Движение земных полюсов”), поэтому различают мгновенную ось вращения (мгновенный экватор) и среднюю ось вращения (средний экватор).

Плоскость астрономического меридиана, проходящего через произвольную точку земной поверхности, содержит отвесную линию в данной точке и параллельна оси вращения Земли.

Начальный меридиан проходит через центральную точку фундаментального астрометрического инструмента Гринвичской обсерватории (согласно международному соглашению 1883г).

Начальная точка, от которой ведется счет долгот, есть точка пересечения начального меридиана с плоскостью экватора.

В геодезической астрономии определяются астрономические широта и долгота, f и l, а также астрономический азимут направления A.

Астрономическая широта f есть угол между плоскостью экватора и отвесной линией в данной точке. Широта отсчитывается от экватора к северному полюсу от 00 до +900 и к южному полюсу от 00 до -900.

Астрономическая долгота l – двугранный угол между плоскостями начального и текущего астрономических меридианов. Долгота отсчитывается от гринвичского меридиана к востоку (lE- восточная долгота) и к западу (lW — западная долгота) от 01.01.01 или, в часовой мере, от 0 до 12 часов (12h). Иногда долготу считают в одну сторону от 0 до 3600 или, в часовой мере, от 0 до 24 часов.

Астрономический азимут направления А – двугранный угол между плоскостью астрономического меридиана и плоскостью, проходящей через отвесную линию и точку, на которую измеряется направление.

Если астрономические координаты связаны с отвесной линией и осью вращения Земли, то геодезические – с поверхностью относимости (эллипсоидом) и с нормалью к этой поверхности. Подробно геодезические координаты рассматриваются в разделе “Высшая геодезия”.

1.1.4. Связь между различными системами координат

Связь между координатами первой и второй

экваториальных систем. Формула звездного времени

В первой и второй экваториальных системах склонение d измеряется одним и тем же центральным углом и одной и той же дугой большого круга, значит, в этих системах d одно и то же. Рассмотрим связь между t и a. Для этого определим часовой угол точки g — ее положение в первой экваториальной системе координат:

Из рис.1.10. видно, что для любого светила справедливо равенство

Часовой угол точки весеннего равноденствия является мерой звездного времени s:

Последняя формула называется формулой звездного времени: сумма часового угла и прямого восхождения светила равна звездному времени.

Связь между небесными и географическими координатами

Теорема 1. Географическая широта места наблюдения численно равна склонению зенита в точке наблюдения и равна высоте полюса мира над горизонтом:

Доказательство следует из рис.1.11. Географическая широта f есть угол между плоскостью земного экватора и отвесной линией в пункте наблюдения, ÐMoq. Склонение зенита dz есть угол между плоскостью небесного экватора и отвесной линией, ÐZMQ. Склонение зенита и широта равны как соответствующие углы при параллельных прямых. Высота полюса Мира, hp=ÐPNMN, и склонение зенита dz равны между собой как углы между взаимно перпендикулярными сторонами. Итак, теорема 1 устанавливает связь координат географической, горизонтальной и экваториальной систем. Она положена в основу определения географических широт пунктов наблюдения.

Теорема 2. Разность часовых углов одного и того же светила, измеренная в один и тот же физический момент времени в двух различных точках земной поверхности численно равна разности географических долгот этих точек на земной поверхности:

Видео:Параллакс наблюдаемых звёзд (видео 14) | Звёзды, чёрные дыры и галактики | Космология и астрономияСкачать

Доказательство следует из рисунка 1.9., на котором показаны Земля и описанная вокруг нее небесная сфера. Разность долгот двух пунктов есть двугранный угол между меридианами этих пунктов; разность часовых углов светила s есть двугранный угол между двумя небесными меридианами этих пунктов. В силу параллельности небесных и земных меридианов, теорема доказана.

Вторая теорема сферической астрономии положена в основу определения долгот пунктов.

Параллактический треугольник

Параллактический треугольник – сферический треугольник с вершинами Pn, Z, s (рис.1.12.). Он образован пересечением трех больших кругов: небесного меридиана, круга склонения и вертикала светила.

Угол q между вертикалом светила и кругом склонения называется параллактическим.

Элементы параллактического треугольника относятся к трем системам координат: горизонтальной (А, z), первой экваториальной (d, t) и географической (f). Связь между этими системами координат может быть установлена через решение параллактического треугольника.

Дано: в момент звездного времени s в пункте с известной широтой f наблюдается светило s с известными экваториальными координатами a и d.

Задача: определить горизонтальные координаты: азимут A и зенитное расстояние z.

Решение задачи выполняется по формулам сферической тригонометрии. Формулы косинусов, синусов и пяти элементов применительно к параллактическому треугольнику записываются следующим образом:

Разделив формулу (1.3) на (1.2), получим:

сtg A = sin f ctg t — tg d cos f cosec t. (1.4)

Формулы (1.1) и (1.4) являются уравнениями связи в зенитальных и азимутальных способах астрономических определений, соответственно.

1.1.5. Видимое суточное вращение небесной сферы

Виды суточного движения звезд

Видимое суточное вращение небесной сферы происходит с востока на запад и обусловлено вращением Земли вокруг оси. При этом светила перемещаются по суточным параллелям. Вид суточного движения относительно горизонта данного пункта с широтой f зависит от склонения светила d. По виду суточного движения светила бывают:

1) незаходящие,

d> dN, или d > 900 — f,

2) имеющие восход и заход,

5) пересекающие первый вертикал,

— dZ £ d £ dZ, или — f £ d £ f.

На рис.1.13. показаны области, где находятся суточные параллели звезд, удовлетворяющие по виду суточного движения указанным выше условиям.

Прохождение светил через меридиан. Кульминации.

Момент прохождения светила через меридиан называют кульминацией. В момент верхней кульминации светило занимает самое высокое положение относительно горизонта, в момент нижней кульминации светило находится в самом нижнем положении относительно горизонта. Нарисуем чертеж небесной сферы в проекции на меридиан (рис.1.14.). Для всех светил в верхней кульминации часовой угол t = 0h, а в нижней t = 12h. Поэтому в верхней кульминации s = a, а в нижней s=a+12h.

Горизонтальные координаты A, z светил в кульминациях вычисляются по следующим формулам.

Верхняя кульминация (ВК):

a) светило кульминирует к югу от зенита,

(-900 d > f), суточная параллель 1,

А = 1800, z = d — f.

а) светило кульминирует к северу от надира, (900 > d > — f), суточные параллели 1 и 2,

А = 1800, z = 1800 – (f + d);

б) светило кульминирует к югу от надира, (-900 0, для светила с положительным склонением (d>0) cost 0 и cosA>0, поэтому

для захода tW= t1, AW = A1,

для восхода tE=24h — t1, AE = 3600 — A1.

В каждом случае моменты восхода и захода по звездному времени будут

sW = a + tW, sE = a + tE.

Полученные формулы используются для расчета обстоятельств восхода и захода Солнца, планет, Луны и звезд.

Прохождение светил через первый вертикал

Положению светила в первом вертикале соответствует прямоугольный параллактический треугольник (рис.1.16), который решается с использованием правила Модюи-Непера:

Для северного полушария Земли (f>0), для светила с положительным склонением (d>0) cost >0,

следовательно, часовые углы светила в моменты прохождения западной и восточной частей вертикала будут

tW= t1, tE=24h — t1 .

При отрицательном склонении (d 900, следовательно, светило проходит первый вертикал под горизонтом.

Согласно формуле звездного времени моменты прохождения светилом первого вертикала будут

sW = a + tW, sE = a + tE.

Азимуты светила в первом вертикале есть AW = 900, AE = 2700, если отсчет ведется по часовой стрелке от точки Юга.

В геодезической астрономии есть ряд способов астрономических определений географических координат, основывающихся на наблюдении светил в первом вертикале. Формулы связи между горизонтальными и экваториальными координатами светила в первом вертикале используются при составлении рабочих эфемерид и для обработки наблюдений.

Вычисление горизонтальных координат и звездного времени

для светил в элонгации

В моменты элонгации вертикал светила имеет общую с суточной параллелью касательную прямую, то есть, видимое суточное движение светила происходит вдоль его вертикала. Поскольку круг склонений всегда пересекает суточную параллель под прямым углом, то параллактический угол PNsZ становится прямым. Решая прямоугольный параллактический треугольник по правилу Модюи-Непера, можно найти выражения для t, z, A:

Для западной элонгации

AW = 1800 – A1, tW = t1, sW = a + tW,

для восточной элонгации

AE = 1800 + A1, tE = — t1, sE = a + tE.

Наблюдение светил в элонгациях выполняют при исследованиях астрономических теодолитов в полевых условиях.

1.1.6. Составление эфемерид светил. Эфемерида Полярной звезды

Эфемеридой светила называется таблица его координат, в которой аргументом служит время. В геодезической астрономии часто составляют эфемериды в горизонтальной системе координат (z, A) с точностью ± 1′. Такие эфемериды называют рабочими. Рабочие эфемериды звезд с координатами (z, A) составляются на период наблюдений для того, чтобы легко и быстро находить звезду на небесной сфере с помощью астрономического прибора.

При полевых астрономических наблюдениях в северном полушарии для ориентирования инструмента часто используются наблюдения Полярной звезды.

Составление эфемерид Полярной выполняется в следующем порядке.

В пункте с широтой f для наблюдения звезды с координатами a, d на промежуток времени от s1 до sk требуется составить таблицу значений A и z.

Полярное расстояние Полярной D не превышает 10. Поэтому параллактический треугольник представляет собой узкий сферический треугольник (рис.1.17.). Опустим из светила сферический перпендикуляр sK на меридиан. Получим два прямоугольных треугольника, PNKs (элементарный) и KsZ (узкий). Решая треугольник PNKs как плоский, можно записать

PNK = f = Dcos t, sK = x = Dsin t, где t = s-a.

Рассмотрим решение прямоугольного треугольника KsZ. В нем известны две стороны, KZ = 900-(f+f) и Ks = x. По правилу Модюи-Непера

Для вычисления z с ошибкой 1′ можно принять 1/cosA ≈1, тогда

z = 900-(f+f), или h = f + f.

Из треугольника KsZ

или в виду малости x и AN при вычислении азимута с точностью до 1′ можно записать

x = AN sin z = AN cos(f+f).

Азимут AN отсчитывается от точки севера N. Азимуты Полярной, отсчитанные от точки юга S, определяются по формулам

Контрольные вопросы к разделу 1.1

1. Как определяются направления отвесной линии и оси Мира?

2. Что такое эклиптика, точка гамма?

3. Назвать параметры (основной, начальный и определяющий круги, начальную точку и полюса) горизонтальной, экваториальных и эклиптической систем координат.

4. В чем принципиальное отличие астрономических и геодезических координат точек на Земле?

5. В каких случаях используются горизонтальная, экваториальные и эклиптическая системы координат?

6. Сформулируйте теоремы, положенные в основу определения географических широт и долгот пунктов.

7. Чему равны азимут, высота, часовой угол и склонение основных точек небесной сферы в пункте с широтой f?

8. В каком случае формулы решения параллактического треугольника не применимы?

9. Изобразить параллактические треугольники для светил, пересекающих горизонт, первый вертикал в западной и восточной половинах небесной сферы.

10. На каком зенитном расстоянии будет Сириус (склонение = -160) в верхней кульминации в Новосибирске (широта равна 550)?

11. На сколько отличаются высоты светил в верхней и нижней кульминации для наблюдателя, находящегося на полюсе Земли?

12. Чему равно склонение звезды, проходящей Новосибирске через зе­нит? (Широта Новосибирска 550).

13. Что такое эфемериды звезд и для чего они нужны?

1.2. Измерение времени в астрономии

Одной из задач геодезической астрономии, астрометрии и космической геодезии является определение координат небесных тел в заданный момент времени. Построением астрономических шкал времени занимаются национальные службы времени и Международное бюро времени.

В основе всех известных способов построения непрерывных шкал времени лежат периодические процессы, например:

— вращение Земли вокруг своей оси;

— обращение Земли вокруг Солнца по орбите;

— обращение Луны вокруг Земли по орбите;

— качание маятника под действием силы тяжести;

— упругие колебания кристалла кварца под действием переменного тока;

— электромагнитные колебания молекул и атомов;

— радиоактивный распад ядер атомов и другие процессы.

Систему времени можно задать следующими параметрами:

1) механизм – явление, обеспечивающее периодически повторяющийся процесс (например, суточное вращение Земли);

2) масштаб – промежуток времени, за который повторяется процесс;

3) начальная точка, нульпункт – момент начала повторения процесса;

4) способ отсчета времени.

В геодезической астрономии, астрометрии, небесной механике используются системы звездного и солнечного времени, основанные на вращении Земли вокруг оси. Это периодическое движение является в высшей степени равномерным, не ограниченным во времени и непрерывным на протяжении всего существования человечества.

Кроме того, в астрометрии и небесной механике используются

— системы эфемеридного и динамического времени, как идеальное построение равномерной шкалы времени;

— система атомного времени – практическая реализация идеально равномерной шкалы времени.

1.2.2. Звездное время

Звездное время обозначается s. Параметрами системы звездного времени являются:

1) механизм – вращение Земли вокруг своей оси;

2) масштаб — звездные сутки, равные промежутку времени между двумя пос­ледовательными верхними кульминациями точки весеннего равноденствия в пункте наблюдения;

3) начальная точка на небесной сфере — точка весен­него равноденствия g, нульпункт (начало звездных суток) — момент верх­ней кульминации точки g;

4) способ отсчета. Мера измерения звездного времени — часовой угол точки весеннего равноденствия, tg. Измерить его невозможно, но для любой звезды справедливо выражение

следовательно, зная прямое восхождение звезды a и вычисляя ее часовой угол t, можно определить звездное время s.

Различают истинную, среднюю и квазиистинную точки гамма (разделение связано астрономическим фактором нутацией, см. пункт 1.3.9), относительно которых измеряется истинное, среднее и квазиистинное звездное время.

Система звездного времени применяется при определении географических координат пунктов на поверхности Земли и азимутов направления на земные предметы, при изуче­нии неравномерностей суточного вращения Земли, при установлении нуль­пунктов шкал других систем измерения времени. Эта система, хоть и широко применяется в астрономии, в повседневной жизни неудобна. Смена дня и ночи, обусловленная видимым суточным движением Солнца, создает вполне определенный цикл в деятельности человека на Земле. Поэтому издавна счисление времени ведется по суточному движению Солнца.

1.2.3. Истинное и среднее солнечное время. Уравнение времени

Система истинного солнечного времени (или истинное солнечное время — m¤) применяется при астрономических или геодезических наблюдениях Солнца. Параметры системы:

1) механизм — вращение Земли вокруг своей оси;

2) масштаб — истинные солнечные сутки — промежуток времени между двумя последовательными нижними кульминациями центра истинного Солнца;

3) начальная точка — центр диска истинного Солнца — ¤, нульпункт — истинная полночь, или момент нижней кульминации центра диска истинного Солнца;

4) способ отсчета. Мера измерения истинного солнечного времени — геоцентрический часовой угол истинного Солнца t¤ плюс 12 часов:

Единица истинного солнечного времени — секунда, равная 1/86400 истинных солнечных суток, не удовлетворяет основному требованию, предъявляемому к единице измерения времени — она не постоянна.

Причинами непостоянства шкалы истинного солнечного времени являются:

1) неравномерное движение Солнца по эклиптике вследствие эллиптичности орбиты Земли;

2) неравномерное возрастание прямого восхождения Солнца в течение года, так как Солнце по эклиптике, наклоненной к небесному экватору под углом примерно 23.50.

Вследствие этих причин применение системы истинного солнечного времени на практике неудобно. Переход к равномерной шкале солнечного времени происходит в два этапа [3].

Этап 1 — переход к фиктивному среднему эклиптическому Солнцу. На данном этапе исключается неравномерность движения Солнца по эклиптике. Неравномерное движение по эллиптической орбите заменяется равномерным движением по круговой орбите. Истинное Солнце и среднее эклиптическое Солнце совпадают, когда Земля проходит через перигелий и афелий своей орбиты.

Этап 2 — переход к среднему экваториальному Солнцу, движущемуся равномерно вдоль небесного экватора. Здесь исключается неравномерность возрастания прямого восхождения Солнца, обусловленная наклоном эклиптики. Истинное Солнце и среднее экваториальное Солнце одновременно проходят точки весеннего и осеннего равноденствия.

В результате перечисленных действий вводится новая система измерения времени – среднее солнечное время.

Среднее солнечное время обозначается m. Параметрами системы среднего солнечного времени являются:

1) механизм — вращение Земли вокруг оси;

2) масштаб — средние сутки — промежуток времени между двумя последовательными нижними кульминациями среднего экваториального Солнца ¤экв;

3) начальная точка — среднее экваториальное Солнце ¤экв, нульпункт — средняя полночь, или момент нижней кульминации среднего экваториального Солнца;

4) способ отсчета. Мерой измерения среднего времени является геоцентрический часовой угол среднего экваториального Солнца t¤экв плюс 12 часов.

Определить среднее солнечное время непосредственно из наблюдений нельзя, так как среднее экваториальное Солнце – фиктивная точка на небесной сфере. Среднее солнечное время вычисляют по истинному солнечному времени, определенному из наблюдений истинного Солнца. Разность истинного солнечного времени m¤ и среднего солнечного времени m называется уравнением времени и обозначается h:

h = m¤ — m = t¤ — t¤ ср. экв..

Уравнение времени выражается двумя синусоидами с годовым и полугодовым периодами:

h = h1 + h2 » -7.7msin (l + 790)+ 9.5m sin 2l,

где l – эклиптическая долгота среднего эклиптического Солнца.

График h есть кривая с двумя максимумами и двумя минимумами, которая в декартовой прямоугольной системе координат имеет вид, показанный на рис. 1.18.

Рис.1.18. График уравнения времени

Значения уравнения времени лежат в пределах от +14m до –16m.

В Астрономическом Ежегоднике на каждую дату приводится величина Е, равная

С данной величиной связь между средним солнечным временем и часовым углом истинного Солнца определяется выражением

При точном определении численного значения промежутка времени, заключенного между двумя отдаленными датами удобно пользоваться непрерывным счетом суток, которые в астрономии называют юлианскими днями.

Начало счета юлианских дней – средний гринвичский полдень 1 января 4713 г. до н. э., от начала этого периода ведется счет и нумерация средних солнечных суток так, что каждой календарной дате соответствует определенный юлианский день, обозначаемый кратко JD. Так, эпохе 1900,январь 0,12hUT соответствует юлианская дата JD 2415020.0, а эпохе 2000, январь 1, 12hUT — JD2451545.0.

1 юлианский год содержит 365,25 средних солнечных суток (средняя продолжительность года в юлианском летоисчислении), юлианское столетие – 36 525 средних солнечных суток.