Отрезок сд высота прямоугольного треугольника

Видео:8 класс, 26 урок, Пропорциональные отрезки в прямоугольном треугольникеСкачать

Ваш ответ

Видео:№576. Высота прямоугольного треугольника, проведенная из вершины прямого угла, делитСкачать

решение вопроса

Видео:Высота в прямоугольном треугольнике. 8 класс.Скачать

Похожие вопросы

• Все категории
• экономические 43,287
• гуманитарные 33,620
• юридические 17,900
• школьный раздел 607,113
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:8 класс, 19 урок, Пропорциональные отрезкиСкачать

Отрезок сд высота прямоугольного треугольника

Вопрос по геометрии:

Отрезок CD- высота прямоуг. треугольника ABC, проведенная из вершины прямоугольного угла C. Найдите радиус окружности с центром A, которая касается прямой CD,если CD=4,AB=12.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Пусть радиус равен R.

Треуогльник ВСD подобен треугольнику CDA.

Решаем это квадратное уравнение.

2 ответа и будут двумя решениями.

Дискриминант = 144-64 = 80

или = 12+9/2 = 21/2 =10.5

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:пропорциональные отрезки в ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ 8 классСкачать

Свойства высоты прямоугольного треугольника

В данной публикации мы рассмотрим основные свойства высоты в прямоугольном треугольнике, а также разберем примеры решения задач по этой теме.

Примечание: треугольник называется прямоугольным, если один из его углов является прямым (равняется 90°), а два остальных – острые ( Содержание скрыть

Видео:Геометрия 8 класс (Урок№19 - Пропорциональные отрезки в прямоугольном треугольнике.)Скачать

Свойства высоты в прямоугольном треугольнике

Свойство 1

В прямоугольном треугольнике две высоты (h₁ и h₂) совпадают с его катетами.

Третья высота (h₃) опускается на гипотенузу из прямого угла.

Свойство 2

Ортоцентр (точка пересечения высот) прямоугольного треугольника находится в вершине прямого угла.

Свойство 3

Высота в прямоугольном треугольнике, проведенная к гипотенузе, делит его на два подобных прямоугольных треугольника, которые также подобны исходному.

Аналогичным образом доказывается, что ∠ABD = ∠DAC.

Свойство 4

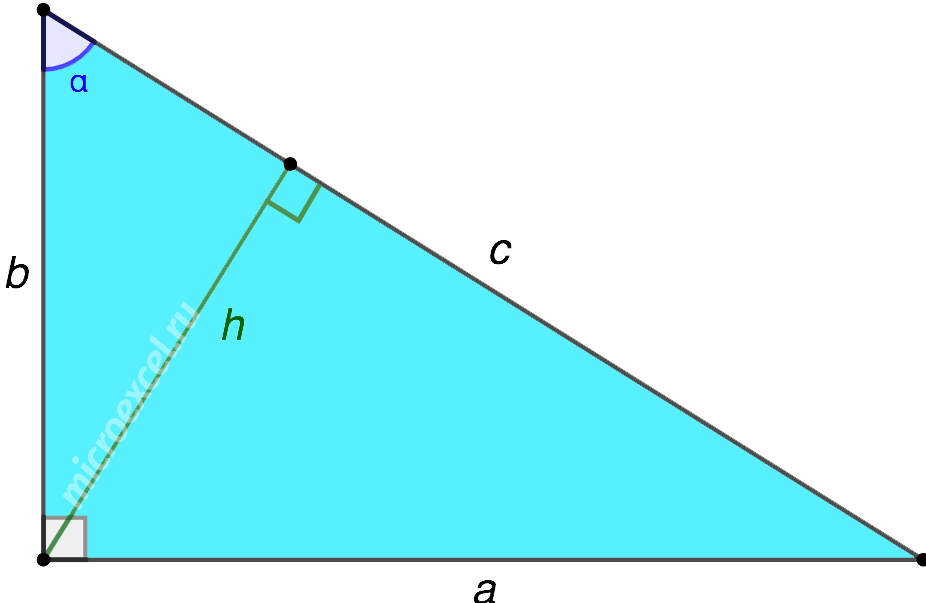
В прямоугольном треугольнике высота, проведенная к гипотенузе, вычисляется следующим образом:

1. Через отрезки на гипотенузе, образованные в результате ее деления основанием высоты:

2. Через длины сторон треугольника:

Данная формула получена из Свойства синуса острого угла в прямоугольном треугольнике (синус угла равен отношению противолежащего катета к гипотенузе) :

Примечание: к прямоугольному треугольнику, также, применимы общие свойства высоты, представленные в нашей публикации – “Высота в треугольнике abc: определение, виды, свойства”.

Видео:КАТЕТЫ И ВЫСОТА В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ ЧАСТЬ I #математика #егэ #огэ #Shorts #геометрияСкачать

Пример задачи

Задача 1
Гипотенуза прямоугольного треугольника поделена высотой, проведенной к ней, на отрезки 5 и 13 см. Найдите длину этой высоты.

Решение
Воспользуемся первой формулой, представленной в Свойстве 4:

Задача 2
Катеты прямоугольного треугольника равны 9 и 12 см. Найдите длину высоты, проведенной к гипотенузе.

Решение
Для начала найдем длину гипотенузы по теореме Пифагора (пусть катеты треугольника – это “a” и “b”, а гипотенуза – “c”):
c 2 = a 2 + b 2 = 9 2 + 12 2 = 225.
Следовательно, с = 15 см.

Теперь можно применить вторую формулу из Свойства 4, рассмотренного выше:

📽️ Видео

Математика | Метрические соотношения в прямоугольном треугольникеСкачать

8 класс Геометрия. Метрические соотношения в прямоугольном треугольнике. Высота к гипотенузе Урок #7Скачать

Геометрические задачи, которые точно БУДУТ НА ОГЭ! / Решаем 23 задание на ОГЭ 2023 по математикеСкачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

62 Пропорц отрезки в прямоуг треугольникеСкачать

Высота как среднее геометрическое отрезков | Профильная математикаСкачать

Высота AH ромба ABCD делит сторону CD на отрезки DH = 20 и CH = 5. Найдите высоту ромба.Скачать

Пропорциональные отрезки в прямоугольном треугольникеСкачать

№205. Через вершину С прямого угла прямоугольного треугольника ABC проведена прямая CD, перпендикуляСкачать

Высота в прямоугольном треугольнике. Соотношения в прямоугольном треугольнике.Скачать

Пропорциональные отрезки в прямоугольном треугольнике | Геометрия 7-9 класс #63 | ИнфоурокСкачать

Свойство высоты в прямоугольном треугольникеСкачать

ГЕОМЕТРИЯ 8 класс : Пропорциональные отрезки в прямоугольном треугольникеСкачать