Отрезки вероятность построить треугольник (3 видео)

Найти вероятность того, что из трех наудачу взятых отрезков длиной не более L можно построить треугольник. Предполагается

Содержание

Ваш ответ
решение вопроса
Похожие вопросы
Даны отрезки длиной 2, 5, 6 и 10. Какова вероятность того, что из наудачу взятых 3 отрезков можно построить треугольник?
Описание и исходные данные задания, 50% решения + фотография:
Палку ломают случайным образом на 3 части.
Ответ
Решение задачи
О задаче
Скачать задачу
Оставить комментарий
Решите задачу
Занимательные задачи
📽️ Видео

Видео:SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать

Ваш ответ

Видео:Геометрическая вероятность. С какой вероятностью можно составить треугольникСкачать

решение вопроса

Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Даны отрезки длиной 2, 5, 6 и 10. Какова вероятность того, что из наудачу взятых 3 отрезков можно построить треугольник?

Готовое решение: Заказ №8390

Тип работы: Задача

Статус: Выполнен (Зачтена преподавателем ВУЗа)

Предмет: Теория вероятности

Дата выполнения: 29.08.2020

Цена: 208 руб.

Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

1. Даны отрезки длиной 2, 5, 6 и 10. Какова вероятность того, что из наудачу взятых 3 отрезков можно построить треугольник?

Решение.

В данном случае нам важен только состав выбранных отрезков (но не порядок выбора), то есть речь идёт о сочетаниях. Общее число различных способов выбора трёх отрезков равно числу сочетаний из 4-х элементов по 3 элемента:

У треугольника любая сторона должна быть меньше суммы двух других. Этому условию отвечают следующие наборы трёх чисел:

Если вам нужно решить математику, тогда нажмите ➔ заказать математику.

Похожие готовые решения:

Имеется 6 отрезков, длины которых равны соответственно 2, 4, 6, 8, 10, 12 единицам. Найти вероятность того, что с помощью взятых наугад трёх отрезков можно построить треугольник.
В группе a = 21 юноша и b = 18 девушек. Психолог для проведения однократного тестирования последовательно приглашает к себе трёх студентов (без возвращения). Найти вероятность
Группа студентов-спортсменов, состоящая из 6 студентов второго курса и 4 студентов третьего курса, проводит тренировку. Одновременно тренируются трое. Какова вероятность того, что тренируются студенты одного курса?
Комитет по качеству продуктов раз в месяц проверяет качество продуктов в двух из пятидесяти магазинов района. Какова вероятность того, что в течение месяца они оба будут проверены?

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Математика без Ху!ни. Теория вероятностей, комбинаторная вероятность.Скачать

Палку ломают случайным образом на 3 части.

Палку случайным образом ломают на три части; какова вероятность того, что из обломков можно составить треугольник? (Точки перелома равномерно распределены по длине палки)

Видео:Геометрическая вероятностьСкачать

Ответ

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Решение задачи

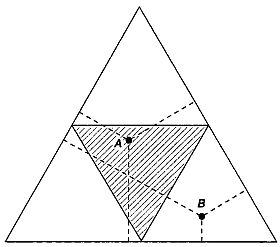
Действительно, нарисуем равносторонний треугольник и соединим середины его сторон отрезками прямых. У нас получится равносторонний треугольник меньших размеров, расположенный внутри первого (на рисунке меньший треугольник заштрихован). Сумма длин перпендикуляров, опущенных из любой точки большого треугольника на его стороны, не зависит от выбора точки и равна высоте большого треугольника. Если эту точку выбрать внутри меньшего треугольника (на рисунке этому условию удовлетворяет точка А), то любой из трех перпендикуляров будет не больше суммы двух других перпендикуляров. Следовательно, из отрезков, равных по длине трем перпендикулярам, опущенным из любой точки малого треугольника на стороны большого, всегда можно построить треугольник. Если же точка лежит вне малого треугольника (на рисунке — точка В), то один перпендикуляр заведомо длиннее суммы двух других перпендикуляров, и построить из таких перпендикуляров треугольник невозможно. Так как площадь заштрихованого треугольника составляет 1/4 площади всего треугольника, то искомая вероятность равна 1/4. Таким образом, если палку разломать на три части, то из ее обломков можно составить треугольник с вероятностью 1/4 (25%).

Видео:8 класс, 19 урок, Пропорциональные отрезкиСкачать

О задаче

Категория: Задачи на вероятность, Геометрические задачи,
Степень сложности: сложная.
Ключевые слова: 3, палка, треугольник,
Источник: Математические головоломки и развлечения,

Видео:Геометрическая вероятность. Видеоурок по алгебре 11 классСкачать

Скачать задачу

Вы можете скачать изображение с текстом задачи, поделиться им с друзьями в социальных сетях либо использовать в презентациях. Для скачивания, нажмите на картинке.

Видео:Задача, которую боятсяСкачать

Оставить комментарий

Свои вопросы, комментарии, замечания и занимательные задачи присылайте через предложенную ниже форму.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Решите задачу

Сколько лет твоему сыну? — спросил один человек своего приятеля. Приятель ответил: — Если к возрасту моего сына прибавить столько же да еще половину, то будет 10 лет. Сколько же лет сыну?

Видео:Геометрическая вероятностьСкачать