Отношение радиуса вписанной к радиусу описанной окружностей к треугольнику

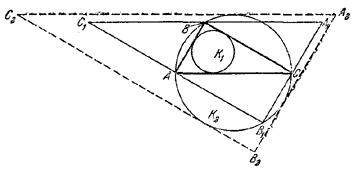
Проведем касательные к окружности K₂, параллельные сторонам (Delta)A₁B₁C₁, руководствуясь следующим правилом: касательная А₂В₂, параллельная стороне А₁В₁, касается K₂ в точке, лежащей на той же дуге (breve), на которой лежит вершина С и т. д. Отрезки проведенных касательных образуют (Delta)A₂B₂C₂.

Тогда (Delta)A₁B₁C₁лежит внутри (Delta)A₂B₂C₂и эти два треугольника подобны. Поэтому радиус R’ окружности, вписанной в (Delta)A₁B₁C₁, не больше радиуса R окружности K₂, вписанной в (Delta)A₂B₂C₂, т. е. R’ 2 = R 2 — 2Rr, доказанной в предыдущей задаче, следует, что R 2 — 2Rr > 0, откуда R > 2r.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Отношение радиуса вписанной к радиусу описанной окружностей к треугольнику

Основные метрические сооьтношения в прямоугольном треугольнике

§1. Прямоугольный треугольник. Метрические соотношения.

Основные метрические сооьтношения в прямоугольном треугольнике

Пусть `ABC` прямоугольный треугольник с прямым углом `C` и острым углом при вершине `A`, равным `alpha` (рис. 1).

Используем обычные обозначения:

`c` — гипотенуза `AB`;

`a` и `b` – катеты `BC` и `AC` (по-гречески «kathetos — катет» означает отвес, поэтому такое изображение прямоугольного треугольника нам представляется естественным);

`a_c` и `b_c` – проекции `BD` и `AD` катетов на гипотенузу;

`h` – высота `CD`, опущенная на гипотенузу;

`m_c` – медиана `CM`, проведённая к гипотенузе;

`R` – радиус описанной окружности;

`r` – радиус вписанной окружности.

Напомним, что если `alpha` — величина острого угла `A` прямоугольного треугольника `ABC` (см. рис. 1), то

`sin alpha = a/c`, `cos alpha = b/c` и `»tg»alpha = a/b`.

Значения синуса, косинуса и тангенса острого угла прямоугольного треугольника зависят только от меры угла и не зависят от размеров и расположения треугольника.

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:

`c^2 = a^2 + b^2`

Доказательство теоремы повторите по учебнику.

Выведем ряд соотношений между элементами прямоугольного треугольника.

Квадрат катета равен произведению гипотенузы и его проекции на гипотенузу

Если `/_ A = alpha` (см. рис. 1), то `/_ CBD = 90^@ — alpha` и `/_ BCD = alpha`. Из треугольника `ABC` `sin alpha = (BC)/(AB)`, а из треугольника `BCD` `sin alpha = (BD)/(BC)`.

Значит, `(BC)/(AB) = (BD)/(BC)`, откуда `BC^2 = AB * BD`, т. е. `a^2 = c * a_c` . Аналогично доказывается второе равенство.

Квадрат высоты, опущенной на гипотенузу, равен произведению проекции катетов на гипотенузу

Из треугольника `ACD` (рис. 1) имеем `»tg»alpha = (CD)/(AD)`, а из треугольника `BCD` `»tg»alpha = (BD)/(CD)`.

Значит `(BD)/(CD) = (CD)/(AD)`, откуда `CD^2 = AD * BD`, т. е. `h^2 = a_c * b_c`.

Произведение катетов равно произведению гипотенузы и высоты, опущенной на гипотенузу

Из треугольника `ABC` имеем `sin alpha = (BC)/(AB)`, а из треуольника `ACD` `sin alpha = (CD)/(AC)`.

Таким образом, `(BC)/(AB) = (CD)/(AC)`, откуда `BC * AC = AB * CD`, т. е. `a * b = c * h`.

Медиана, проведённая к гипотенузе, равна половине гипотенузы, т. е.

Пусть `AM = BM`. Проведём $$ MKVert BC$$ (рис. 2), тогда по теореме Фалеса `AK = CK`

.

Кроме того, из того, что `BC _|_ AC` и $$ MKVert BC$$ следует `MK _|_ AC`. В прямоугольных треугольниках `CMK` и `AMK` катет `MK` общий, катеты `CK` и `AK` равны. Эти треугольники равны и `CM = AM`, т. е. `CM = 1/2 AB`.

Полезно также запомнить, что медиана к гипотенузе разбивает треугольник на два равнобедренных треугольника.

Радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы

Это следует из Свойства 4, действительно, `MA = MB = MC`, следовательно, окружность с центром в точке `M` и радиуса `c/2` проходит через три вершины.

Сумма катетов равна удвоенной сумме радиусов описанной и вписанной окружностей

`a + b = 2(R + r)` или `a + b = c + 2r`

Пусть `O` — центр вписанной окружности и `F`, `N` и `S` — точки касания сторон треугольника `ABC` (рис. 3), тогда `OF_|_ BC`, `ON _|_ AC`, `OS _|_ AB` и `OF = ON = OS = r`. Далее, `OFCN` — квадрат со стороной `r`, поэтому `BF = BC — FC`, `AN = AC — CN`, т. е. `BF = a — r` и `AN = b — r`.

Прямоугольные треугольники `AON` и `AOS` равны (гипотенуза `AO` — общая, катеты `ON` и `OS` равны), следовательно, `AS = AN`, т. е. `AS = b — r`.

Аналогично доказывается, что `BS = a — r`, поэтому из `AB = AS + BS` следует `c = (b — r) + (a — r)`, т. е. `a + b = c + 2r`. Зная, что `c = 2R`, окончательно получаем `a + b = 2(R + r)`.

Равенства, доказанные в Свойствах 1 и 2, записываются также как:

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Треугольник вписанный в окружность

Видео:Радиус описанной окружностиСкачать

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

1. Радиус вписанной окружности в треугольник,
   если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

1. Радиус описанной окружности около треугольника,
   если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

1. Площадь треугольника вписанного в окружность,
   если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = fracab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

1. Периметр треугольника вписанного в окружность,
   если известны все стороны:
   

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

1. Сторона треугольника вписанного в окружность,
   если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

1. Средняя линия треугольника вписанного
   в окружность, если известно основание:
   

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

1. Высота треугольника вписанного в окружность,
   если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Свойства

• Центр вписанной в треугольник окружности
  находится на пересечении биссектрис.
• В треугольник, вписанный в окружность,
  можно вписать окружность, причем только одну.
• Для треугольника, вписанного в окружность,
  справедлива Теорема Синусов, Теорема Косинусов
  и Теорема Пифагора.
• Центр описанной около треугольника окружности
  находится на пересечении серединных перпендикуляров.
• Все вершины треугольника, вписанного
  в окружность, лежат на окружности.
• Сумма всех углов треугольника — 180 градусов.
• Площадь треугольника вокруг которого описана окружность, и
  треугольника, в который вписана окружность, можно найти по
  формуле Герона.

Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

1. Проведем серединные
   перпендикуляры — HO, FO, EO.
2. O — точка пересечения серединных
   перпендикуляров равноудалена от
   всех вершин треугольника.
3. Центр окружности — точка пересечения
   серединных перпендикуляров — около
   треугольника описана окружность — O,
   от центра окружности к вершинам можно
   провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

🔍 Видео

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

найти радиус окружности, описанной вокруг треугольникаСкачать

Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Геометрия. 9 класс. Формулы для нахождения радиусов вписанной и описанной окружностей треугольникаСкачать

Пара фактов про окружность | Ботай со мной #067 | Борис Трушин |Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать

ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТЬ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Построить описанную окружность (Задача 1)Скачать

№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать

Формулы радиусов описанной и вписанной окружностей правильного многоугольника 2Скачать

9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать