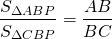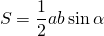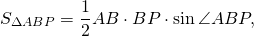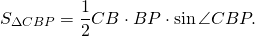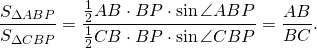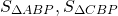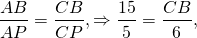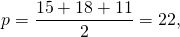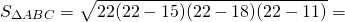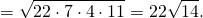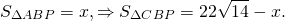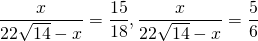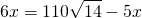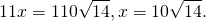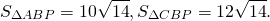Биссектриса делит площадь треугольника пропорционально прилежащим сторонам.

Площадь треугольника равна половине произведения сторон на синус угла между ними
Так как BP — биссектриса треугольника ABC, то ∠ABP=∠CBP, отсуда sin∠ABP=sin∠CBP.
Что и требовалось доказать .
Биссектриса треугольника делит противоположную сторону на части 5 и 6. Меньшая из двух других сторон равна 15. Найти площади частей, на которые биссектриса делит исходный треугольник.

BP — биссектриса, AP=5, CP=6, AB=15
откуда BC=18. AC=AP+CP=11.
Площадь треугольника ABC найдём по формуле Герона.
Так как биссектриса делит площадь треугольника на части, пропорциональные прилежащим сторонам,
Ответ: 10√14 и 12√14.
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

3 Comments
Биссектриса угла треугольника делит его сторону наотрезки, разность которых 3см, две другие стороны 14см и 21см. Вычислить площадь треугольника.
Пусть один из отрезков равен x см, тогда другой — (x+3) см. По свойству биссектрисы треугольника 14:21=x:(x+3). Отсюда x=6, x+3=9, то есть длина третьей стороны треугольника 6+9=15 см. Зная все три стороны треугольника, площадь можем найти по формуле Герона.
Видео:8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать

Основные свойства площадей треугольников
Факт 1.
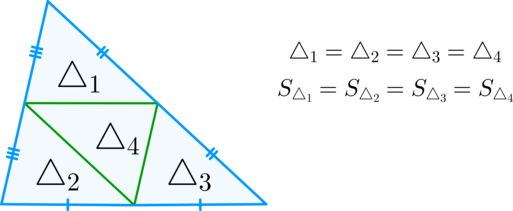
(bullet) Средние линии треугольника разбивают его на 4 равных треугольника.
Соответственно, площади этих треугольников равны.
Факт 2.
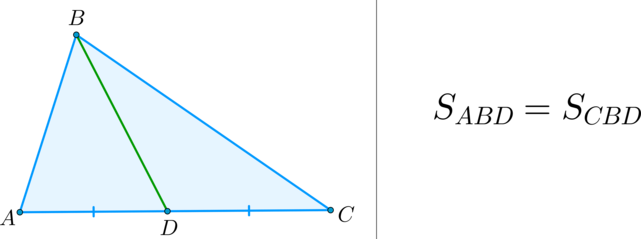
(bullet) Медиана треугольника делит его на два треугольника, равных по площади (равновеликих).
Факт 3.
(bullet) Все 3 медианы треугольника делят его на 6 равновеликих треугольников.
Факт 4.
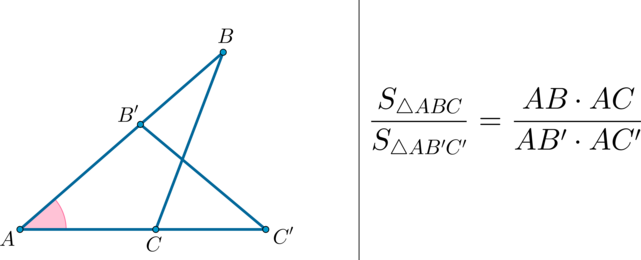
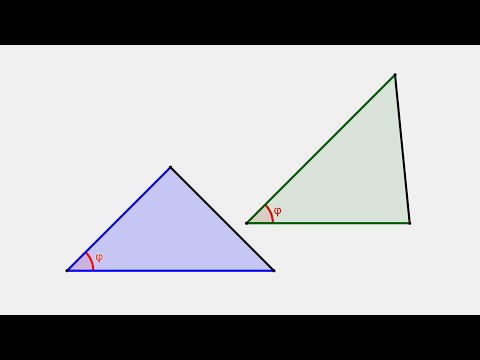
(bullet) Площади треугольников, имеющих одинаковый угол, относятся как произведения сторон, образующих этот угол.
Факт 5.
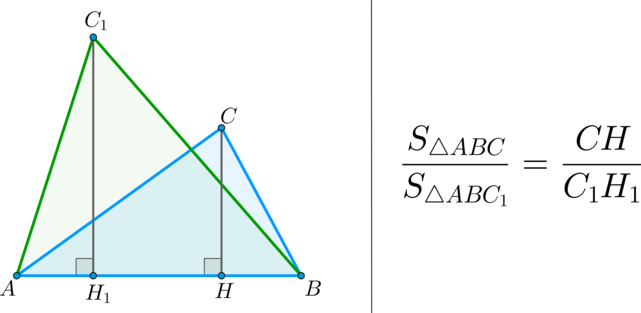
(bullet) Площади треугольников, имеющих одинаковое основание, относятся как высоты, проведенные к этим основаниям.
Факт 6.
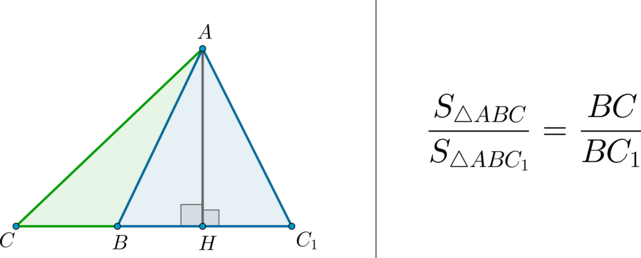
(bullet) Площади треугольников, имеющих одинаковую высоту, относятся как основания, к которым проведена эта высота.
Факт 7.
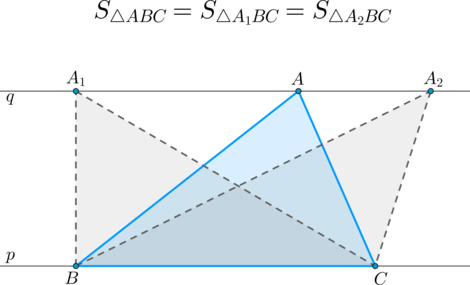
(bullet) Если прямые (p) и (q) параллельны, то
Факт 8.
(bullet) Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
(bullet) Отношение периметров подобных треугольников равно коэффициенту подобия.
Видео:Отношение площадей треугольников с равным угломСкачать
Определение и свойства биссектрисы угла треугольника
В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.
Видео:Геометрия 8 класс (Урок№14 - Определение подобных треугольников. Отношение площадей подобных фигур.)Скачать

Определение биссектрисы угла треугольника
Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.
Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.
Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.
Внешней называется биссектриса угла, смежного с внутренним углом треугольника.
Видео:Секретные формулы биссектрисы треугольника!😉❤️🔥#математика #егэСкачать

Свойства биссектрисы треугольника
Свойство 1 (теорема о биссектрисе)
Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):
Свойство 2
Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.
Свойство 3
Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).
Свойство 4
Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):
BD 2 = AB ⋅ BC – AD ⋅ DC
Свойство 5
Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.
- CD – внутренняя биссектриса ∠ACB;
- CE – биссектриса угла, смежного с ∠ACB;
- ∠DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.
Видео:Задание 26 Отношение площадей Свойство биссектрисыСкачать

Пример задачи
Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.
Решение
Нарисуем чертеж согласно условиям задачи.
Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.
Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):
Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29
Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.
Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.
📺 Видео
Задача по геометрии № 25 ОГЭ на отношение площадейСкачать

Геометрия 8 класс : Отношение площадей подобных треугольниковСкачать

#57. Отношение площадей треугольников — самые надежные отношения!Скачать

Короткие загадки, которые осилит не каждый профессорСкачать

8 класс, 22 урок, Первый признак подобия треугольниковСкачать

3 свойства биссектрисы #shortsСкачать

Свойство биссектрисы треугольника с доказательствомСкачать

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

ПОСТРОЕНИЕ БИССЕКТРИСЫ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Свойство биссектрисы внешнего угла треугольникаСкачать

Задание 26 Отношение площадей Свойство биссектрисыСкачать

Площади треугольников с равным углом.Скачать

Высота, биссектриса, медиана. 7 класс.Скачать

Свойства биссектрисыСкачать