Около окружности радиуса 5 вписана равнобедренная трапеция

Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .

Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .

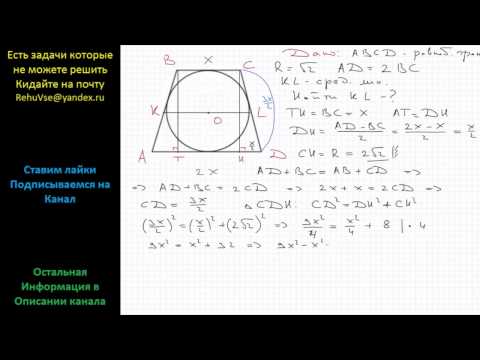
Видео:Геометрия В равнобедренную трапецию вписана окружность радиуса R. Верхнее основание трапеции в 2Скачать

Свойства трапеции

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.

Коэффициент подобия –

Отношение площадей этих треугольников есть .

4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.

5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.

7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

Видео:Геометрия Около окружности радиуса √2 описана равнобедренная трапеция, у которой одно основаниеСкачать

Свойства и признаки равнобедренной трапеции

1. В равнобедренной трапеции углы при любом основании равны.

2. В равнобедренной трапеции длины диагоналей равны.

3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.

4. Около равнобедренной трапеции можно описать окружность.

5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Видео:Задача про трапецию, описанную около окружностиСкачать

Вписанная окружность

Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то

Видео:Задача 6 №27926 ЕГЭ по математике. Урок 141Скачать

Площадь

или где – средняя линия

Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Видео:Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Равнобедренная трапеция описано около окружности радиуса 3√5 . Найдите тангенс угла при большем основании трапеции, если её средняя линия равна 15

Видео:Около трапеции описана окружностьСкачать

Ваш ответ

Видео:Радиус описанной окружности трапецииСкачать

решение вопроса

Видео:🔴 На окружности радиуса 5 отмечена точка C ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

Похожие вопросы

• Все категории
• экономические 43,280
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,971
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Основания равнобедренной трапеции равны 72 и 30. Центр окружности, описанной около трапеции... (ЕГЭ)Скачать

Материалы для подготовки к ГИА «Задачи по теме «Трапеция и ее свойства »

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

МУНИЦИПАЛЬНОЕ АВТОНОМНОЕ

СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 96

Готовимся к ГИА

Задачи по теме «Трапеция и ее свойства »

Автор: Кошелева Е.В.,

Решите задачи, используя следующие свойства

1)Высота равнобедренной трапеции, в которую можно вписать окружность, является средним геометрическим её оснований h 2 = a ∙ b

В равнобедренную трапецию вписана окружность радиуса 10 . Верхнее основание трапеции в два раза меньше её высоты. Найдите площадь трапеции.

Около круга радиуса 2 описана равнобедренная трапеция, периметр которой равен 20. Найти площадь этой трапеции.

Основания описанной около окружности равнобедренной трапеции равны 2 и 18. Найдите площадь трапеции.

Основания равнобедренной трапеции относятся как 1 : 5, а радиус окружности, вписанной в эту трапецию, равен 7,5 см. Найдите стороны трапеции

Ответ:

Около окружности с диаметром 15 описана равнобедренная трапеция с боковой стороной, равной 17. Найдите основания трапеции.

В равнобокую трапецию с верхним основанием, равным 1, вписана окружность единичного радиуса. Найти нижнее основание трапеции.

В равнобокую трапецию вписана окружность радиуса 6 см, точка касания делит боковую сторону на отрезки, разность между которыми равна 5 см. Найти среднюю линию трапеции.

Средняя линия равнобедренной трапеции равна 5 см. Известно, что средняя линия делит площадь трапеции на две части, площади которых относятся как 7:13. Найти высоту трапеции, если известно, что в неё можно вписать окружность.

В равнобедреннуютрапецию вписан круг. Боковая сторона делится точкой касания на отрезки длиной 9 и 16. Определить площадь трапеции .

Около окружности, радиус которой равен 10, описана равнобедренная трапеция. Расстояния между точками касания окружности с боковыми сторонами трапеции12. Найдите боковую сторону трапеции.

Ответ:

Средняя линия равнобокой трапеции, описанной около круга, равна 68. Найти радиус этого круга, если нижнее основание трапеции больше верхнего на 64.

В равнобедренную трапецию, большее основание которой равно 36, вписана окружность радиуса 12. Найдите наименьшее основание трапеции

2 ) Если в равнобедренную трапецию вписана окружность, то её боковая сторона равна средней линии

1.Около круга радиуса 2 см описана равнобедренная тра пеция с острым углом 30°. Найти длину средней линии трапеции. Ответ: 8

Найти боковую сторону равнобокой трапеции, описанной около круга, если острый угол при основании трапеции равен , а площадь трапеции 288.

Около окружности описана равнобедренная трапеция, средняя линия которой равна 5, а синус острого угла при основании равен 0,8. Найдите площадь трапеции.

Около окружности описана трапеция, площадь которой равна 20, а синусы углов при основании равны 0,8. Найти длину средней линии трапеции.

Равнобедренная трапеция описана около окружности радиуса 5. Боковая сторона равна 12. Чему равна площадь трапеции?

Равнобокая трапеция с площадью 40 и боковым ребром 8 такова, что в неё можно вписать окружность. Найти радиус окружности.

Площадь равнобедренной трапеции, описанной около окружности, равна 8 . Найдите среднюю линию трапеции, если острый угол при её основании равен 30°.

В равнобедренную трапецию вписана окружность радиуса 4. Боковая сторона равна 9. Найти площадь трапеции.

В равнобедренной трапеции боковая сторона равна средней линии, а периметр равен 48. Найдите длину боковой стороны.

В равнобедренную трапецию, один из углов которой равен 60°, а площадь равна , вписана окружность. Найдите радиус этой окружности.

3)Площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна квадрату её высоты: S = h 2 .

Диагонали равнобедренной трапеции взаимно перпендикулярны, а длина её средней линии равна 9. Найдите длину отрезка, соединяющего середины оснований трапеции.

В равнобедренной трапеции средняя линия равна 5 , а диагонали взаимно перпендикулярны. Найдите площадь этой трапеции

Найти площадь равнобедренной трапеции, основания которой 12 и 34, а диагонали перпендикулярны

В равнобедреннойтрапеции диагонали взаимно перпендикулярны. Найдите среднюю линию трапеции , если её площадь равна 36.

Диагонали равнобедренной трапеции взаимно перпендикулярны, а её площадь равна 4. Найти высоту трапеции.

Найти периметр равнобедренной трапеции, боковая сторона которой 13, высота 12, а диагонали взаимно перпендикулярны.

Площадь равнобедренной трапеции равна 256, а диагонали взаимно перпендикулярны. Найдите среднюю линию трапеции.

В равнобедренной трапеции ABCD (BC || AD) диагонали AC и BD взаимно перпендикулярны, ВС = 6 см, AD = 20 см. Найти длину отрезка, соединяющего середины оснований трапеции.

В равнобедренной трапеции ABCD ( AD || BC ) Диагонали взаимно перпендикулярны, высота трапеции равна 12 см. Расстояние от вершины А до прямой CD в три раза больше, чем расстояние от вершины В до этой прямой. Найдите основания трапеции.

Ответ: 18 см и 6см

4)В равнобедренной трапеции проекция диагонали на большее основание равна средней линии трапеции.

Найти диагональ равнобедренной трапеции, если её площадь равна , а средняя линия равна 2

Найти площадь равнобедренной трапеции, если её высота равна 4, а тангенс угла между диагональю и основанием равен .

Найти площадь равнобедренной трапеции, если её диагональ, равная 13, образует с основанием угол, косинус которого равен .

Большее основание равнобедренной трапеции равно 8, боковая сторона 9, а диагональ 11. Найти меньшее основание.

Меньшее основание равнобедренной трапеции равно 10, боковая сторона 18, а диагональ 22. Найти большее основание трапеции.

Найдите площадь равнобедренной трапеции, если её средняя линия равна 6, а тангенс угла между диагональю и основанием равен 1,5.

Найдите площадь равнобедренной трапеции, если её диагональ равна , а средняя линия равна

Средняя линия равнобедренной трапеции равна 4. Площадь трапеции равна 8. Найти тангенс угла между диагональю и основанием трапеции

В равнобедренной трапеции диагональ, равная 4 см, составляет с основанием угол 60°. Найдите среднюю линию трапеции.

Боковая сторона равнобедренной трапеции равна , а основания равны 4 и 5. Найдите её диагональ

В равнобокой трапеции основания 6 и 10. Диагональ равна 10. Найти площадь трапеции

Площадь равнобедренной трапеции равна 32. Котангенс угла между диагоналями трапеции и её основанием равен 2. Найдите высоту трапеции.

В равнобедренной трапеции диагональ равна 13 см, а средняя линия – 12 см. Найдите высоту трапеции

📽️ Видео

Окружность вписана в равнобедренную трапецию. Теорема в задаче. Геометрия, ОГЭ, ЕГЭ. Высота и радиусСкачать

Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Задача.Скачать

Задание 26_Равнобедренная трапеция. Вписанная окружность.Скачать

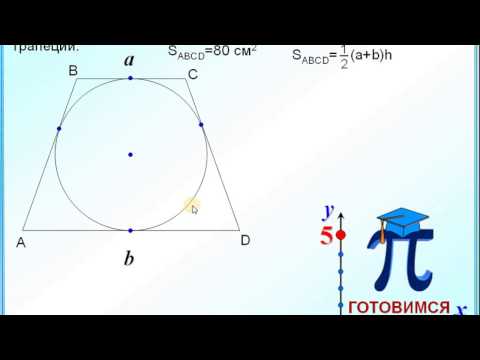
Боковые стороны трапеции, описанной около окружности, равны 13 и 1. Найдите среднюю линию трапеции.Скачать

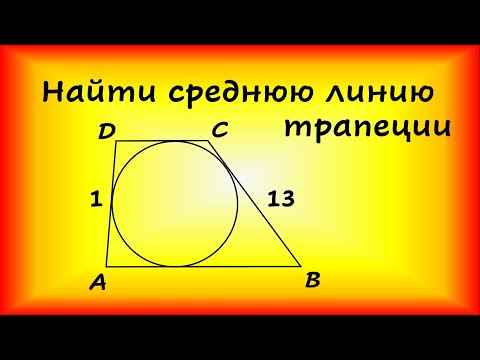
Почему любая вписанная трапеция будет равнобедренной? #геометрияегэСкачать

Всегда ли трапеция вписанная в окружность РАВНОБЕДРЕННАЯ? Задача. ЕГЭ, ОГЭ.Скачать

В равнобедренную трапецию вписана окружность, средняя линия трапеции 3, диагональ 5. Найти высоту трСкачать

Трапеция, вписанная в окружностьСкачать

Задание из ЕГЭ: трапеция в окружности #геометрия #егэ2023 #трапеция #окружностьСкачать