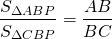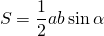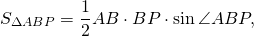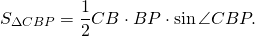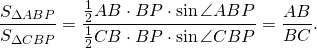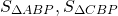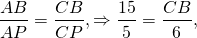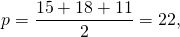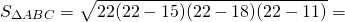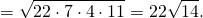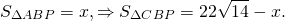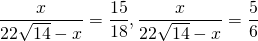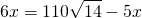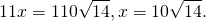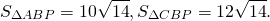Отношение площадей треугольников биссектрисы (5 видео)

Биссектриса делит площадь

Биссектриса делит площадь треугольника пропорционально прилежащим сторонам.

Дано : ∆ABC,

Площадь треугольника равна половине произведения сторон на синус угла между ними

Так как BP — биссектриса треугольника ABC, то ∠ABP=∠CBP, отсуда sin∠ABP=sin∠CBP.

Что и требовалось доказать .

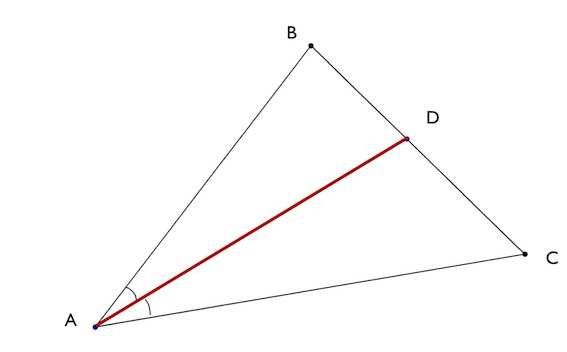
Биссектриса треугольника делит противоположную сторону на части 5 и 6. Меньшая из двух других сторон равна 15. Найти площади частей, на которые биссектриса делит исходный треугольник.

Дано : ∆ABC,

BP — биссектриса, AP=5, CP=6, AB=15

откуда BC=18. AC=AP+CP=11.

Площадь треугольника ABC найдём по формуле Герона.

Так как биссектриса делит площадь треугольника на части, пропорциональные прилежащим сторонам,

Ответ: 10√14 и 12√14.

Содержание

3 Comments
Отношение площадей треугольников биссектрисы
Элементы треугольника. Биссектриса
Свойства биссектрисы
Некоторые формулы, связанные с биссектрисой треугольника
📽️ Видео

Видео:Задание 26 Отношение площадей Свойство биссектрисыСкачать

3 Comments

Биссектриса угла треугольника делит его сторону наотрезки, разность которых 3см, две другие стороны 14см и 21см. Вычислить площадь треугольника.

Пусть один из отрезков равен x см, тогда другой — (x+3) см. По свойству биссектрисы треугольника 14:21=x:(x+3). Отсюда x=6, x+3=9, то есть длина третьей стороны треугольника 6+9=15 см. Зная все три стороны треугольника, площадь можем найти по формуле Герона.

Видео:Задача по геометрии № 25 ОГЭ на отношение площадейСкачать

Отношение площадей треугольников биссектрисы

Две фигуры $$ F$$ и $$ ^<text>$$ называются подобными, если они переводятся друг в друга преобразованием подобия, т. е. таким преобразованием, при котором расстояния между двумя точками изменяются (увеличиваются или уменьшаются) в одно и то же число раз. Если фигуры $$ F$$ и $$ ^<text>$$ подобны, то пишется $$ Fsim ^<text>$$Напомним, что в записи подобия треугольников $$ ∆ABC

Два треугольника подобны:

1) если два угла одного соответственно равны двум углам другого;
2) если две стороны одного пропорциональны двум сторонам другого и углы, образованные этими сторонами, равны;
3) если три стороны одного треугольника пропорциональны трём сторонам другого.

Из признаков подобия следует утверждения, которые удобно использовать в решении задач:

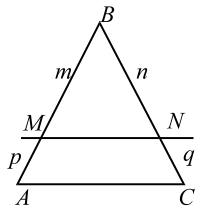
1°. Прямая, параллельная одной из сторон треугольника и пересекающая две другие в различных точках, отсекает треугольник, подобный данному.

Отношение площадей треугольников биссектрисы

Рис. 5

2°. Прямая, параллельная одной из сторон треугольника и пересекающая две другие стороны, отсекает на них отрезки, пропорциональные данным сторонам, т. е. если $$ MNleft|right|AC$$ (рис. 5), то

3°. Если прямая пересекает две стороны треугольника и отсекает на них пропорциональные отрезки, то она параллельна третьей стороне, т. е. если (см. рис. 5)

то $$ MN$$ параллельна $$ AC$$ (доказательство было дано в задании для 9 класса).

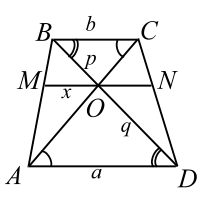
Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках $$ M$$ и $$ N$$. Найти длину отрезка `MN`, если основания трапеции равны $$ a$$ и $$ b$$.

Пусть $$ O$$ точка пересечения диагоналей трапеции (рис. 6). Обозначим:

$$ AD=a, BC=b, MO=x, BO=p, OD=q.$$

$$1.;left.beginBCparallel AD\bigtriangleup BOCsimbigtriangleup DOA;(mathrm;mathrm;mathrm)endright|Rightarrowdfrac ba=dfrac pq$$ (1)

$$2.;left.beginMOparallel AD\bigtriangleup MBOsimbigtriangleup ABDendright|Rightarrowdfrac xa=dfrac p

$$. (2)

Результат этой задачи, как утверждение, верное для любой трапеции, следует запомнить.

Рис. 6

Из определения подобия фигур следует, что в подобных фигурах все соответствующие линейные элементы пропорциональны. Так, отношение периметров подобных треугольников равно отношению длин соответствующих сторон. Или, например, в подобных треугольниках отношение радиусов вписанных окружностей (также и описанных окружностей) равно отношению длин соответствующих сторон. Это замечание поможет нам решить следующую задачу.

Рис. 7

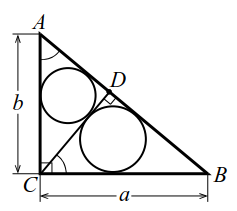
В прямоугольном треугольнике $$ ABC$$ из вершины $$ C$$ прямого угла проведена высота $$ CD$$ (рис. 7). Радиусы окружностей, вписанных в треугольники $$ ACD$$ и $$ BCD$$ равны соответственно $$ _$$ и $$ _$$. Найти радиус окружности, вписанной в треугольник $$ ABC$$.

Напомним, что площади подобных фигур относятся как квадраты соответствующих линейных элементов. Для треугольников это утверждение можно сформулировать так: площади подобных треугольников относятся как квадраты соответствующих сторон. Рассмотрим характерную задачу на эту тему.

Рис. 8

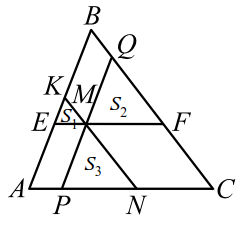
Через точку $$ M$$, лежащую внутри треугольника $$ ABC$$, проведены три прямые, параллельные его сторонам. При этом образовались три треугольника (рис. 8), площади которых равны $$ ~~_$$, $$ ~~_$$ и $$ ~~_$$. Найти площадь треугольника $$ ABC$$.~~~~~~

~~Легко видеть, что треугольники $$ EKM$$, $$ MQF$$ и $$ PMN$$ подобны треугольнику $$ ABC$$.~~

~~Пусть $$ S$$ -площадь треугольника $$ ABC$$, тогда~~

~~А так как $$ EM=AP, MF=NC$$, то $$ EM+PN+MF=AP+PN+NC=AC$$.~~

~~Свойства медиан, высот, биссектрис треугольника~~

В наших заданиях 9-го и 10-го классов здесь повторяемые теоремы и утверждения были доказаны. Для некоторых из них мы напоминаем пути доказательств, доказывая их моменты и давая поясняющие рисунки.

Рис. 9

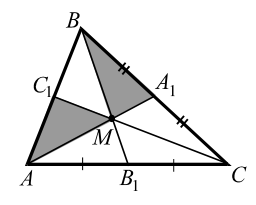
Теорема 1. Три медианы треугольника пересекаются в одной точке и точкой пересечения каждая медиана делится в отношении `2 : 1`, считая от вершины.

Теорема 2. Три медианы, пересекаясь, разбивают треугольник на `6` треугольников с общей вершиной, площади которых равны между собой.

(На рис. 9 площадь каждого из `6` треугольников с вершиной `M` и основанием, равным половине стороны, равна $$ <displaystyle frac>_$$. Точка пересечения медиан называется центром тяжести треугольника.

~~Теорема 3. Пусть $$ BD$$ — медиана треугольника~~

Рис. 10

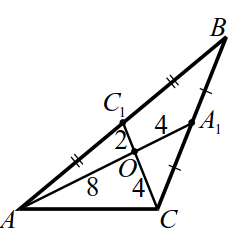
Расставим на рисунке 10 длины отрезков медиан. По условию, одна из сторон треугольника равна `12`, сторона $$ AC$$ не может равняться `12`, иначе $$ AC=AO+OC$$ — нарушено неравенство треугольника. Также не может равняться `12` сторона $$ AB$$, так в этом случае $$ A_=6$$ и треугольник $$ AO_$$ со сторонами `8`, `2`, `6` не существует. Значит, $$ BC=12$$ и $$ A_=6$$.

~~2. Площадь треугольника находим по формуле Герона:~~

~~По теореме 2 площадь треугольника $$ ABC$$ в `6` раз больше, находим $$ ~~_=18sqrt$$.~~~~

Теорема 4. Три высоты треугольника или три прямые, на которых лежат высоты, пересекаются в одной точке. (Эта точка называется ортоцентром треугольника). В остроугольном треугольнике точка пересечения высот лежит внутри треугольника.

~~Были доказаны также две леммы о высотах~~

~~1-ая лемма.~~


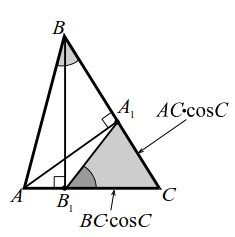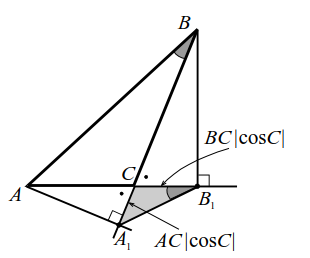Рис. 11a	Рис. 11б

~~2-ая лемма.~~


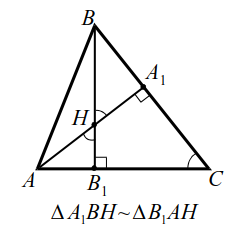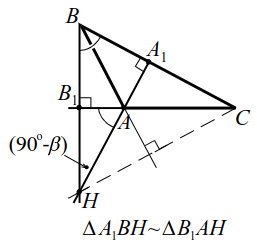Рис. 12a	Рис. 12б

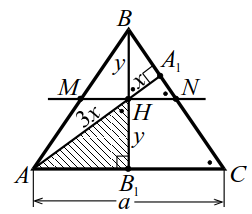Рис. 13

1. Точка $$ H$$ — середина высоты (рис. 13). Если отрезок $$ MH$$ проходит через точку $$ H$$ и параллелен основаниям, то `MN` — средняя линия; `MN=a/2`.

3. $$ angle _BC=90°-angle C$$, поэтому `ul(/_BHA_1=/_AHB_1=/_C)`, а по второй лемме о высотах $$ AH·H_=BH·H_$$ т. е. $$ 3^=^, y=xsqrt$$.

Теорема 5. Биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам, т. е. если $$ AD$$ — биссектриса треугольника $$ ABC$$ (рис. 14), то

~~Доказательство легко выполните сами, применяя теорему синусов к треугольникам $$ ADB$$ и $$ ADC$$.~~

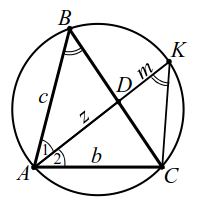
Теорема 6. Пусть $$ AD$$ — биссектриса треугольника $$ ABC$$ (рис. 14), тогда $$ AD=sqrt$$ (в обозначениях рисунка 14а)


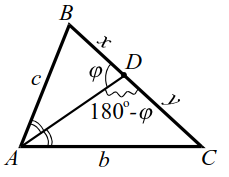Рис. 14	Рис. 14а

Эту теорему докажем. Опишем около треугольника $$ ABC$$ окружность, точку пересечения прямой $$ AD$$ и окружности обозначим $$ K$$ (рис. 14а).

~~По свойству пересекающихся хорд: $$ AD·DK=BD·CD$$, т. е. $$ z·m=x·y$$, тогда $$ ^=bc-xy$$, $$ z=sqrt$$.~~

В треугольнике $$ ABC$$ со сторонами $$ AB=5$$, $$ AC=3$$ биссектриса $$ AD=<displaystyle frac>$$. Найти сторону $$ BC$$ и радиус вписанной окружности.

~~Видео:8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать~~

Элементы треугольника. Биссектриса

Биссектриса треугольника – отрезок биссектрисы угла треугольника, заключенный между вершиной треугольника и противолежащей ей стороной.

~~Видео:Задание 26 Отношение площадей Свойство биссектрисыСкачать~~

Свойства биссектрисы

~~1. Биссектриса треугольника делит угол пополам.~~

2. Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон ()

~~3. Точки биссектрисы угла треугольника равноудалены от сторон этого угла.~~

4. Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности.

~~Видео:Свойство биссектрисы треугольника с доказательствомСкачать~~

Некоторые формулы, связанные с биссектрисой треугольника

(доказательство формулы – здесь)
, где
— длина биссектрисы, проведённой к стороне ,
— стороны треугольника против вершин соответственно,
— длины отрезков, на которые биссектриса делит сторону ,

Приглашаю посмотреть видеоурок, в котором демонстрируется применение всех указанных выше свойств биссектрисы.

Задачи, рассматриваемые в видеоролике:
1.В треугольнике АВС со сторонами АВ=2 см, ВС=3 см, АС=3 см проведена биссектриса ВМ. Найти длины отрезков АМ и МС
2. Биссектриса внутреннего угла при вершине А и биссектриса внешнего угла при вершине С треугольника АВС пересекаются в точке М. Найдите угол BMC, если угол В равен 40, угол С – 80 градусов
3. Найти радиус окружности, вписанной в треугольник, считая стороны квадратных клеток равными 1