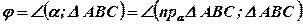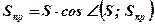Ортогональное проецирование:
Параллельное проецирование, направление которого перпендикулярно плоскости проекции, называется ортогональным проецированием. Проекция фигуры, образующаяся при ортогональном проецировании, называется ортогональной проекцией, или просто проекцией этой фигуры.
Поскольку ортогональное проецирование является особым видом параллельного проецирования, то для него выполняются все свойства последнего. Ортогональной проекцией прямой
Отметим, что прямые, перпендикулярные одной из параллельных плоскостей, перпендикулярны и остальным, поэтому ортогональное проецирование на одну из таких плоскостей будет ортогональным и на остальные плоскости. Очевидно, что ортогональные проекции фигуры на параллельные плоскости равны между собой.
Ортогональное проецирование также имеет только ему присущие свойства. Одно из них выражает теорема о площади ортогональной проекции многоугольника.
Площадь ортогональной проекции
Теорема 5
Площадь ортогональной проекции произвольного многоугольника на плоскость равна произведению площади самого многоугольника на косинус угла между плоскостью многоугольника и плоскостью проекции.
Как пример многоугольника возьмем 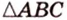
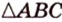
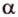
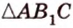
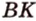
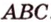
о трех перпендикулярах 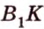
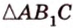
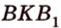
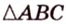
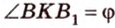
Учитывая, что 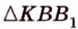
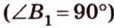
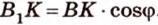
Итак, 
Чтобы доказать теорему для произвольного многоугольника, его разбивают на треугольники. Тогда для каждого треугольника и его проекции можно записать равенство
где 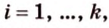
Получим в левой части равенства площадь проекции многоугольника, а в правой — площадь самого многоугольника, умноженную на косинус угла между их плоскостями. Отсюда
Т.е. и для этого случая теорема истинна.
Пример:
Ортогональной проекцией треугольника является треугольник со сторонами 13 см, 14 см и 15 см. Плоскость треугольника образует с плоскостью проекции угол 60°. Вычислите площадь данного треугольника.
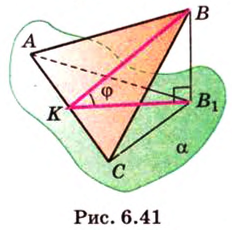
Воспользуемся рисунком 6.41. Известно, что площадь проекции треугольника вычисляют по формуле:
где 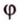
По формуле Герона найдем площадь 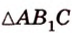
где 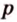
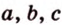
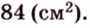
Тогда
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Декартовы координаты на плоскости
- Декартовы координаты в пространстве
- Геометрические преобразования в геометрии
- Планиметрия — формулы, определение и вычисление
- Параллельность прямых и плоскостей
- Перпендикулярность прямой и плоскости
- Взаимное расположение прямых в пространстве, прямой и плоскости
- Перпендикулярность прямых и плоскостей в пространстве
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать

Проекция многоугольника на плоскость
Площадь проекции многоугольника
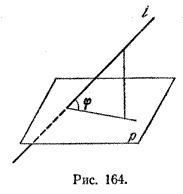
Напомним, что углом между прямой и плоскостью называется угол между данной прямой и ее проекцией на плоскость (рис. 164).
Теорема. Площадь ортогональной проекции многоугольника на плоскость равна площади проектируемого многоугольника, умноженной на косинус угла, образованного плоскостью многоугольника и плоскостью проекции.
Каждый многоугольник можно разбить на треугольники, сумма площадей которых равна площади многоугольника. Поэтому теорему достаточно доказать для треугольника.
Пусть (Delta)АВС проектируется на плоскость р. Рассмотрим два случая:
а) одна из сторон (Delta)АВС параллельна плоскости р;
б) ни одна из сторон (Delta)АВС не параллельна р.
Рассмотрим первый случай: пусть [АВ] || р.
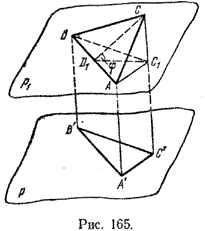
Проведем через (АВ) плоскость р1 || р и спроектируем ортогонально (Delta)АВС на р1 и на р (рис. 165); получим (Delta)АВС1 и (Delta)А’В’С’.
По свойству проекции имеем (Delta)АВС1 (cong) (Delta) А’В’С’, и поэтому
Проведем [CD1] ⊥ [AB] и отрезок D1C1. Тогда [D1C1] ⊥ [AB], a (widehat<CD_C_>) = φ есть величина угла между плоскостью (Delta) АВС и плоскостью р1. Поэтому
и, следовательно, S(Delta)A’B’C’ = S(Delta)ABC cos φ.
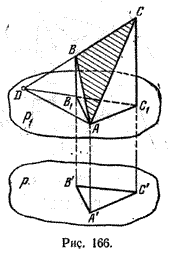
Перейдем к рассмотрению второго случая. Проведем плоскость р1 || р через ту вершину (Delta)АВС, расстояние от которой до плоскости р наименьшее (пусть это будет вершина А).
Спроектируем (Delta)АВС на плоскости р1 и р (рис. 166); пусть его проекциями будут соответственно (Delta)АВ1С1 и (Delta)А’В’С’.
Пусть (ВС) ( cap ) p1 = D. Тогда
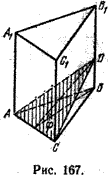
Задача. Через сторону основания правильной треугольной призмы проведена плоскость под углом φ = 30° к плоскости ее основания. Найти площадь образующегося сечения, если сторона основания призмы а = 6 см.
Изобразим сечение данной призмы (рис. 167). Так как призма правильная, то ее боковые ребра перпендикулярны плоскости основания. Значит, (Delta)АВС есть проекция (Delta)АDС, поэтому
$$ S_ = frac<S_> = frac $$
или
$$ S_ = frac<4cdotfrac> = 18 (см^2) $$
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

ОРТОГОНАЛЬНАЯ ПРОЕКЦИЯ И ЕЁ СВОЙСТВА

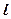
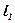
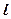

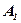
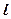
p — плоскость проекции;
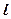



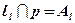
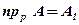
Ортогональное проектирование является частным случаем параллельного проектирования. Ортогональное проектирование — это такое параллельное проектирование, при котором прямая проектирования перпендикулярна плоскости проекции.Ортогональное проектирование широко применяется в техническом черчении, где фигура проектируется на три плоскости — горизонтальную и две вертикальные.

Обозначение: 


Определение: Ортогональной проекцией фигуры F на плоскость p называется множество всех точек плоскости, являющихся ортогональными проекциями множества точек фигуры F на плоскость p.
Ортогональное проектирование, как частный случай параллельного проектирования, обладает теми же свойствами:
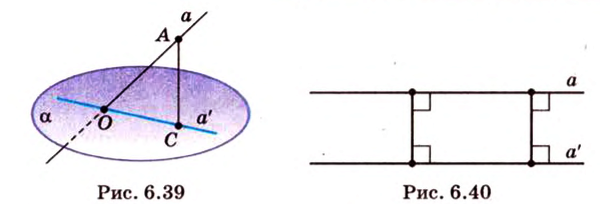
При проектировании точка пространства отображается в точку плоскости проекции.
- Каждая точка плоскости проекции отображается на себя.

Проекция прямой, не параллельной прямой проектирования, есть прямая, а проекция прямой, параллельной прямой проектирования, есть точка —точка пересечения проектируемой прямой и плоскости проекции.
p — плоскость проекции;
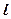

1) 
2) 
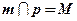
- Проекции параллельных прямых параллельны.
 |
 |
- Отношение длин проекций двух параллельных отрезков равно отношению длин проектируемых отрезков.
- Какой фигурой может быть проекция:
| a) прямой; b) плоскости; | c) треугольника; d) окружности? |
- Всегда ли проекции параллельных прямых суть параллельные прямые?
- На плоскости a даны две точки А и В. Отрезки
и
перпендикулярны к плоскости a . Найдите
, если
.
- Дан ромб с острым углом
и сторонами 25 см. Через одну из сторон проведена плоскость. Длина проекции другой стороны на эту плоскость равна 20 см. Найдите длины проекций диагоналей.
ПЛОЩАДЬ ПРОЕКЦИИ ПЛОСКОЙ ФИГУРЫ
Теорема: Площадь проекции плоского многоугольника на некоторую плоскость равна площади проектируемого многоугольника, умноженной на косинус угла между плоскостью многоугольника и плоскостью проекции.
1 этап: Проектируемая фигура – треугольник АВС, сторона которого АС лежит в плоскости проекции a (параллельна плоскости проекции a).

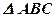

1. 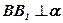
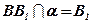
2. 
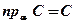

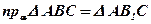
3. 

4. По теореме о трёх перпендикулярах 
ВD – высота 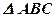

5. 


6. 



7. 
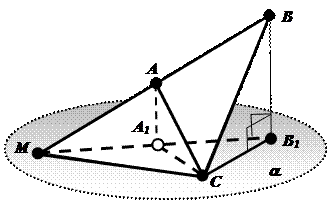
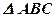

1. 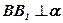
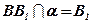
2. 
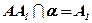
3. 
4. 



5. 




6. 
Этап: Проектируемая фигура – произвольный многоугольник.
Многоугольник разбивается диагоналями, проведёнными из одной вершины, на конечное число треугольников, для каждого из которых теорема верна. Поэтому теорема будет верна и для суммы площадей всех треугольников, плоскости которых образуют один и тот же угол с плоскостью проекции.
Замечание: Доказанная теорема справедлива для любой плоской фигуры, ограниченной замкнутой кривой.
1. Найти площадь треугольника, плоскость которого наклонена к плоскости проекции под углом 
2. Найти площадь треугольника, плоскость которого наклонена к плоскости проекции под углом 
3. Найти площадь треугольника, плоскость которого наклонена к плоскости проекции под углом 
4. Вычислить площадь трапеции, плоскость которой наклонена к плоскости проекции под углом 
5. Вычислить площадь проекции правильного шестиугольника со стороной 8 см, плоскость которого наклонена к плоскости проекции под углом 
6. Ромб со стороной 12 см и острым углом 

7. Ромб со стороной 20 см и диагональю 32 см образует с данной плоскостью угол 
8. Проекция навеса на горизонтальную плоскость есть прямоугольник со сторонами 


11. Упражнения по теме «Прямые и плоскости в пространстве»:
Стороны треугольника равны 20 см, 65 см, 75 см. Из вершины большего угла треугольника проведён к его плоскости перпендикуляр, равный 60 см. Найти расстояние от концов перпендикуляра до большей стороны треугольника.
2. Из точки, отстоящей от плоскости на расстоянии 

3. Сторона правильного треугольника равна 12 см. Точка М выбрана так, что отрезки, соединяющие точку М со всеми вершинами треугольника, образуют с его плоскостью углы 
4. Через сторону квадрата проведена плоскость под углом 
5. Катет равнобедренного прямоугольного треугольника наклонён к плоскости a, проходящей через гипотенузу, под углом 

6. Двугранный угол между плоскостями треугольников АВС и DВС равен 
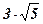
Контрольные вопросы по теме «Прямые и плоскости в пространстве»
1. Перечислить основные понятия стереометрии. Сформулировать аксиомы стереометрии.
2. Доказать следствия из аксиом.
3. Каково взаимное расположение двух прямых в пространстве? Дать определения пересекающихся, параллельных, скрещивающихся прямых.
4. Доказать признак скрещивающихся прямых.
5. Каково взаимное расположение прямой и плоскости? Дать определения пересекающихся, параллельных прямой и плоскости.
6. Доказать признак параллельности прямой и плоскости.
7. Каково взаимное расположение двух плоскостей?
8. Дать определение параллельных плоскостей. Доказать признак параллельности двух плоскостей. Сформулировать теоремы о параллельных плоскостях.
9. Дать определение угла между прямыми.
10. Доказать признак перпендикулярности прямой и плоскости.
11. Дать определения основания перпендикуляра, основания наклонной, проекции наклонной на плоскость. Сформулировать свойства перпендикуляра и наклонных, опущенных на плоскость из одной точки.
12. Дать определение угла между прямой и плоскостью.
13. Доказать теорему о трех перпендикулярах.
14. Дать определения двугранного угла, линейного угла двугранного угла.
15. Доказать признак перпендикулярности двух плоскостей.
16. Дать определение расстояния между двумя различными точками.
17. Дать определение расстояния от точки до прямой.
18. Дать определение расстояния от точки до плоскости.
19. Дать определение расстояния между прямой и параллельной ей плоскостью.
20. Дать определение расстояния между параллельными плоскостями.
21. Дать определение расстояния между скрещивающимися прямыми.
22. Дать определение ортогональной проекции точки на плоскость.
23. Дать определение ортогональной проекции фигуры на плоскость.
24. Сформулировать свойства проекций на плоскость.
25. Сформулировать и доказать теорему о площади проекции плоского многоугольника.
📸 Видео
Геометрия 8 класс : Отношение площадей подобных треугольниковСкачать

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Свойства проекций катетов | Геометрия 8-9 классыСкачать

Отношение площадей подобных треугольников | Геометрия 7-9 класс #58 | ИнфоурокСкачать

Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Теорема о площади проекцииСкачать

Геометрия 8. Урок 14 - Площадь треугольников. Формулы и задачи.Скачать

Урок 17. Площадь ортогональной проекции Задание 14 ЕГЭ по математике. Стереометрия с нуля.Скачать

Площадь треугольника. Как найти площадь треугольника?Скачать

Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать

Отношение площадейСкачать
СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Отношение площадей подобных треугольниковСкачать
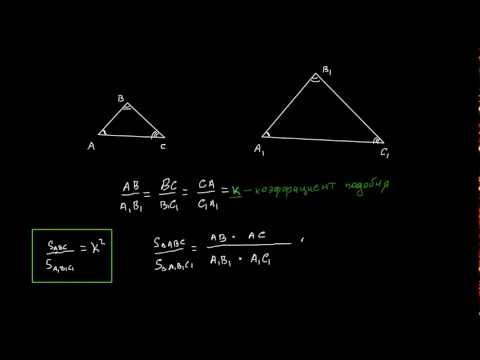
Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

134 Равнобедренный прямоугольный треугольник, проекция которого подобна ему, но меньшей площадиСкачать

Математика | Метрические соотношения в прямоугольном треугольникеСкачать

Способ замены (перемены) плоскостей проекции. Определение истинной величины отрезка и плоской фигурыСкачать

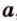
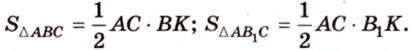
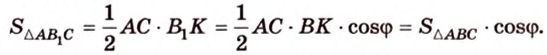
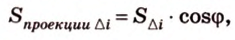
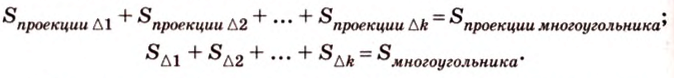
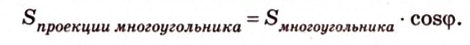
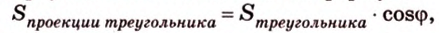
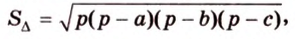
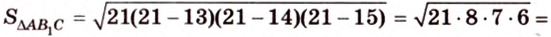
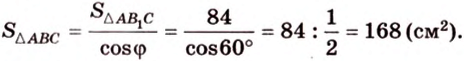
 При проектировании точка пространства отображается в точку плоскости проекции.
При проектировании точка пространства отображается в точку плоскости проекции.
 Проекция прямой, не параллельной прямой проектирования, есть прямая, а проекция прямой, параллельной прямой проектирования, есть точка —точка пересечения проектируемой прямой и плоскости проекции.
Проекция прямой, не параллельной прямой проектирования, есть прямая, а проекция прямой, параллельной прямой проектирования, есть точка —точка пересечения проектируемой прямой и плоскости проекции.

 и
и  перпендикулярны к плоскости a . Найдите
перпендикулярны к плоскости a . Найдите 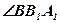 , если
, если  .
. и сторонами 25 см. Через одну из сторон проведена плоскость. Длина проекции другой стороны на эту плоскость равна 20 см. Найдите длины проекций диагоналей.
и сторонами 25 см. Через одну из сторон проведена плоскость. Длина проекции другой стороны на эту плоскость равна 20 см. Найдите длины проекций диагоналей.