Отношение периметров подобных треугольников доказательство

Что такое подобные треугольники?

Подобные треугольники определение

Подобные треугольники определение:

На рисунке изображены два подобных треугольника, у них углы соответственно равны, т.е. угол A равен углу A₁, угол B равен углу B₁, угол C равен углу C₁.

Сходственные стороны треугольников

Сходственные стороны треугольников пропорциональны:

здесь k называется коэффициентом подобия.

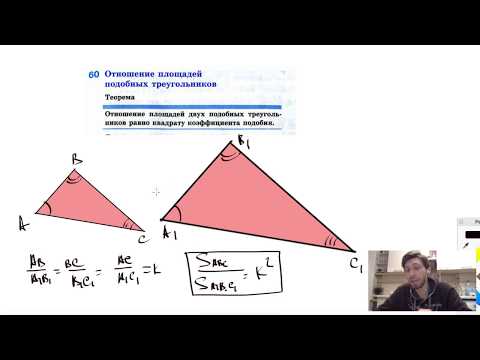
Отношение площадей подобных треугольников

Отношение площадей подобных треугольников равно квадрату коэффициента подобия:

Отношение периметров подобных треугольников

Отношение периметров подобных треугольников:

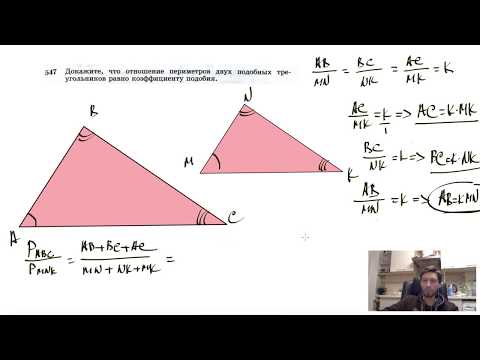
Докажем это утверждение. Пусть имеются два подобных треугольника ABC и A₁B₁C₁. По определению подобных треугольников их сходственные стороны пропорциональны:

Периметр треугольника ABC равен сумме длин его трёх сторон:

Сумма в скобках в правой части равенства представляет собой периметр треугольника A₁B₁C₁. Разделим обе части равенства на периметр A₁B₁ + B₁C₁ + A₁C₁. Получаем:

что и требовалось доказать. Итак, отношение периметров подобных треугольников равно коэффициенту подобия.

Для установления факта подобия двух треугольников используют признаки подобия треугольников:

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Докажите, что отношение периметров двух подобных треугольников равно коэффициенту подобия.

Видео:8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать

Ваш ответ

Видео:№547. Докажите, что отношение периметров двух подобных треугольников равно коэффициенту подобия.Скачать

решение вопроса

Видео:8 класс, 20 урок, Определение подобных треугольниковСкачать

Похожие вопросы

• Все категории
• экономические 43,288
• гуманитарные 33,620
• юридические 17,900
• школьный раздел 607,127
• разное 16,830

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

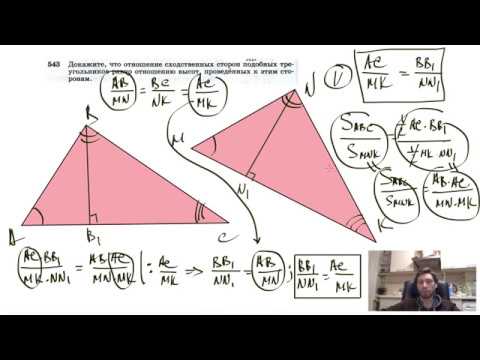
Видео:№543. Докажите, что отношение сходственных сторон подобных треугольников равноСкачать

Подобные треугольники

Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Определение

Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.

Коэффициентом подобия называют число k , равное отношению сходственных сторон подобных треугольников.

Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.

Видео:Первый признак подобия треугольников. Доказательство. 8 класс.Скачать

Признаки подобия треугольников

I признак подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

II признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Видео:Подобные треугольники. Отношение периметров.Скачать

Свойства подобных треугольников

• Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
• Отношение периметров подобных треугольников равно коэффициенту подобия.
• Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.

Видео:Геометрия 8 класс : Отношение площадей подобных треугольниковСкачать

Примеры наиболее часто встречающихся подобных треугольников

1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.

2. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –

3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.

Здесь вы найдете подборку задач по теме «Подобные треугольники» .

🎥 Видео

Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Отношение площадей подобных треугольников | Геометрия 7-9 класс #58 | ИнфоурокСкачать

Геометрия 8 класс (Урок№14 - Определение подобных треугольников. Отношение площадей подобных фигур.)Скачать

Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать

Второй признак подобия треугольников. Доказательство. 8 класс.Скачать

Отношение площадей подобных треугольниковСкачать

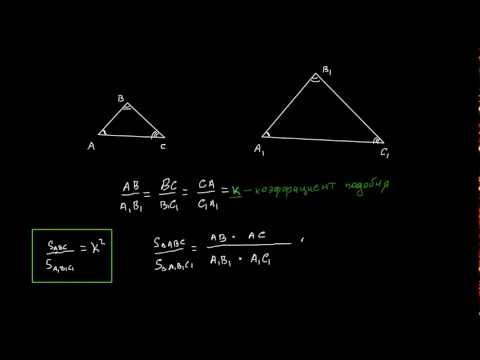
Решение задач на тему "Подобные треугольники". 8 классСкачать

Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

Отношение периметров подобных треугольников. ЗадачаСкачать

60. Отношение площадей подобных треугольниковСкачать

Отношение площадей подобных треугольников.Скачать