Разделы: Математика
Цели урока
- Обучающие. Опытным путем получить зависимость между длиной окружности и её диаметром, вывести формулы длины окружности и площади круга.
- Развивающие. Способствовать дальнейшему развитию внимания, наблюдательности, самоконтроля учащихся.
- Воспитательные. Воспитывать аккуратность и дисциплинированность школьников, умение работать в тишине, помогать товарищам.
Учащиеся должны иметь с собой картон, лист цветной бумаги, ножницы, нитки, циркуль, цветной карандаш, простой карандаш, клей-карандаш, калькулятор, линейку, фломастер.
Ход урока
В первую очередь актуализируются опорные знания, необходимые для выполнения лабораторной работы. Учащимся предлагается ответить на следующие вопросы:
- Что называют отношением двух величин?
- Как округлить десятичную дробь до десятых? До сотых?
- Чему равна площадь прямоугольника?
- Что такое окружность? Радиус? Диаметр?
- Если фигуру площадью S разделить на части с площадями S1 и S2, будет ли выполняться равенство S=S1+S2
- Если фигуру площадью S разделить на части и из них составить другую фигуру, будет ли её площадь равна площади первоначальной фигуры?
Учащиеся выполняют практические задания по команде учителя и записывают свои наблюдения (учитель может все проделывать на доске, если класс не достаточно подготовлен к самостоятельной работе, или предложить ученикам работать в парах).
- На картонном листе начертить окружность с произвольным радиусом, отметить её центр, записать значение радиуса в миллиметрах(R) и значение диаметра в миллиметрах(D).
- Провести клеем-карандашом по окружности и, пока клей не высох, проложить нитку точно по контуру окружности и аккуратно отрезать её на стыке.
- Снять нитку с картона и очень точно измерить её длину в миллиметрах. Этот размер назовем длиной окружности(L). Записать значение L.
- Найти отношение
с помощью калькулятора, округлить получившуюся дробь до тысячных, до сотых, до десятых, до целых. Сделать соответственные записи.
Далее ученики называют свои результаты и замечают, что, хотя окружности были построены у всех разные, отношения длины к диаметру получились примерно одинаковые.
Отношение длины окружности к её диаметру – величина постоянная и не зависит от размеров окружности. Число, выражающее это отношение, принято называть греческой буквой 

В глубокой древности считалось, что окружность ровно в 3 раза длиннее диаметра. Эти сведения содержатся в клинописных табличках Древнего Междуречья. Итак, первым приближением числа 
Три первые цифры числа 
Нужно только постараться
И запомнить все как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
С.Бобров. “Волшебный двурог”
Вывод формулы длины окружности.
Итак, мы имеем следующее соотношение: 



Учащимся предлагается выполнить несколько упражнений:
- D=6см, найти L.
- R=3дм3мм, найти L.
- L=6см, найти R.
- L=8
мм, найти R.
Вывод формулы площади круга.
Учащиеся выполняют практические задания по команде учителя (учитель может проделывать все на доске).
- На листе цветной бумаги начертить окружность с произвольным радиусом и провести фломастером по её контуру.
- Разделить круг с помощью линейки и карандаша на несколько секторов, затем разрезать его. (см. рис.1) Заметим, что не следует делить круг на меньшее, чем 8 секторов.
- В одном из секторов следует провести радиус, делящий его на 2 равных сектора, которые назовём крайними (см. рис.2) и отложить.
- На картонном листе провести горизонтальную прямую и приклеить вдоль неё сектора, как показано на рис.3. (На рис.3,а – круг разделен на 8 секторов, на рис.3,б – на 16 секторов). Крайние сектора приклеить по краям. Заметно, что получившаяся фигура при увеличении количества секторов становится очень похожей на прямоугольник. Значит, и её площадь можно найти по формуле площади прямоугольника. Ширина нашего прямоугольника равна радиусу окружности(R), а длина прямоугольника равна половине длины окружности (
). Площадь прямоугольника равна произведению длины на ширину, т. е. S=
, а т.к. L=2
R, значит S=
или S=
R 2 .
.Так как прямоугольник был составлен из частей круга, то их площади равны. Значит, площадь круга равна: S=

Применение формул для решения задач.
- Сравнить площади кругов с радиусами 3дм и 300мм.
- Найти площадь круга, если D=6см.
- Найти площадь круга, если L=10
.
- Сравнить площадь круга с R=5см с площадью квадрата со стороной 5см.
Следует отметить, что этот этап нужно включать в ход урока, если использован двухчасовой урок. В этом случае можно провести небольшую проверочную работу, которую учащиеся выполнят прямо на своих картонных листах. Учитель оценит правильность решения задач и аккуратность выполнения практической части.
В противном случае оценивается только практическая часть.
Комментарий: Данный урок является нетрадиционным, что особенно нравится детям любого возраста. Практика показывает, что получение или вывод формул “своими силами” прочно запоминается ввиду своей наглядности, четко простроенной цепочки выводов. Для учащихся 5-6 классов формулы длины окружности и площади круга – одни из первых, которые надо прочно запомнить. Так пусть дети их выведут сами!
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Практическая работа по математике 6 кл. Длина окружности.
Просмотр содержимого документа
«Практическая работа по математике 6 кл. Длина окружности.»
Тишевская Лилия Сергеевна
МБОУСШ №7, г.Волгодонск
Класс: 6 класс ( УМК Н.Я.Виленкин )
Тема урока: Длина окружности и площадь круга.
Тип урока: Комбинированный ( лабораторная работа и изучение нового материала).
Цель и задачи урока: Опытным путём получить приближенное значение числа 
Предметные: Вспомнить построение окружности и её элементов. Научиться отличать круг от окружности. Находить длину окружности расчетным и опытным путём. Находить площадь круга расчетным путём.
Метапредметные: Сформировать умение находить математические формулы и константы опытным путём.
Личностные: сформировать умение работать в коллективе, умение на практике разрешать проблемные ситуации, сформировать интерес к изучаемой теме.
1). Вспомним и закрепим понятия, связанные с окружностью и кругом, известные ученикам с 5-ого класса в виде опроса:
а) Что из себя представляет окружность?
Б) С помощью чего можно построить окружность?
В) Что такое круг?
Г) Что такое центр окружности?
Д) Что такое хорда?
Е) что такое радиус?
Ж) Что такое диаметр?
З) Как связаны диаметр и радиус окружности?
И) Что такое дуга окружности?
К) Что такое полуокружность и как ее получить?
Л) Что такое сектор окружности?
Ученики своими словами в свободной форме отвечают на вопросы учителя.
2). Учитель просит учеников с помощью циркуля и линейки начертить в тетради три окружности и самостоятельно отметить элементы окружности, которые только что вспомнили.
2. Лабораторная работа
Ученики раскладывают на парте заранее заготовленный материал и инструменты: 5 предметов цилиндрической формы, нитки, линейка , ножницы.
2) теоретическая часть.
А) Нахождение окружности в цилиндрическом предмете.
Б) длина окружности как периметр круга.
В) Создание проблемной ситуации.
Как помощью предметов на парте узнать длину окружности цилиндрических предметов?
Учитель выслушивает предположения учеников. (Если «опоясать» предмет ниткой, а потом распрямить её и измерить линейкой, то её длина будет приблизительно равна длине окружности) Обозначим её буквой С.
Как с помощью предметов на парте измерить диаметр окружности у цилиндрических предметов?
Учитель выслушивает предположения учеников ( На белом листе бумаги обвести круглый предмет, вырезать этот круг и согнуть пополам, измерить линию сгиба линейкой. Эта величина и будет диаметром ). Диаметр обозначим буквой d.
Установить есть ли связь между диаметром и длиной окружности.
Учитель поясняет, что ответ на этот вопрос может дать анализ результатов лабораторной работы.
Для этого нумеруем предметы и результаты измерений записываем в таблицу. При этом 4-ый столбец оставляем пустым.
Г) Выполнение практической части лабораторной работы. Ученики работают в парах.
Д) Анализ полученных измерений.
Ученики, используя таблицу, пытаются найти ответ на проблемную ситуацию, заданную в лабораторной работе. ( Если никто из учеников не догадался, учитель предлагает вспомнить последние пройденные темы или предлагает напрямую найти отношение длины окружности к её диаметру для каждого измерения)
Е) Вычислительная часть.
В 4-ый столбец считаем и записываем С:d с точностью до десятых.
Ж) Ученики приходят к выводу, что, несмотря на различные цифры во 2-ом и 3-ем столбцах, отношения этих величин приблизительно равны от 3,1 до 3,2.
Записывают вывод: опытным путём было установлено, что так как отношение длины окружности к её диаметру является одним и тем же числом, то длина окружности прямопропорциональна её диаметру. Таким образом связь установлена и проблемная ситуация разрешена.
З) Учитель рассказывает историческую справку о числе 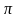
C:d= 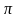

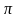
3. Вспомнив как связаны между собой радиус и диаметр окружности, учитель предлагает ученикам самостоятельно вывести формулу длины окружности через её радиус:
d=2r 
4. Учитель знакомит учеников с формулой площади круга:
5. Закрепление полученных знаний.
1) Решение задач у доски (решают два ученика) № 851, 855. УМК Н.Я. Виленкин.
Остальные ученики решают самостоятельно , сверяясь с доской.
2). № 854, 856. Решают самостоятельно.
6. Домашнее задание. П.24. №869, 870.
Анализ проведенного урока:
В ходе урока были реализованы все поставленные цели и задачи. В результате практической деятельности у учеников наблюдался повышенный интерес к разрешению проблемной ситуации.
В решении тех задач , где ученики применяли самостоятельно выведенные формулы, наблюдался больший процент успеха, чем в решении тех задач, в которых применялись формулы просто данные учителем
Видео:Длина окружности. Математика 6 класс.Скачать

Отношение длины окружности к ее диаметру
Тема: «Отношение длины окружности к ее диаметру»
Составила и провела: Трофимова Римма Ринатовна, учитель математики
МБОУ «Кривошеинская СОШ имени Героя Советского Союза Ф.М.Зинченко»
Тип урока: открытие новых знаний
Дидактическая цель: создать условия для формирования новой учебной информации.
Цель урока: Повторить определения окружности, круга, радиуса, диаметра, хорды, узнать, что обозначает число Пи.
— обучающие: узнать, какая величина является одинаковой для всех окружностей и узнать о происхождении числа Пи;
— развивающие: развивать умения анализировать, сравнивать, обобщать, делать выводы, развивать внимание;
— воспитательные: развивать познавательный интерес через игровые моменты (групповая работа) взаимоконтроля, взаимопроверки, способствовать пониманию необходимости интеллектуальных усилий для успешного обучения.
— личностные: развивать творческие способности через активные формы деятельности, умения сотрудничества и работы в группе.
По источникам знаний: словесные, наглядные;
По степени взаимодействия учитель-ученик: эвристическая беседа;
Относительно дидактических задач: подготовка к восприятию;
Относительно характера познавательной деятельности: репродуктивный, поисковый.
Оборудование:нитка, цилиндр 3 шт, 3 баночки из под крема, 3 стакана, планшетки-листки с указанием хода работы и правил работы в группе, листки с таблицами, листки для записи, доклад ученика с презентацией о происхождении числа Пи.
1.Мотивация учебной деятельности.
Создать благоприятный психологический настрой на работу
Здравствуйте, ребята!
Прошу занять свои места
Посмотрите. Всё ль в порядке:
Книжки, ручки и тетрадки.
Прозвенел сейчас звонок.
Девизом нашего урока будут слова: «Скажи мне — и я забуду, покажи мне — и я запомню, дай мне сделать — и я пойму»
2.Актуализация знаний и умений. Устный счет
Вычислить 1,6 : 8
Найдите отношения 123 к 3
Найдите среднее арифметическое 5 4 2 5
Выполните округление чисел До целого 54,8 20,28
До десятых 3,1504 50,49
До сотых 6,4723 210,8119
3. Целеполагание, постановка проблемы:
На столе расположены предметы кружка, баночка из под крема, ведро
– Что общего заметили у данных предметов? (заменить ведро на цилиндр) подвести к понятию окружность
– Что называется окружностью? назовите элементы окружности?
– Какой отрезок называется радиусом окружности?
– Какой отрезок называется диаметром окружности?
– Как связаны между собой радиус и диаметр окружности?
– Что такое хорда окружности ?
Расскажите, что у нас получается, когда мы чертим окружность?
– Как измерить длину окружности?
Молодцы! Итак, у нас появилось два понятия окружности, которые нам нужны будут на этом уроке – это диаметр и длина окружности.
Как вы думаете, какой будет тема нашего урока? (Связь диаметра и длины окружности)
Цель урока Найти связь диаметра и длины окружности. Сегодня на уроке мы будем открывать для себя новые знания. Узнаем о магическом числе, которое связывает диаметр и длину окружности. Число ПИ
4. Поиск путей решение проблемы: Как мы с вами уже заметили, предметы у нас разные, окружности, из которых они состоят – тоже разные и диаметр тоже разный. Давайте подумаем, может быть у них какое то значение равным?
Итак, наша задача, найти какое значение может быть равным у всех представленных окружностей
Работа в группах: Разобраться в этом нам поможет работа, которую мы сейчас с вами выполним. Давайте поделимся на группы, определитесь с ролями в группе (Приложение 1)
Вспомним, как работать в группе (Приложение 2)
Прочтите ход работы, которую вы сейчас будете выполнять.
Заполнить таблицу (Приложение 3)
Найденное среднее арифметическое каждая группа должна записать на доске.
По выполнению работы делаем вывод: во всех группах, получился примерно равный результат.
И так, ответим на вопрос, что общее у этих предметов, которые стоят на столе (какое значение является равным для них)? Число, равное отношению длины окружности к ее диаметру
Физминутка.Вы, наверное, устали?
Ну, тогда все дружно встали.
Рассчитались по порядку,
Приготовились к зарядке!
Итак, получили одинаковое значение — разделили длину окружности на ее диаметр. и получили число, которое носит специальное название – ЧИСЛО ПИ
5. Систематизация знаний: правило, чтоб нам запомнить число Пи Нужно только постараться
И запомнить всё, как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Часто для расчетов требуется не больше 2 знаков после запятой.
А в чем магия числа ПИ расскажет ваш товарищ.

Математики всего мира не прекращают вести исследования, связанные с числом Пи. Оно буквально окутано некой тайной. Некоторые теоретики даже полагают, что в нем заключена вселенская истина. Чтобы обмениваться знаниями и новой информацией о Пи, организовали Пи-клуб. Вступить в него непросто, нужно иметь незаурядную память. Так, желающих стать членом клуба экзаменуют: человек должен по памяти рассказать как можно больше знаков ч 
Сотруднику петербургского Музея городской скульптуры пришло в голову увековечить число «пи» на своем загородном участке под Приозерском. Но подошел к идее намного более творчески. Цифры числа он представил в виде деревянных столбиков разной высоты и цвета. Получилась такая математическая радуга.
6. Домашнее задание
Запишите домашнее задание учебник стр. 138-139 (читать), № 858устно, 865
7. Оценивание выставить оценку товарищам по группе. Сдать листочек учителю
На листочках разного цвета, где цвет соответствует точности знаний (красный – сомневаюсь, синий – уверен, что правильно) каждый записывает значение числа Пи, сколько запомнил. Затем проверяем
Понравился урок? Что нового узнали? Можно ли еще где нибудь применять полученные знания?
А завершить урок я хочу словами Роберта Сева:
Кто ничего не замечает,
Тот ничего не изучает.
Кто ничего не изучает,
Тот вечно хнычет и скучает! Спасибо за урок!
🌟 Видео
Длина окружности. Практическая часть - решение задачи. 6 класс.Скачать

Окружность. Круг. 5 класс.Скачать

Математика 6 класс (Урок№76 - Длина окружности. Площадь круга.)Скачать

Окружность и круг, 6 классСкачать

Длина окружности. Площадь круга - математика 6 классСкачать

Площадь круга. Практическая часть - решение задачи. 6 класс.Скачать
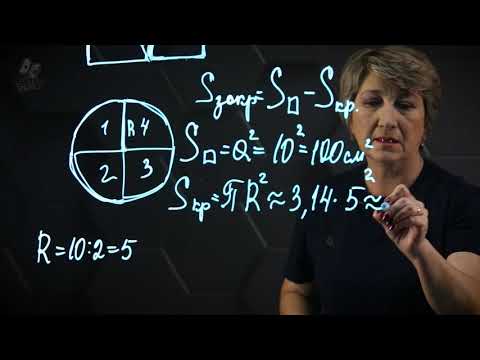
Отношение длины окружности к её диаметру. Площадь круга.Скачать

5 класс, 22 урок, Окружность и кругСкачать

Окружность. Круг. Практическая часть - решение задачи. 5 класс.Скачать

Площадь круга. Математика 6 класс.Скачать

Математика 3 класс (Урок№33 - Круг. Окружность (центр, радиус, диаметр)Скачать

КАК ИЗМЕРИТЬ ДЛИНУ ОКРУЖНОСТИ? · ФОРМУЛА + примеры · Длина окружности как найти? Математика 6 классСкачать

Длина окружности. Площадь круга, 6 классСкачать

КАК НАЙТИ ДИАМЕТР ОКРУЖНОСТИ, ЕСЛИ ИЗВЕСТНА ДЛИНА ОКРУЖНОСТИ? Примеры | МАТЕМАТИКА 6 классСкачать

ДЛИНА ОКРУЖНОСТИ. Видеоурок | МАТЕМАТИКА 6 классСкачать

КАК НАЙТИ ДЛИНУ ОКРУЖНОСТИ, ЕСЛИ ИЗВЕСТЕН ДИАМЕТР ИЛИ РАДИУС? Примеры | МАТЕМАТИКА 6 классСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

МЕРЗЛЯК-6. ДЛИНА ОКРУЖНОСТИ. ПЛОЩАДЬ КРУГА. ПАРАГРАФ-25Скачать


 мм, найти R.
мм, найти R.

 ). Площадь прямоугольника равна произведению длины на ширину, т. е. S=
). Площадь прямоугольника равна произведению длины на ширину, т. е. S= , а т.к. L=2
, а т.к. L=2 R, значит S=
R, значит S=  или S=
или S= R 2 .
R 2 .
 .
.