- Типы треугольников
- По величине углов
- По числу равных сторон
- Вершины углы и стороны треугольника
- Свойства углов и сторон треугольника
- Теорема синусов
- Теорема косинусов
- Теорема о проекциях
- Формулы для вычисления длин сторон треугольника
- Медианы треугольника
- Свойства медиан треугольника:
- Формулы медиан треугольника
- Биссектрисы треугольника
- Свойства биссектрис треугольника:
- Формулы биссектрис треугольника
- Высоты треугольника
- Свойства высот треугольника
- Формулы высот треугольника
- Окружность вписанная в треугольник
- Свойства окружности вписанной в треугольник
- Формулы радиуса окружности вписанной в треугольник
- Окружность описанная вокруг треугольника
- Свойства окружности описанной вокруг треугольника
- Формулы радиуса окружности описанной вокруг треугольника
- Связь между вписанной и описанной окружностями треугольника
- Средняя линия треугольника
- Свойства средней линии треугольника
- Периметр треугольника
- Формулы площади треугольника
- Формула Герона
- Равенство треугольников
- Признаки равенства треугольников
- Первый признак равенства треугольников — по двум сторонам и углу между ними
- Второй признак равенства треугольников — по стороне и двум прилежащим углам
- Третий признак равенства треугольников — по трем сторонам
- Подобие треугольников
- Признаки подобия треугольников
- Первый признак подобия треугольников
- Второй признак подобия треугольников
- Третий признак подобия треугольников
- Диагональ треугольника – формула
- Треугольник
- Прямоугольник
- Многоугольник
- Что мы узнали?
- Диагональ треугольника
- Треугольник
- Прямоугольник
- Многоугольник
- Что мы узнали?
Видео:Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

Типы треугольников
По величине углов
По числу равных сторон
Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°:
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β , тогда a > b
если α = β , тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 — 2 bc · cos α
b 2 = a 2 + c 2 — 2 ac · cos β
c 2 = a 2 + b 2 — 2 ab · cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Видео:Диагонали трапеции и точка их пересеченияСкачать

Медианы треугольника
Свойства медиан треугольника:
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
Медиана треугольника делит треугольник на две равновеликие части
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 1 2 √ 2 b 2 +2 c 2 — a 2
mb = 1 2 √ 2 a 2 +2 c 2 — b 2
mc = 1 2 √ 2 a 2 +2 b 2 — c 2
Видео:Трапеция. Отношение площадей треугольников. Свойства диагоналей трапецииСкачать

Биссектрисы треугольника
Свойства биссектрис треугольника:
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√ bcp ( p — a ) b + c
lb = 2√ acp ( p — b ) a + c
lc = 2√ abp ( p — c ) a + b
где p = a + b + c 2 — полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2 bc cos α 2 b + c
lb = 2 ac cos β 2 a + c
lc = 2 ab cos γ 2 a + b
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Высоты треугольника
Свойства высот треугольника
Формулы высот треугольника
ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Видео:Свойства диагоналей параллелограмма | Геометрия 8-9 классыСкачать

Окружность вписанная в треугольник
Свойства окружности вписанной в треугольник
Формулы радиуса окружности вписанной в треугольник
r = ( a + b — c )( b + c — a )( c + a — b ) 4( a + b + c )
Видео:Замечательное свойство трапеции | ЕГЭ по математике 2020Скачать

Окружность описанная вокруг треугольника
Свойства окружности описанной вокруг треугольника
Формулы радиуса окружности описанной вокруг треугольника
R = S 2 sin α sin β sin γ
R = a 2 sin α = b 2 sin β = c 2 sin γ
Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Связь между вписанной и описанной окружностями треугольника
Видео:Свойства диагоналей прямоугольника. Свойства диагоналей квадрата | Математика 4 класс #9 | ИнфоурокСкачать

Средняя линия треугольника
Свойства средней линии треугольника
MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC
MN || AC KN || AB KM || BC
Видео:Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Периметр треугольника
Периметр треугольника ∆ ABC равен сумме длин его сторон
Видео:Средняя линия треугольника и трапеции. 8 класс.Скачать

Формулы площади треугольника
Формула Герона
| S = | a · b · с |
| 4R |
Видео:Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

Равенство треугольников
Признаки равенства треугольников
Первый признак равенства треугольников — по двум сторонам и углу между ними
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Третий признак равенства треугольников — по трем сторонам
Видео:Площади треугольников с равным углом.Скачать

Подобие треугольников
∆MNK => α = α 1, β = β 1, γ = γ 1 и AB MN = BC NK = AC MK = k ,
где k — коэффициент подобия
Признаки подобия треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:Площадь ромба. Легче понять...Скачать
Диагональ треугольника – формула
Очень часто в начале изучения фигуры ученики путают значение диагонали прямоугольника и треугольника. Поэтому, чтобы не путаться в обозначениях, лучше разобраться в тематике раз и навсегда.
Видео:Соотношения между сторонами и углами треугольника. 7 класс.Скачать

Треугольник
Треугольник – это фигура, состоящая из трех сторон и трех углов. Треугольник имеет три характеризующих отрезка:
Треугольник не может иметь диагональ в принципе. Дело в том, что диагонали могут быть проведены только в многоугольниках, количество сторон которых больше 3.
Почему так? Потому что диагональ это отрезок, соединяющий противоположные вершины. В треугольнике противоположных вершин нет и быть не может. Существует сторона, противоположная вершине, но сами по себе вершины всегда смежные, т.е. соединенные одной стороной. Значит, диагонали треугольника не существует
Рис. 1. Три медианы в треугольнике.
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Прямоугольник
Прямоугольник – это первая фигура школьного курса математики, которая имеет диагональ. Так же, как диагональ имеет и квадрат.
Диагональ прямоугольника или квадрата всегда:
- Делит фигуру на две равных прямоугольных треугольника.
- В полученных треугольниках диагональ будет являться гипотенузой
- Диагональ будет равняться корню квадратному из суммы квадратов катетов согласно теореме Пифагора
Диагоналей в любом четырехугольнике 2, а в квадрате и прямоугольнике обе диагонали равны между собой.
При этом правило не касается других четырехугольников. Например, диагонали параллелограмма всегда неравны между собой. Запомните, если перед вами произвольный четырехугольник использовать утверждение о равенстве диагоналей без доказательства нельзя. Любое утверждение в геометрии, кроме аксиом должно быть доказано.
Кроме прямоугольника и квадрата равными диагоналями обладает ромб. При этом диагонали ромба перпендикулярны друг другу и, так же, как и диагонали квадрата и прямоугольника, точкой пересечения делятся пополам.
Видео:Найдите отношение отрезков диагоналиСкачать

Многоугольник
На самом деле, многоугольником может называться любая фигура с количеством углов, больше 2. По факту, любая фигура может называться многоугольником, поскольку 2 угла у замкнутой фигуры быть не может.
Рассмотрим многоугольники с количеством углов больше 4, поскольку четырехугольники мы уже рассмотрели.
Рис. 2. Диагонали многоугольника.
В многоугольнике, если он не является правильным, не получится решить задачу нахождения диагонали без дополнительных построений. В правильном многоугольнике все диагонали равны между собой и точкой пересечения делятся пополам.
Правильным многоугольником зовется фигура, все стороны и углы которой соответственно равны между собой.
Количество диагоналей можно посчитать, прикинув количество смежных и несмежных вершин. Смежными зовутся вершины, соединенные одним отрезком.
Например, в четырехугольнике у любой вершины есть две смежные вершины. Значит, для каждой вершины есть только одна диагональ. Диагональ соединяет две противоположные вершины, всего вершин 4, значит 4:2=2 – в любом четырехугольнике 2 диагонали.
Но этот способ не подойдет, если в задаче требуется подсчитать количество диагоналей у многоугольника с 5989 сторонами. Такая фигура вполне возможна в теории. На практике начертить ее весьма утомительно, как и подсчитать диагонали на чертеже. Поэтому была выведена формула числа диагоналей многоугольника:
$P=<n(n-3)over>$ – где n это число сторон многоугольника.
Проверим для квадрата:
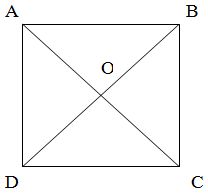
Рис. 3. Диагонали квадрата.
Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Что мы узнали?
Мы узнали, почему не существует формулы диагонали треугольника. Поговорили о том, что диагонали в принципе нет, и не может быть в многоугольниках с количеством сторон, меньше 3. Обсудили различные свойства диагоналей в различных фигурах.
Видео:Свойства прямоугольного треугольника. 7 класс.Скачать

Диагональ треугольника

Средняя оценка: 4.7
Всего получено оценок: 287.
Средняя оценка: 4.7
Всего получено оценок: 287.
Очень часто в начале изучения фигуры ученики путают значение диагонали прямоугольника и треугольника. Поэтому, чтобы не путаться в обозначениях, лучше разобраться в тематике раз и навсегда.
Видео:14. Свойства диагоналей прямоугольника и квадрата.Скачать

Треугольник
Треугольник – это фигура, состоящая из трех сторон и трех углов. Треугольник имеет три характеризующих отрезка:
Треугольник не может иметь диагональ в принципе. Дело в том, что диагонали могут быть проведены только в многоугольниках, количество сторон которых больше 3.
Почему так? Потому что диагональ это отрезок, соединяющий противоположные вершины. В треугольнике противоположных вершин нет и быть не может. Существует сторона, противоположная вершине, но сами по себе вершины всегда смежные, т.е. соединенные одной стороной. Значит, диагонали треугольника не существует
Прямоугольник
Прямоугольник – это первая фигура школьного курса математики, которая имеет диагональ. Так же, как диагональ имеет и квадрат.
Диагональ прямоугольника или квадрата всегда:
- Делит фигуру на две равных прямоугольных треугольника.
- В полученных треугольниках диагональ будет являться гипотенузой
- Диагональ будет равняться корню квадратному из суммы квадратов катетов согласно теореме Пифагора
Диагоналей в любом четырехугольнике 2, а в квадрате и прямоугольнике обе диагонали равны между собой.
При этом правило не касается других четырехугольников. Например, диагонали параллелограмма всегда неравны между собой. Запомните, если перед вами произвольный четырехугольник использовать утверждение о равенстве диагоналей без доказательства нельзя. Любое утверждение в геометрии, кроме аксиом должно быть доказано.
Кроме прямоугольника и квадрата равными диагоналями обладает ромб. При этом диагонали ромба перпендикулярны друг другу и, так же, как и диагонали квадрата и прямоугольника, точкой пересечения делятся пополам.
Многоугольник
На самом деле, многоугольником может называться любая фигура с количеством углов, больше 2. По факту, любая фигура может называться многоугольником, поскольку 2 угла у замкнутой фигуры быть не может.
Рассмотрим многоугольники с количеством углов больше 4, поскольку четырехугольники мы уже рассмотрели.

В многоугольнике, если он не является правильным, не получится решить задачу нахождения диагонали без дополнительных построений. В правильном многоугольнике все диагонали равны между собой и точкой пересечения делятся пополам.
Правильным многоугольником зовется фигура, все стороны и углы которой соответственно равны между собой.
Количество диагоналей можно посчитать, прикинув количество смежных и несмежных вершин. Смежными зовутся вершины, соединенные одним отрезком.
Например, в четырехугольнике у любой вершины есть две смежные вершины. Значит, для каждой вершины есть только одна диагональ. Диагональ соединяет две противоположные вершины, всего вершин 4, значит 4:2=2 – в любом четырехугольнике 2 диагонали.
Но этот способ не подойдет, если в задаче требуется подсчитать количество диагоналей у многоугольника с 5989 сторонами. Такая фигура вполне возможна в теории. На практике начертить ее весьма утомительно, как и подсчитать диагонали на чертеже. Поэтому была выведена формула числа диагоналей многоугольника:
$P=<n(n-3)over>$ – где n это число сторон многоугольника.
Проверим для квадрата:
Что мы узнали?
Мы узнали, почему не существует формулы диагонали треугольника. Поговорили о том, что диагонали в принципе нет, и не может быть в многоугольниках с количеством сторон, меньше 3. Обсудили различные свойства диагоналей в различных фигурах.


















