Открытый урок решение прямоугольных треугольников

Разделы: Математика

Цели урока:

• Образовательные: закрепить знание тригонометрических функций острого угла прямоугольного треугольника, научиться находить неизвестные элементы прямоугольного треугольника по известным двум его элементам, применять теоретические знания для решения практических задач.
• Развивающие: учиться грамотно формулировать свои мысли, развивать умение анализировать, обобщать, формировать правильную математическую речь.
• Воспитательные: воспитание интереса к математике, умения проявлять настойчивость в достижении цели.

Тип урока: урок изучения нового материала.

Вид урока: смешанный.

Прогнозируемый результат:

• знать определения тригонометрических функций в прямоугольном треугольнике, алгоритмы решения прямоугольных треугольников;
• уметь находить неизвестные элементы прямоугольного треугольника по известным двум его элементам.

Оборудование урока:

• Программное обеспечение: презентация Microsoft PowerPoint “Восхождение на математический олимп”;
• Техническое обеспечение: интерактивная доска ActivBoard.
• Раздаточный дидактический материал: карточки с задачами, опорные конспекты.

I. Организационный момент.

Проверка готовности учащихся к уроку. Приветствие учителя.

Сегодня нам будет нелегко: нам предстоит покорить математический Олимп. (Презентация, слайд № 1)

А тема нашего урока: “Решение прямоугольных треугольников”. Мы привыкли решать уравнение, задачи, примеры. а что значит: решить треугольник? (слайд № 2) Наша цель: узнать, что значит “решить треугольник” и научиться выполнять это на практике.

Маршрут восхождения на олимп указан на схеме. (слайд № 3) Номера его этапов — станций спрятались за знаками вопросов (в задачах на готовых чертежах). Найдите числа от 1 до 5, проложите маршрут и в путь! (слайд № 4)

II. Актуализация знаний.

1 этап. “1” спрятано в задаче:

Итак, первой у нас на пути станция Теоретическая (слайд №5)

Для начала проведём теоретическую разминку (разминка сопровождается показом сменяющихся слайдов)

Выберите верное утверждение: (слайды №6 -12)

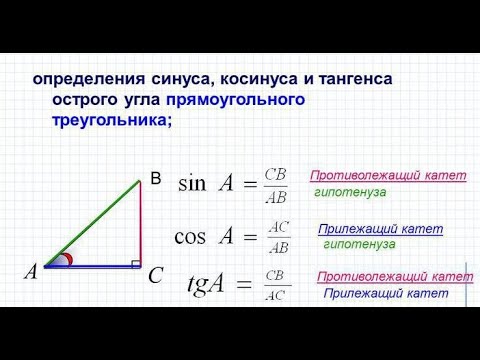
1. Синусом острого угла прямоугольного треугольника называется

Л — отношение прилежащего катета к гипотенузе.

Н — отношение противолежащего катета к прилежащему.

П — отношение противолежащего катета к гипотенузе.

2. Косинусом острого угла прямоугольного треугольника называется

Ф — отношение противолежащего катета к гипотенузе.

А — отношение прилежащего катета к гипотенузе.

О — отношение противолежащего катета к прилежащему.

3. Тангенсом острого угла прямоугольного треугольника называется

З — отношение противолежащего катета к гипотенузе

Н — отношение прилежащего катета к противолежащему

С — отношение противолежащего катета к прилежащему

А — отношение прилежащего катета к гипотенузе

4. Тангенс угла равен

Д — синусу этого угла

К — отношению синуса к косинусу этого угла

Г — отношению косинуса к синусу этого угла

П — косинусу этого угла

5. Катет, противолежащий углу a равен

У — произведению гипотенузы на тангенс угла a

М — произведению гипотенузы на косинус угла a

А — произведению гипотенузы на синус угла a

6. Катет, прилежащий к углу a равен

Л — произведению гипотенузы на косинус угла a

Э — произведению гипотенузы на синус угла a

Ю — произведению гипотенузы на тангенс угла a

7. Катет, противолежащий углу a равен

И — произведению гипотенузы на синус угла a

Ь — произведению другого катета на тангенс угла a

Р — произведению гипотенузы на тангенс угла a

Историческая справка: Блез Паскаль — знаменитый французский математик, механик, физик, литератор и философ (1623-1662). Один из основателей математического анализа, теории вероятностей и проективной геометрии. (слайд №13)

III. Объяснение нового материала.

2 этап. “2” спрятано в задаче:

Мы прошли первую станцию, и движемся ко второй. Вторая станция “Новые открытия”. (Презентация, слайды №14,15)

Учащимся предлагается решить задачу №1(слайд №16):

Дано: D РКМ, К = 90 0

РК = 1 см, РМ = 2 см.

Найти: Р, М, КМ.

1) Т.к. РК = 1/2 РМ, то М = 30 0 (св. прямоуг. треугольника)

2) ? Р = 90 0 — М = 60 0 (св. острых углов прямоуг. треугольника)

3) (по теореме Пифагора)

Ответ: 60 0 ; 30 0 ; см.

После того, как задача решена, перед учениками ставятся вопросы:

“Какие элементы прямоугольного треугольника были известны?”

(Гипотенуза и катет)

“Какие еще элементы треугольника мы нашли?”

(Второй катет и острые углы)

Определение (слайд №17):

Нахождение неизвестных элементов прямоугольного треугольника по известным двум его элементам называется решением прямоугольного треугольника.

Решить прямоугольный треугольник — значит вычислить все его стороны и углы по каким-либо данным, определяющим этот треугольник.

Для решения треугольников необходимо знать соотношения между сторонами и углами прямоугольного треугольника. Еще раз повторяем в виде формул (слайды №18,19):

Т. е. катет прямоугольного треугольника равен гипотенузе, умноженной на синус угла, противолежащего этому катету, или на косинус угла, прилежащего к нему.

Т. е. гипотенуза прямоугольного треугольника равна катету, деленному на синус угла, противолежащего этому катету, или на косинус угла, прилежащего к нему.

Далее рассматриваются возможные случаи задания прямоугольного треугольника по двум элементам, с комментариями учащихся заполняется таблица: (слайд №20)

IV. Первичное закрепление изученного материала. Выполнение упражнений.

3 этап. “3” спрятано в задаче:

Прошли станцию 2, впереди станция 3 “Практическая”. (слайды №21,22)

Решение задач: (слайд №23)

№2 Решить треугольник MNK.

Ученик, работающий у доски, определяет: какие элементы треугольника MNK надо найти. (Одновременно один ученик самостоятельно решает на меловой доске № 189 (2) из учебника.)

Дано: D МNК, К = 90 0

МК = 3 см, М = 30 0 .

Найти: МN, NК, N

N = 90 0 – 30 0 =60 0 .

Ответ:

Дано: ACB = 90 0

CD AB

A = a

Из треугольника АВС:

Из треугольника АСD:

Ответ: AC = m * cosа, BC = m * sinа, AD = m * cos 2 а

Дано: ABC = D = 90 0

CAB = a

ABD = b

Из треугольника АВС:

Из треугольника АВD:

V. Решение практических задач

4 этап. “4” спрятано в задаче:

Успешно преодолели 3 станцию,

И нас ждет станция 4 “С геометрией по жизни”.

Прямоугольный треугольник имеет широкое применение в повседневной жизни – многие геометрические и практические задачи сводятся к вычислению элементов прямоугольного треугольника, другими словами к решению прямоугольного треугольника. (слайд №28)

Задача № 5. (слайд №29)

Жители древней Америки, о которых вы возможно читали или ещё только прочитаете в книгах Фенимора Купера и Майн Рида, были искусными архитекторами. По всему континенту разбросаны величественные пирамиды майя. Самая загадочная из них пирамида Кукулькана на полуострове Юкатан в Мексике с храмом на вершине. Пирамида была построена в 11 веке, но триста лет спустя город, где она находится, был покинут своими жителями по невыясненным до сих пор причинам. Пирамиду поглотили джунгли.

Только в 19 веке древний город и сама пирамида были вновь обнаружены археологами. Началась реставрация, в ходе которой было выяснено, что пирамида обладает множеством оптических и акустических эффектов и несёт в себе астрономическую информацию. Но вначале учёные смогли измерить только длину её основания – 55,5 м и длину боковой грани – 31 м. (слайд №30) Затем им удалось измерить угол между этими отрезками – 52 градуса, после чего возник вопрос, а какова же высота пирамиды? Провести измерения высоты на местности не было никакой возможности, тогда на помощь археологам пришла математика, и они вычислили эту высоту.

Проведём высоту из вершины пирамиды и посмотрим – не появилась ли на слайде знакомая нам геометрическая фигура? (Треугольник) (слайд №31)

Определите вид этого треугольника. (Прямоугольный треугольник)

Что нам достаточно найти в этом треугольнике, чтобы достичь цели ? (Сторону АС)

Что нам известно в данном треугольнике? (Гипотенуза и острый угол В)

А так же мы знаем определения синуса, косинуса и тангенса острого угла. Поможет ли какое-нибудь из данных определений решить нашу проблему? (Синус)

Почему именно синус? (Он связывает вместе гипотенузу, угол и искомый катет)

Остался один вопрос – а можно ли найти значение синуса, зная только градусную меру угла? (слайд №32)

Ответ прост – можно, и это можно было сделать ещё более двух тысяч лет назад, во времена греческого астронома Гиппарха, который первым составил таблицы значений синуса, косинуса и тангенса. Сегодня все эти значения собраны в специальном сборнике Владимира Модестовича Брадиса “Четырёхзначные математические таблицы”.

Значение синуса возьмём из таблицы. (sin 52 o» 0,79) (слайд №33)

Как найдем катет АС? (Гипотенузу умножим на синус 52 градусов)

Вам остаётся только выполнить умножение (25,28 м)

Округлим ответ до целых. Итак, высота пирамиды индейцев майя? (25 м)

Задача №6 (слайд №34)

С самолета радируют капитану рыболовецкого судна, что самолет находится над косяком рыбы на высоте 1000 м. С судна определяют, что угол, под которым виден самолет над горизонтом, равен 26 0 . Используя таблицу тригонометрических функций, найдите расстояние от судна до косяка рыбы. В ответе укажите приближенное значение, выраженное целым числом.

Ученик у доски решает задачу, записывая решение на слайде № 35 презентации, где приготовлен чертеж:

ВС = 1000 * ctg 26 0 1000 * 2,050 2050 (м).

Резервная задача №7, можно предложить ее в качестве творческого домашнего задания. (слайд №36)

Высота пятиэтажного дома 15 м, а длина пожарной лестницы 30 м. На какой угол должна быть поднята лестница, чтобы достать до крыши дома, если её основание расположено на высоте 2 м от земли?

(Чертеж приготовлен на слайде презентации № 37.)

sin a = 13/30 0, 4333

a 25 0 36 / 26 0 .

Ответ: a 26 0 .

VI. Релаксация. Исторические сведения

5 этап. “5” спрятано в задаче:

Успешно преодолели 4 станцию, впереди станция 5 “Историческая”. (слайды №38,39)

Очень интересна история возникновения термина “синус”. (слайд №40)

Впервые зависимости между сторонами и углами прямоугольного треугольника, были найдены древнегреческим астрономом Гиппархом во 2 веке до н.э.

В 4 веке появился уже специальный термин в трудах по астрономии индийского учёного Ариабхаты, именем которого назван первый индийский спутник Земли. Поскольку вычисления синуса тогда были связаны с полухордами в окружности, очень похожими на тетиву натянутого лука, то Ариабхата так и назвал это отношение “полутетива” или “ардхаджива” на санскрите. Затем термин сократился до просто “джива”.

В 9 веке арабские учёные при переводе трудов Ариабхаты не стали оставлять буквальный смысл этого слова, а заменили созвучным арабским “джайб” — “впадина”, тем самым потеряв первоначальное значение термина.

Европейские же учёные добросовестно перевели “впадину” на латынь, получив слово “синус”, которым мы и пользуемся до сих пор.

История возникновения термина “косинус” не так интересна – это просто “дополнительный синус”.

“Тангенс” был известен ещё в 10 веке учёным Востока, а в Европе его открыли заново только в 14 веке, а в 16 он получил современное звучание, которое означает “касающийся”, что так же связано с окружностью.

Современные короткие обозначения были введены в 17 веке.

VII. Подведение итогов. Постановка домашнего задания.

Мы с вами успешно прошли все станции, и на вершине математического Олимпа водрузили наш флаг. (слайд №41)

Во время восхождения мы узнали, что значит решить треугольник, смогли попрактиковаться в этом, а также познакомились с историческими сведениями.

Запишите домашнее задание: параграф 12; № 188 (1,3), 189 (1) (слайд №42)

Выставление оценок за урок.

“Спасибо за урок! До свидания!” (слайд №43)

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Открытый урок по геометрии «Решение прямоугольных треугольников» (8 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Краткосрочное планирование урока

Предмет г еометрия 8 (А,В)класс

Решение прямоугольных треугольников.

Ученики знают понятие «решение прямоугольных треугольников»

Ученики умеют работать с дополнительной литературой, интернет-источниками, владеют первичными навыками ИКТ-технологий направленный для достижения учебной цели;
Ученики умеют переключаться с групповой на самостоятельную формы работы;
Ученики умеют выделять главное, умеют отвечать на вопросы высокого порядка.

Результат обучения для ученика А:

Ученики умеют работать с четырехзначными таблицами В.М.Брадиса .

Результат обучения для ученика В:

Ученики умеют применять теорему Пифагора при решении треугольников .

Результат обучения для ученика С:

Ученики умеют применять тригонометрические функции острого угла при решении прямоугольных треугольников;

Ученики умеют применять четырехзначные таблицы В.М.Брадиса при решении прямоугольных треугольников;

Я умею работать с четырехзначными таблицами В.М.Брадиса;
Я знаю понятие «решение прямоугольных треугольников»;
Я умею применять теорему Пифагора при решении треугольников;
Я умею применять тригонометрические функции острого угла при решении прямоугольных треугольников;
Я умею применять четырехзначные таблицы В.М.Брадиса при решении прямоугольных треугольников;

Основные ключевые идеи

1.. Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:

Чему равен tg 60°?

2. Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:

Чему равен sin 45°?

3 Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:

Чему равен cos 30°?

4.sin 2 а+ cos 2 а=1 основное тригонометрическое тождество синус квадрат альфа+ косинус квадрат альфа равно единица

Чему равен sin 30°?

5. В прямоугольном треугольнике тангенс острого угла равен отношению противолежащего катета к прилежащему катету, а, значит, tgα=sinα/cosα

Талицы Брадиса,учебник, сотовые телефоны, Листы А;, теради, карандаш, линейка,

наглядный, словесный, самостоятельный, групповой

1Организационный момент. Мотивация

Здравствуйте! Знаетели вы , что над каждым человеком горит его звезда? Как вы думаете , какая звезда горит над вами? Запишите на стикерах.

Приветствие. Дети записывают на стикерах свою звезду, затем оглашают.

2.Деление на группы.

Учитель делит учеников по уровням ( ученики С выбирают нумерованные ленты цветных стикеров, Ученики В выбирают ленты цветных стикеров ленты цветных стикеров, Ученики А выбирают ленты цветных стикеров ленты цветных стикеров.

Дети делятся на группы в соответствии с цветами

3.Правила работы группы дают математическое название своей группы

Учитель задаёт вопрос: Как нужно работать в группе?

Группы отвечают чётко и внятно не повторяясь по порядку соблюдая дисциплину и дают своё математическое название группы

4.Определение темы урока и запись числа, классная работа.

Учитель обращает внимание учеников на слайд с формулами и чертежом прямоугольного треугольника -Посмотрите и определите тему урока.

Определяют тему урока «Решение прямоугольных треугольников.»

5. Определение цели урока,

— Запишите в тетрадь свою цель на данный урок, озвучьте не повторясь. Хорошо!

Записывают свою цель на данный урок и озвучивают по порядку не повторясь

6. Мотивация на успешную работу

Знакомство с эпиграфом урока

И, так сегодня на уроке мы будем руководствоваться Эпиграфом урока: «Высшее назначение математики состоит
в том, чтобы находить скрытый порядок в хаосе, который нас окружает».
Н. Винер
Но́рберт Ви́нер — американский учёный, выдающийся математик и философ, основоположник кибернетики и теории искусственного интеллект

Дети обращают своё внимание.

8.Практическая часть: Задачи по теме «Теорема Пифагора»

Учитель знакомит с правилами игры «Миллионер», призывает слушать внимательно, ведб от этого зависит результат всей группы:

Кто вперёд поднимет руку, тот и отвечает.

Отвечать чётко, внятно, точно.

Слушать внимательно ответ .

1.Что называется тангенсом острого угла в прямоугольном треугольнике? Чему равен tg 60°?

2.Что называется синусом острого угла в прямоугольном треугольнике? Чему равен sin 45°?

3.Что называется косинусом острого угла в прямоугольном треугольнике? Чему равен cos 30°?

4.Какое равенство называют основным тригонометрическим тождеством? Чему равен sin 30°?

5.Как вычислить тангенс угла, если известны значения его синуса и косинуса? Чему равен tg 30°?

6.Какой треугольник называется египетским? Чему равен cos 45°?

Ответ: Египетский треугольник – прямоугольный треугольник с соотношением сторон 3:4:5.

7.Как переводится с древнегреческого слово «гипотенуза»? Почему? Чему равен cos 60°?

Ответ . ГИПОТЕНУЗА, гипотенузы, ж. (греч. hypoteinusa — натягивающая) (мат.). Сторона
прямоугольного треугольника, лежащая против прямого угла.

8.Является треугольник со сторонами 5см, 6см, 2см прямоугольным? Почему? Чему равен sin 45°?

9.Что означает слово «тригонометрия» как оно возникло? Чему равен tg 45°?

Ответ.Тригонометрия — математическая дисциплина изучающая зависимость между сторонами и углами треугольника.

Возникновение тригонометрии связано с землемерением, астрономией и строительным

Задачи по теме «Теорема Пифагора»

1 группа: Найти гипотенузу, если катеты равны 8 и 6 Ответ:с=10

2 группа: Найти катет, если две другие стороны 34 и 16 Ответ: в=30

3 группа: Найти гипотенузу, если катеты равны 12 и 5 Ответ:с=13

4 группа: Найти катет, если две другие стороны 25 и 15 Ответ: в=20

5 группа: Найти катет, если две другие стороны 26 и 10 Ответ: в=24

Ученики слушают внимательно и запоминают правила игры «Миллионер».

отвечают на вопросы устно

1. Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:

Чему равен tg 60°?

2. Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:

Чему равен sin 45°?

3 Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:

Чему равен cos 30°?

4.sin 2 а+ cos 2 а=1 основное тригонометрическое тождество синус квадрат альфа+ косинус квадрат альфа равно единица

Чему равен sin 30°?

5. В прямоугольном треугольнике тангенс острого угла равен отношению противолежащего катета к прилежащему катету, а, значит, tgα=sinα/cosα

Чему равен tg 30°?

Решают сообща и дружно, вносит каждый свою пользу длч достижения общей цели : правильное решение задачи

1.Оформление -3 балл

Чертёж Дано,Вопрос,Решение, Ответ ,Единицы измерения.

2. Подача информации:-1 балл

Точность , ясность, внятность.

3. Регламент -2 минуты -1 балл

9.Работа по таблице

« Математическая четырёхзначная таблица В.М.Брадиса »

Владимир Модестович Брадис- математик, педагог

1 группа: sin 52°48´

2 группа:. соs 34°24´

3 группа: tg 64°6´

4 группа:.с tg 42°12´

5 группа: соs 8° 30´

1.Оформление -3 балл

Решение, Ответ, Единицы измерения.

2. Подача информации:-1 балл

Точность , ясность, внятность.

3. Регламент -2 минуты -1 балл Используют таблицу В.М.Брадиса

10.Решение прямоугольных треугольников

Решение прямоугольных треугольников

Работа по учебнику стр 65 № 189 Найдите длину катета ВС прямоугольного треугольника АВС с прямым углом С если известно, что:

1 группа: АВ=10 см угол А=60°

2 группа:. АВ=12 см угол В=45°

3 группа: АС=5 угол А=45°

4 группа: АС=2 угол В=30°

5 группа: придумает свою задачу АВ=?см угол А= ?°

1.Оформление -3 балл

Решение, Ответ, Единицы измерения.

2. Подача информации:-1 балл

Точность , ясность, внятность.

3. Регламент -2 минуты -1 балл Используют учебник

Сверка правильных ответов на доске

11 Преобразование тригонометрических выражений

Преобразование тригонометрических выражений .

Рабочая тетрадь Издательство «Келешек» Стр 38 №119

Решают задачи у доски в тетради

Дети определяют свою мишень

§12 , придумать свою задачу на данную тему

ИД, презентация, учебник, чертёжные инструменты

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 963 человека из 80 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 309 человек из 70 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 676 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Решение прямоугольных треугольниковСкачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 555 239 материалов в базе

Другие материалы

• 12.02.2017
• 549
• 9

• 12.02.2017
• 562
• 0

• 12.02.2017
• 712
• 2

• 12.02.2017
• 661
• 1

• 12.02.2017
• 1086
• 12

• 12.02.2017
• 20039
• 92

• 12.02.2017
• 355
• 0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 12.02.2017 2384
• DOCX 35.9 кбайт
• 43 скачивания
• Рейтинг: 5 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Атаева Айгуль Мухамеджановна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет
• Подписчики: 0
• Всего просмотров: 23703
• Всего материалов: 11

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Решение прямоугольных треугольников. Практическая часть. 8 класс.Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Онлайн-семинар о развитии управляющих функций мозга ребенка

Время чтения: 1 минута

В России могут объявить Десятилетие науки и технологий

Время чтения: 1 минута

Петербургская учительница уволилась после чтения на уроке Введенского и Хармса

Время чтения: 3 минуты

У 76% российских учителей оклад ниже МРОТ

Время чтения: 2 минуты

В Рособрнадзоре рассказали, как будет меняться ЕГЭ

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:9 класс, 15 урок, Решение треугольниковСкачать

Открытый урок «Про прямоугольные треугольники»
методическая разработка по геометрии (8 класс) по теме

Применение теоремы Пифагора для решения задач

Видео:Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать

Скачать:

Видео:Решение прямоугольных треугольников. Практическая часть. 8 класс.Скачать

Предварительный просмотр:

Решение задач «Про прямоугольные треугольники»

Образовательные: Закрепить знание теоремы Пифагора, свойствапрямоугольного треугольника. Способствовать развитию навыка решения практических задач.

Развивающие : Развивать логическое мышление учащихся, при решении задач; Формировать умение строить и интерпретировать математическую модель некоторой реальной ситуации.

Воспитательные: Развивать внимание, умение слушать товарищей, работать в команде, анализировать результаты работы разных групп.

Тип урока : комбинированный.

Оборудование: Карточки для работы в паре;

карточки задания для работы в группе ,оценочный лист.

Стих шуточный ( о прям. треугольнике)

Я прочту одну историю, а вы ответите мне:

где и с кем могла произойти эта невероятная история?

О свойствах, какой фигуры, в ней говорится?

Доверчивости я пою хвалу,

Но и проверка тоже не обуза…

В определенном месте, на углу

Встречались катет и гипотенуза.

У катета она была одна.

Гипотенузу он любил, не веря сплетням,

Но, в тоже время, на углу соседнем

С другим встречалась катетом она.

И дело все закончилось конфузом-

Вот после этого и верь гипотенузам.

Тема сегодняшнего урока, звучит так:

Решение задач «Про прямоугольные треугольники»

Давайте определим цели и задачи урока:

Ответ: “эта история произошла в прямоугольном треугольнике”.

Развивать навыки решения задач.

2.Повторить соотношения в прям.треугольнике.

Что такое гипотенуза, катеты и какие их связывают отношения?

2.Проверка выполнения домашнего задания.

1.Заполнить таблицу, значений тригонометрических функций.

2.Вишнякова Екатерина стих о т.Пифагора.

Если дан нам треугольник,

И притом с прямым углом,

То квадрат гипотенузы

Мы всегда легко найдем

Катеты в квадрат возводим,

Сумму степеней находим

И таким простым путем

К результату мы придем.

Самопроверка по учебнику.

(всесторонняя проверка знаний учащихся).

«Лови ошибку».(в парах)

Работает с карточками в парах, на которых написаны утверждения, среди них есть ложные. Их нужно определить.

1.Если в треугольнике есть прямой угол , то треугольник называется равнобедренным. (И)

2.В треугольнике против большей стороны лежит больший угол. (И)

3.В прямоугольном треугольнике гипотенуза меньше катета.(Л)

4.В треугольнике против большего угла лежит большая сторона (И).

5 Синус-это отношение прилежащего катета к гипотенузе.(Л)

6.Сумма двух острых углов прямоугольного треугольника равна 90 0 . (И)

7.Сумма углов в любом треугольнике равна180 0 .(И)

8.Косинус –это противолежащий угол.(Л)

самопроверка с верными ответами.

соотношения в прямоугольном треугольнике.

4.Подготовка учащихся к активному и сознательному усвоению знаний.

Мы дали определения и записали формулы.

А для чего все-таки нужны синус, косинус, тангенс и котангенс?

Мы знаем, что сумма углов любого треугольника равна 180 0 .

Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора .

Получается, что зная два угла в треугольнике, можно найти третий.

Зная две стороны в прямоугольном треугольнике, можно найти третью.

Значит, для углов — свое соотношение, для сторон — свое.

А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?

В этом вам помогут тригонометрические функции синус и косинус.

5.Проверка понимания материала.

Работа в группах.

Задачи практического содержания

1. Лодка находится посередине реки. Глубина реки 4 м, длина якорного каната 5м. Как далеко отнесет течение реки лодку от места, куда был брошен якорь.

2. Найти длину шеста, необходимого для установления палатки.

Шест расположен посередине палатки. Расстояние от центра палатки до уголка пола равно 1м, длина наклонной 2 м.

Ответ:1 м.; 2м; 1,7 м

(На доску выводится чертеж пирамиды и демонстрируется модель.Эта задача из курса 10-го класса. А вы ее можете решить уже сейчас.

3.Охотник , стоящий на высоте 30 метров, видит зверя, стоящего во впадине , под углом 20 0 .Найдите расстояние между охотником и зверем.

4.Определите угол наклона шоссейной дороги, если на расстоянии 200 метров высота подъема 6 метров.

2 и 3 задание изобразить на рисунках.

Если соединить задачи, то можно решить задачу установки палатки, зная длину стороны квадратного пола и

В оценочных листах отметить результат.

Зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.

( Ученики по очереди дают

ответ на один из вопросов).

1. Своей работой на уроке я доволен / не доволен
2. Урок для меня показался коротким / длинным
3. Материал урока мне был полезен / бесполезен

Два окна имеют форму квадрата, одно – прямоугольное.

Стеклить окна нужно витражами, которые имеют форму

Укажите различные способы разбить четырехугольники

на равные между собой прямоугольные треугольники.

Задачи разных уровней сложности.

1. Найдите стороны ромба, если его диагонали равны 24 см и 18 см.

2. Найдите периметр прямоугольника, одна сторона которого равна 9 см, а диагональ – 15 см.

3. Стороны прямоугольника 8 см и 15 см. Найдите его диагонали.

1. В равнобокой трапеции основания равны 8 см и 14 см, боковая сторона – 5 см. Найдите высоту трапеции.

2. Высота равнобедренного треугольника равна 20 см, а его основание – 30 см. Найдите боковую сторону данного треугольника.

3 .Сторона равностороннего треугольника равна 183 см. Найдите биссектрису этого треугольника.

Внастоящеевремянарынкемобильнойсвязиидетбольшаяконкуренциясредиоператоров. Чемнадежнеесвязь, чембольшезонапокрытия, тембольшепотребителейуоператора. Пристроительствевышки (антенны) частоприходитсярешатьзадачу: какуюнаибольшуювысотудолжнаиметьантенна, чтобыпередачуможнобылоприниматьвопределенномрадиусе (например, радиусеR=200 км, еслиизвестно, чторадиусЗемлиравен 6380 км).

Пусть АВ=х, BC=R=200 км, ОС=r=6380 км. ОВ=ОА+АВ, следовательно: ОВ=r+х.

ИспользуятеоремуПифагора, получимответ 2,3 км.

Вдомезадуманопостроитьдвускатнуюкрышу (формавсечении). Какойдлиныдолжныбытьстропила, еслиизготовленыбалки AC=8 м, и AB=BF.

Треугольник ADC —равнобедренный АВ=ВС=4 м, BF=4 м, Еслипредположить, что FD=1,5 м, тогда:

А) Изтреугольника DBC:DB=2,5м DС=√4*4-2,5*2,5=√16+6,25=√22,25  4,7

Б) Изтреугольника ABF: AF=√l6+16=√32  5,7

Молниеотвод защищает от молнии все предметы, расстояние до которых от его основания не превышает его удвоенной высоты. Определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту.

По теореме Пифагора h*h>a*a+b*b, значит h>√(a*a+b*b) Ответ: h>√(a*a+b*b)

1.«Лови ошибку».(работа в парах)

Среди написанных утверждений, есть ложные и истинные.

Их нужно определить.

1.Если в треугольнике есть прямой угол , то треугольник называется равнобедренным.

2.В треугольнике против большей стороны лежит больший угол.

3.В прямоугольном треугольнике гипотенуза меньше катета.

4.В треугольнике против большего угла лежит большая сторона.

5 Синус-это отношение прилежащего катета к гипотенузе.

6.Сумма двух острых углов прямоугольного треугольника равна 90 0 .

7.Сумма углов в любом треугольнике равна180 0 .

8.Косинус –это противолежащий угол.

2.Задачи практического содержанияРабота в группах.

1. Лодка находится посередине реки. Глубина реки 4 м, длина якорного каната 5м. Как далеко отнесет течение реки лодку от места, куда был брошен якорь.

2. Найти длину шеста, необходимого для установления палатки.

Шест расположен посередине палатки. Расстояние от центра палатки до уголка пола равно 1м, длина наклонной 2 м.

Ответ: 1 м.; 2м; 1,7 м

3.Охотник , стоящий на высоте 30 метров, видит зверя, стоящего во впадине , под углом 20 0 .Найдите расстояние между охотником и зверем.

4.Определите угол наклона шоссейной дороги, если на расстоянии 200 метров высота подъема 6 метров.

Видео:Решение прямоугольных треугольников | Алгебра 10 класс #16 | ИнфоурокСкачать

По теме: методические разработки, презентации и конспекты

Тема: Прямоугольный треугольник. (второй урок по теме «Прямоугольный треугольник»)

Тема: Прямоугольный треугольник. (второй урок по теме «Прямоугольный треугольник») Приложение Презентация Цели урока: • сформировать понятия: прямоугольный треугольник, его кат.

7кл.Прямоугольный треугольник.Признаки равенства прямоугольных треугольников.

Урок-повторение по теме: «Прямоугольный треугольник. Теорема Пифагора. Соотношение между сторонами прямоугольного треугольника»

Применение групповых форм работы на уроках геометрии в 8 классе для развития познавательной активности учащихся и их коммуникативных умений.

Урок по теме: «Прямоугольный треугольник. Свойства прямоугольного треугольника.»

Первый урок по теме «Прямоугольный треугольник». Урок — исследование.

урок по геометрии«Прямоугольный треугольник и свойства прямоугольного треугольника»

Цель урока: Совершенствовать навыки решения задач на применение свойств прямоугольного треугольника.Задачи:обучающая — формировать знание свойств прямоугольного треугольника, уметь применять свойства .

Урок геометрии в 8 классе «Соотношения между сторонами и углами в прямоугольном треугольнике. Синус, косинус и тангенс острого угла в прямоугольном треугольнике»

Цель урока: ввести понятия синуса, косинуса и тангенса острого угла прямоугольного треугольника и ознакомить с правилом нахождения катета и гипотенузы, закреп.

Проверочная работа по теме «Свойства прямоугольных треугольников. Признаки равенства прямоугольных треугольников», 7 класс

Проверочная работа по теме «Свойства прямоугольных треугольников.Признаки равенства прямоугольных треугольников» предназначена для закрепления материала по данным темам. Проверяется и .

📽️ Видео

Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Решение прямоугольных треугольниковСкачать

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

РЕШЕНИЕ ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ . §18 геометрия 8 классСкачать

8 класс. Решение прямоугольных треугольниковСкачать

7 класс, 35 урок, Некоторые свойства прямоугольных треугольниковСкачать

7 класс, 36 урок, Признаки равенства прямоугольных треугольниковСкачать

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Геометрия. 8 класс. Решение прямоугольных треугольников /22.12.2020/Скачать

Решение прямоугольных треугольников. Синус, косинус, тангенс, котангенс. Решение задачСкачать

Геометрия. 8 класс. Решение прямоугольных треугольников /29.12.2020/Скачать

Геометрия. 8 класс. Решение прямоугольных треугольников /24.12.2020/Скачать

Решение прямоугольных треугольников. Синус, косинус, тангенс, котангенс - 8 класс геометрияСкачать