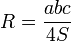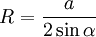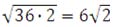Остроугольный равнобедренный треугольник bcd

4. MK ∙ KP = BK ∙ KC

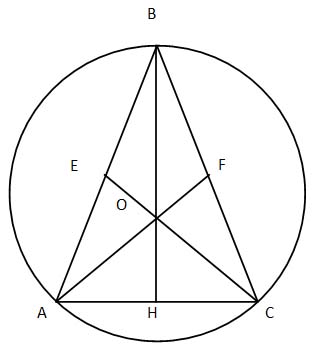
Задача 3: остроугольный равнобедренный треугольник BCD с основанием CD, равным 16, вписан в окружность с центром O и радиусом 10. Найдите площадь треугольника BOC.

1. ∆ BCD – равнобедренный, CD = 16, следовательно, DH = HC = 8

2. ∆ DOH – прямоугольный

По теореме Пифагора:

OH 2 = 10 2 – 8 2

OH 2 = 100 – 64 = 36

3. BH = BO + OH = 10 + 6 =16

4. По теореме Пифагора:

BC 2 = 16 2 + 8 2 = 256 + 64 = 320

8. S_BOC = 2 ∙ S_BOK = 2 ∙ 20 = 40

3.2 Задачи с окружностью, вписанной в треугольник

Задача 4: радиус окружности, вписанной в прямоугольный треугольник, равен 2 м, а радиус описанной окружности равен 5 м. Найдите больший катет треугольника.

2. Пусть AM = AK = x, MC = CL = y

По теореме Пифагора:

(x + 2) 2 + (y + 2) 2 = (x + y) 2

(x + 2) 2 + (10 – x + 2) 2 = (x + 10 – x) 2

(x + 2) 2 + (12 – x) 2 = 100

x 2 + 4x + 4 +144 – 24x + x 2 = 100

2x 2 – 20x + 148 = 100

2x 2 – 20x + 48 = 0

x 2 – 10x + 24 = 0

3. Так как нужно найти больший катет, то берем y = 6

Задача 5: окружность, вписанная в равнобедренный треугольник, касается его боковых сторон в точках K и A. Точка K делит сторону этого треугольника на отрезки 15 и 10, считая от основания. Найдите длину отрезка KA.

Дано: ∆ BCD – равнобедренный, K є BC, A є DC, BK = 15, KC = 10

1. CD = CB = BK + KC, CD = CB = 15 + 10 = 25

2. CK = CA = 10 (отрезки касательных, проведенные из одной точки), CB = CD, следовательно AD = CD – CA, AD = 25 – 10 = 15

3. BE = BK = 15, DE = DA = 15 (отрезки касательных, проведенные из одной точки), следовательно BD = 15 + 15 = 30

∆ CBD (ﮮC – общий, CK : CB = CA : CD), следовательно KA : BD = CA : CD, KA : 30 = 10 : 25, KA = 10 ∙ 30 : 25 = 12

BC = 18 + 12 = 30 (м)

Ответ: 30 м – диаметр описанной окружности

3.3. Задачи с окружностью, описанной около четырехугольника

Задача 6: в равнобедренной трапеции основания 21 и 9 сантиметров, высота – 8 сантиметров. Найти радиус описанной окружности.

1. Проведем серединные перпендикуляры к основаниям Н и К, тогда центр окружности О лежит на прямой НК.

2. АО=ОВ=R. Точка О делит отрезок НК на две части: пусть НО = х, тогда ОК = 8 – х.

3. АО 2 = АК 2 + КО 2 ; ОВ 2 = ВН 2 + НО 2 ;

Видео:№263. Высоты, проведенные к боковым сторонам АВ и АС остроугольного равнобедренного треугольникаСкачать

Остроугольный равнобедренный треугольник bcd

ТЕМА УРОКА: Окружность, описанная около треугольника.

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Содержание

Цели урока:

• Углубить знания по теме «Описанная окружности в треугольниках»

Задачи урока:

• Систематизировать знания по этой теме
• Подготовиться к решению задач повышенной сложности.

План урока:

1. Введение.
2. Теоретическая часть.
3. Для треугольника.
4. Практическая часть.

Введение.

Тема «Вписанные и описанные окружности в треугольниках» является одной из самых сложных в курсе геометрии. На уроках ей уделяется очень мало времени.

Геометрические задачи этой темы включаются во вторую часть экзаменационной работы ЕГЭ за курс средней школы.
Для успешного выполнения этих заданий необходимы твердые знания основных геометрических фактов и некоторый опыт в решении геометрических задач.

Теоретическая часть.

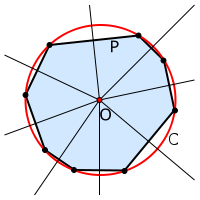
Описанная окружность многоугольника — окружность, содержащая все вершины многоугольника. Центром является точка (принято обозначать O) пересечения серединных перпендикуляров к сторонам многоугольника.

Центр описанной окружности выпуклого n-угольника лежит в точке пересечения серединных перпендикуляров к его сторонам. Как следствие: если рядом с n-угольником описана окружность, то все серединные перпендикуляры к его сторонам пересекаются в одной точке (центре окружности).
Вокруг любого правильного многоугольника можно описать окружность.

Для треугольника.

Окружность называется описанной около треугольника, если она проходит через все его вершины.

Вокруг любого треугольника можно описать окружность, притом только одну. Её центром будет являться точка пересечения серединных перпендикуляров.

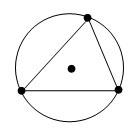
У остроугольного треугольника центр описанной окружности лежит внутри, у тупоугольного — вне треугольника, у прямоугольного — на середине гипотенузы.

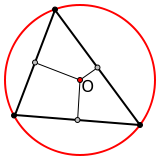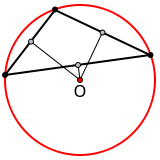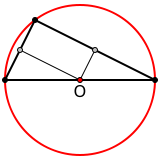Остроугольный	Тупоугольный	Прямоугольный

Радиус описанной окружности может быть найден по формулам:

Где:
a,b,c — стороны треугольника,
α — угол, лежащий против стороны a,
S — площадь треугольника.

Файл:T.gif Теорема. Теорема о центре окружности, описанной около треугольника.

Центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров к сторонам треугольника, проведенных через середины этих сторон.

Пусть ABC – данный треугольник и O – центр окружности описанной около данного треугольника. Δ AOB – равнобедренный ( AO = OС как радиусы). Медиана OD этого треугольника одновременно является его высотой. Поэтому центр окружности лежит на прямой, перпендикулярной стороне AC и проходящей через ее середину. Так же доказывается, что центр окружности на перпендикулярах к другим сторонам треугольника.

Рассмотрим подробнее этот случай.
Дано:

ΔABC, окр (О, ОА) — описана около ΔABC

т.О — точка пересечения серединных перпендикуляров к сторонам ΔABC

1. ΔAОC — равнобедренный, т.к. ОА=ОС (как радиусы)
2. ΔAОC — равнобедренный, перпендикуляр OD — медиана и высота, т.е. т.О лежит на серединном перпендикуляре к стороне АС
3. Аналогично доказывается, что т.О лежит на серединных перпендикулярах к сторонам АВ и ВС

Что и требовалось доказать.

Прямую, проходящую через середину отрезка перпендикулярно к нему, часто называют серединным перпендикуляром. В связи с этим иногда говорят, что центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к сторонам треугольника.

Файл:T.gif Теорема. Теорема об окружности, описанной около треугольника. Около любого треугольника можно описать окружность.

АВС — данный треугольник; О — точка пересечения серединных перпендикуляров (рис. 31).

О — центр окружности, вписанной в АВС.

Обозначим буквой О точку пересечения серединных перпендикуляров к его сторонам и проведем отрезки ОА, ОВ и ОС. Так как точка О равноудалена от вершин треугольника АВС, то ОА=OB=ОС. Поэтому окружность с центром О радиуса ОА проходит через все три вершины треугольника и, значит, является описанной около треугольника ABC.

Отметим, что около треугольника можно описать только одну окружность. В самом деле, допустим, что около треугольника можно описать две окружности. Тогда центр каждой окружности равноудален от вершин треугольника и, значит, совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника. Следовательно, эти окружности совпадают.

Практическая часть.

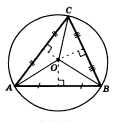
Около равнобедренного треугольника с основанием AC и углом при основании 75˚ описана окружность с центром O.

Найдите ее радиус, если площадь треугольника BOC равна 16.

∆ ABC – равнобедренный, AC – основание, ∠ ACB = 75˚,
площадь ∆ BOC равна 16
Найти:

Радиус описанной окружности

Проведем медианы AF, CE, BH
∆ ABC – равнобедренный, BH – медиана, следовательно, BH – высота, а значит ∆ HBC – прямоугольный
ﮮ HBC = 90˚ — ﮮ ACB, ﮮ HBC = 90˚ — 75˚ = 15˚
BO = OC = R, следовательно, ∆ BOC – равнобедренный, значит ﮮHBC = ﮮECB = 15˚
ﮮ COB = 180˚ — (ﮮ HBC + ﮮECB), ﮮ COB = 180˚ — (15˚ + 15˚) = 150˚

S = 1/2 ∙ BO ∙ OC ∙ sin ﮮ BOC (теорема о площади треугольника),

S_BOC = 1/2 ∙ R ∙ R ∙ sin 150˚ = 1/2 ∙ R ∙ R ∙ 1/2 = 1/4 ∙ R 2 ;

R 2 = 16 : 1/4 = 64;

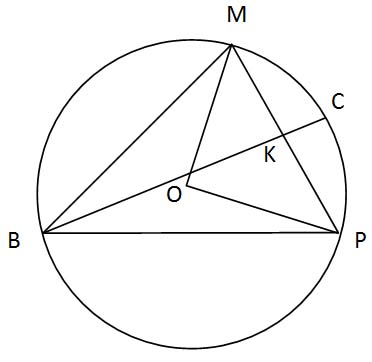
Треугольник BMP с углом B, равным 45˚, вписан в окружность радиуса 6.

Найдите длину медианы BK, если BK пересекает окружность в точке C и CK = 3.

Решение:
ﮮ MOP = 2 ﮮMBP
ﮮ MOP = 2 ∙ 45˚ = 90˚, следовательно, ∆ MOP – прямоугольный
MP 2 = OM 2 + OP 2
MP 2 = 62 + 62 = 36 + 36 = 36 ∙ 2
MP =
MK = KP = 0,5 ∙ MP
MK = KP = 0,5 ∙ =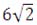
MK ∙ KP = BK ∙ KC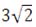
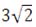
∙ = BK ∙ 3
BK ∙ 3 = 9 ∙ 2
BK ∙ 3 = 18
BK = 6
Ответ: BK = 6

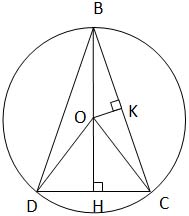
Остроугольный равнобедренный треугольник BCD с основанием CD, равным 16, вписан в окружность с центром O и радиусом 10. Найдите площадь треугольника BOC.

Интересный факт:

Софизм – это последовательность высказывания, рассуждений, построений, содержащая скрытую ошибку, за счет чего удается сделать неверный вывод. Задача обычно заключается в том, чтобы найти ошибку в рассуждениях.

Найдите ошибку в «доказательстве» того «странного» факта, что окружность имеет два центра.

Пусть даны две непараллельные прямые a и b. Из точек А и В этих прямых поставим перпендикуляры до пересечения в точке С. Через три точки А, В и С проведем окружность, пересекающую прямую а в точке М, а прямую b в точке N. По построению ∠MAC = ∠NBC = 900, значит, эти углы опираются на диаметры МС и NC построенной окружности. Середины этих диаметров – точки О1 и О2 – центры одной и той же окружности.

Ошибка в следующем:

∠MAC = ∠NBC = 900 (по построению). Эти углы являются вписанными и опирающимися на одну и туже дугу (в нашем случае, на полуокружность), поэтому точки О1 и О2 совпадают и лежат на отрезке DC (DC – биссектриса угла ADB).

1. Сформулируйте определение окружности и круга?
2. Что такое Софизмы?
3. Какая разница между диаметром и радиусом?
4. Как найти радиус окружности какая описана около треугольника?

Список использованных источников:

1. Урок на тему «Наглядная геометрия» Автор: Самылина Марина Валентиновна., г. Киев
2. «Единый государственный экзамен 2006. Математика. Учебно-тренировочные материалы для подготовки учащихся/ Рособрнадзор, ИСОП – М.: Интеллект-Центр, 2006»
3. Мазур К. И. «Решение основных конкурсных задач по математике сборника под редакцией М. И. Сканави»
4. Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина «Геометрия, 7 – 9: учебник для общеобразовательных учреждений»

Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на Образовательном форуме, где на международном уровне собирается образовательный совет свежей мысли и действия. Создав блог, Вы не только повысите свой статус, как компетентного преподавателя, а и сделаете весомый вклад в развитие школы будущего. Гильдия Лидеров Образования открывает двери для специалистов высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.

Видео:№142. Равнобедренные треугольники ADC и BCD имеют общее основание DC. Прямая АВ пересекает отрезокСкачать

Вписанные и описанные окружности в треугольниках и четырехугольниках

Работу выполнил ученик 9 «Б» класса

МОУ СОШ № 21 Свистов Иван

Руководитель: учитель математики МОУ СОШ № 21

2. Теоретическая часть:

2.1. Вписанная окружность

2.2. Описанная окружность

2.3. Взаимное расположение прямой и окружности

2.3. Площади фигур

2.5. Свойства прямоугольного треугольника

3. Практическая часть:

3.1. Задачи с окружностью, описанной около треугольника

3.2. Задачи с окружностью, вписанной в треугольник

3.3. Задачи с окружностью, описанной около четырехугольника

3.4. Задачи с окружностью, вписанной в треугольник

Тема «Вписанные и описанные окружности в треугольниках и четырехугольниках» является одной из самых сложных в курсе геометрии. На уроках ей уделяется очень мало времени.

Геометрические задачи этой темы включаются во вторую часть экзаменационной работы ЕГЭ за курс средней школы.

Для успешного выполнения этих заданий необходимы твердые знания основных геометрических фактов и некоторый опыт в решении геометрических задач.

Углубить знания по теме «Вписанная и описанная окружности в треугольниках и четырехугольниках»

Систематизировать знания по этой теме

Подготовиться к решению задач повышенной сложности ЕГЭ

Определение: если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности.

Теорема: в любой треугольник можно вписать окружность, и притом только одну.

Центр окружности, вписанной в треугольник, находится на пересечении биссектрис треугольника.

Свойство: в любом описанном четырехугольнике суммы противоположных сторон равны.

Признак: если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.

Определение: если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность.

Теорема: около любого треугольника можно описать окружность, и притом только одну.

Центр окружности, описанной около треугольника, находится на пересечении серединных перпендикуляров.

Свойство: в любом вписанном четырехугольнике сумма противоположных углов равна 180˚.

Признак: если сумма противоположных углов четырехугольника равна 180˚, то около него можно описать окружность.

Взаимное расположение прямой и окружности:

AB – касательная, если OH = r

AB ┴ OH (OH – радиус, проведенный в точку касания H)

Свойство отрезков касательных, проведенных из одной точки:

Площадь параллелограмма

· Площадь параллелограмма равна произведению его основания на высоту:

· Площадь параллелограмма равна произведению двух соседних его сторон ​на синус угла между ними:

ü Площадь треугольника равна половине произведения двух его сторон на синус угла между ними:

ü Площадь треугольника равна половине произведения его основания на высоту:

ü Площадь прямоугольного треугольника равна половине произведения его катетов:

ü Если высоты двух треугольников равны, то их площади относятся как основания.

ü Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы:

Площадь трапеции равна произведению полусуммы её оснований на высоту:

Теорема: отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой:

Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы:

Теорема: сумма углов треугольника равна 180°

Основное тригонометрическое тождество: sin2 A + cos2 A = 1

Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними: a2 = b2 + c2 – 2bc ∙ cos A

Свойство хорд: если две хорды окружности, AB и CD пересекаются в точке M, то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM ∙ MB = CM ∙ MD.

Теорема Пифагора:

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: c2 = a2 + b2

Медиана (от лат. mediana — средняя), отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.

Задача 1: Около равнобедренного треугольника с основанием AC и углом при основании 75˚ описана окружность с центром O. Найдите ее радиус, если площадь треугольника BOC равна 16.

Дано: ∆ ABC – равнобедренный, AC – основание, ﮮ ACB = 75˚,

площадь ∆ BOC равна 16

Найти: радиус описанной окружности

1. Проведем медианы AF, CE, BH

2. ∆ ABC – равнобедренный, BH – медиана, следовательно, BH – высота, а значит ∆ HBC – прямоугольный

3. ﮮ HBC = 90˚ — ﮮ ACB, ﮮ HBC = 90˚ — 75˚ = 15˚

4. BO = OC = R, следовательно, ∆ BOC – равнобедренный, значит ﮮHBC = ﮮECB = 15˚

5. ﮮ COB = 180˚ — (ﮮ HBC + ﮮECB), ﮮ COB = 180˚ — (15˚ + 15˚) = 150˚

6. S = ∙ BO ∙ OC ∙ sin ﮮ BOC (теорема о площади треугольника), SBOC = ∙ R ∙ R ∙ sin 150˚ = ∙ R ∙ R ∙ = ∙ R2 ; ∙ R2 = 16; R2 = 16 : = 64; R = = 8

Задача 2: треугольник BMP с углом B, равным 45˚, вписан в окружность радиуса 6. Найдите длину медианы BK, если BK пересекает окружность в точке C и CK = 3.

1. ﮮ MOP = 2 ﮮMBP

ﮮ MOP = 2 ∙ 45˚ = 90˚, следовательно, ∆ MOP – прямоугольный

2. MP2 = OM2 + OP2

MP2 = 62 + 62 = 36 + 36 = 36 ∙ 2

MP =

3. MK = KP = 0,5 ∙ MP

MK = KP = 0,5 ∙ =

4. MK ∙ KP = BK ∙ KC

= BK ∙ 3

Задача 3: остроугольный равнобедренный треугольник BCD с основанием CD, равным 16, вписан в окружность с центром O и радиусом 10. Найдите площадь треугольника BOC.

1. ∆ BCD – равнобедренный, CD = 16, следовательно, DH = HC = 8

2. ∆ DOH – прямоугольный

По теореме Пифагора:

OH2 = 100 – 64 = 36

3. BH = BO + OH = 10 + 6 =16

4. По теореме Пифагора:

BC2 = 162 + 82 = 256 + 64 = 320

BC =

6. SBHC =

7.

8. SBOC = 2 ∙ SBOK = 2 ∙ 20 = 40

Задача 4: радиус окружности, вписанной в прямоугольный треугольник, равен 2 м, а радиус описанной окружности равен 5 м. Найдите больший катет треугольника.

2. Пусть AM = AK = x, MC = CL = y

По теореме Пифагора:

(x + 2)2 + (y + 2)2 = (x + y)2

(x + 2)2 + (10 – x + 2)2 = (x + 10 – x)2

(x + 2)2 + (12 – x)2 = 100

x2 + 4x + 4 +144 – 24x + x2 = 100

2×2 – 20x + 148 = 100

2×2 – 20x + 48 = 0

x = 6 x = 4

3. Так как нужно найти больший катет, то берем y = 6

Задача 5: окружность, вписанная в равнобедренный треугольник, касается его боковых сторон в точках K и A. Точка K делит сторону этого треугольника на отрезки 15 и 10, считая от основания. Найдите длину отрезка KA.

Дано: ∆ BCD – равнобедренный, K є BC, A є DC, BK = 15, KC = 10

1. CD = CB = BK + KC, CD = CB = 15 + 10 = 25

2. CK = CA = 10 (отрезки касательных, проведенные из одной точки), CB = CD, следовательно AD = CD – CA, AD = 25 – 10 = 15

3. BE = BK = 15, DE = DA = 15 (отрезки касательных, проведенные из одной точки), следовательно BD = 15 + 15 = 30

∆ CBD (ﮮC – общий, CK : CB = CA : CD), следовательно KA : BD = CA : CD, KA : 30 = 10 : 25, KA = 10 ∙ 30 : 25 = 12

Задача 6: периметр прямоугольного треугольника равен 72 м, а радиус вписанной в него окружности – 6 м. Найдите диаметр описанной окружности.

Дано: ∆ ABC – прямоугольный, P = 72 м, r = 6 м

1. DO = OF = OE = r = 6 м, следовательно AD = AF = 6 м

2. FC = EC, BD = BE (отрезки касательных, проведенные из одной точки)

3. Пусть BD = x, FC = y, тогда AB = x + 6, AC = y + 6, BC = x + y

4. По теореме Пифагора AB2 + AC2 = BC2

5. P = AB + BC + AC, P = x + 6 + x + y + y + 6 = 2x + 2y + 12

6. 2x + 2y + 12 = 72

(x + 6)2 + (y + 6)2 = (x + y)2

x2 + 12x + 36 + y2 + 12y + 36 = x2 + 2xy + y2

x + y = 30

12x – 2xy + 12y + 72 = 0 I: 2

y = 30 – x

6x – xy + 6y + 36 = 0

6x – x(30 – x) + 6(30 – x) + 36 = 0

6x – 30x + x2 + 180 – 6x + 36 = 0

x2 – 30x + 216 = 0

D = (-30)2 – 4 ∙ 1 ∙ 216 = 900 – 864 = 36

x1 = = = 18, x2 = = = 12

y = 30 – x

BC = 18 + 12 = 30 (м)

Ответ: 30 м – диаметр описанной окружности

Задача 7: в равнобедренной трапеции основания 21 и 9 сантиметров, высота – 8 сантиметров. Найти радиус описанной окружности.

1. Проведем серединные перпендикуляры к основаниям Н и К, тогда центр окружности О лежит на прямой НК.

2. АО=ОВ=R. Точка О делит отрезок НК на две части: пусть НО = х, тогда ОК = 8 – х.

3. АО2 = АК2 + КО2; ОВ2 = ВН2 + НО2;

так как ОА2=ОВ2, получим:

АК2 + КО2 = ВН2 + НО2

Ответ: OB = 10,625

Задача 8: в ромб вписана окружность радиуса R. Найти площадь ромба, если его большая диагональ в 4 раза больше радиуса вписанной окружности.

Дано: ромб, радиус вписанной окружности – R, BD r в 4 раза

Найти:

1. Пусть OE = R, BD = 4OE = 4R

2.

3.

4.

Ответ:

Задача 9: найдите площадь равнобедренной трапеции, описанной около окружности с радиусом 4, если известно, что боковая сторона трапеции равна 10.

Дано: ABCD – равнобедренная трапеция, r = 4, AB = 10

Найти:

1. AB = CD = 10 по условию

2. AB + CD = AD + BC по свойству вписанной окружности

3. AD + BC = 10 + 10 = 20

4. FE = 2r = 2 · 4 = 8

5.

Ответ:

Задача 10: внутри правильного треугольника со стороной a расположены три равные окружности, каждая из которых касается двух сторон треугольника и двух других окружностей. Найти площадь части треугольника, расположенной вне этих окружностей.

1. Пусть AB = BC = AC = a.

2. Обозначим O1E = O1K = ED = r, тогда AD = AE + ED = AE + r = .

3. AO1 – биссектриса угла A, следовательно, ﮮ O1AE = 30˚ и в прямоугольном ∆AO1E имеем AO1 = 2O1E = 2r и AE ===. Тогда AE + r = == , откуда .

4.

Ответ:

Задача 11: вся дуга окружности радиуса R разделена на 4 большие и 4 малые части, которые чередуются одна за другой. Большая часть в два раза длиннее малой. Определить площадь восьмиугольника, вершинами которого являются точки деления дуги окружности.

1. Пусть ﮮAOB = 2x, ﮮBOC = x, тогда по условию 8x + 4x = 360°, x = 30°, 2x = 60°, ﮮAOB = 60°, ﮮBOC = 30°

2.

3.

4.

Ответ:

Задача 12: стороны треугольника равны 12 м, 16 м и 20 м. Найдите го высоту, проведенную из вершины большего угла.

1. 202 = 122 + 162

400 = 400 верно, следовательно, ∆ АВС – прямоугольный (по теореме, обратной теореме Пифагора)

2.

3.

Задача 13: в прямоугольный треугольник вписан квадрат, имеющий с ним общий угол. Найдите площадь квадрата, если катеты треугольника равны 10 м и 15 м.

Дано: ∆ ABC – прямоугольный, AC = 15, CB = 10

Найти:

∆ ACB (ﮮ A – общий, ﮮ ADE = ﮮ ACB = 90°)

2. Пусть DE = DC = X, тогда AD = 15 – X

3.

15 · X = 150 – 10 · X

4. S кв. = 6 · 6 = 36

Задача 14: основания трапеции равны 10 м и 31 м, а боковые стороны – 20 м и 13 м. Найдите высоту трапеции.

2. Пусть BH = CK = x, AH=y, тогда KD = 21 – y

3. По теореме Пифагора:

x2 + y2 = 132

x2 + (21 – y)2 = 202

x2 + 441 – 42y + y2 = 400

4. По теореме Пифагора:

В процессе работы я расширил знания по теме «Вписанные и описанные окружности в треугольниках и четырехугольниках», научился решать задачи, казавшиеся ранее недоступными, систематизировал знания по этой теме, и закрепил методы решения этих задач на практике.

Так как геометрические задачи этой темы включаются во вторую часть экзаменационной работы ЕГЭ за курс средней школы, то в дальнейшем мне будет намного легче справиться с ними на ЕГЭ.

1. «Единый государственный экзамен 2006. Математика. Учебно-тренировочные материалы для подготовки учащихся/ Рособрнадзор, ИСОП – М.: Интеллект-Центр, 2006»

2. «Решение основных конкурсных задач по математике сборника под редакцией »

3. , , «Геометрия, 7 – 9: учебник для общеобразовательных учреждений»

📸 Видео

7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Всякий равносторонний треугольник является остроугольным. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

7 класс, 32 урок, Остроугольный, прямоугольный и тупоугольный треугольникиСкачать

Как построить равнобедренный или равносторонний треугольник по клеткам.Скачать

Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

ОГЭ Р-2 номер 16Скачать

Всякий равнобедренный треугольник является остроугольным. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

№118. На основании ВС равнобедренного треугольника ABC отмечены точки М и N так, что BM=CN. ДокажитеСкачать

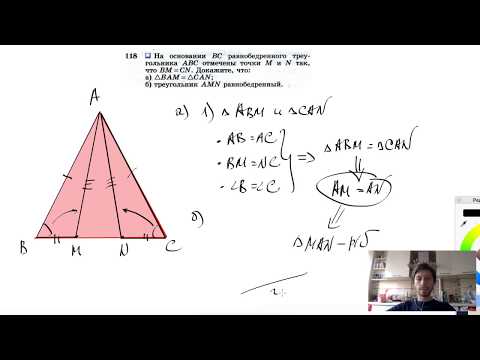
ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Равнобедренный треугольникСкачать

Центр описанной окружности равнобедренного треугольника ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

№703. В окружность вписан равнобедренный треугольник ABC с основанием ВС. Найдите углы треугольникаСкачать