Осевое сечение конуса равносторонний треугольник

Так как все образующие конуса равны, то его осевым сечением является равнобедренный треугольник, боковыми сторонами которого являются образующие конуса, а основанием — диаметр конуса. При этом все осевые сечения конуса — равные равнобедренные треугольники . На рисунке 168 осевым сечением конуса является треугольник ABP ( АР = ВР ). Угол АPВ называют углом при вершине осевого сечения конуса .

Конус, в осевом сечении которого правильный треугольник, называется равносторонним конусом.

Если секущая плоскость проходит через вершину конуса, пересекает конус, но не проходит через его ось, то в сечении конуса также получается равнобедренный треугольник (см. рис. 168: △ DCP ).

Так как конус — тело вращения, то любое сечение конуса плоскостью, перпендикулярной его оси (т. е. параллельной основанию конуса), есть круг, а сечение боковой поверхности конуса такой плоскостью — окружность этого круга; центром круга (окружности) является точка пересечения оси конуса и секущей плоскости (рис. 169).

Если секущая плоскость не параллельна плоскости основания конуса и не пересекает основание, то сечением боковой поверхности конуса такой плоскостью является эллипс (рис. 170). Поэтому эллипс называют коническим сечением .

Если сечением цилиндрической поверхности плоскостью может быть либо окружность, либо эллипс, либо две параллельные прямые, то сечением конической поверхности плоскостью может быть либо окружность (секущая плоскость перпендикулярна оси конической поверхности вращения и не проходит через её вершину, рис. 171, a ), либо эллипс (секущая плоскость не перпендикулярна оси конической поверхности и пересекает все её образующие, рис. 171, б ), либо парабола (секущая плоскость параллельна только одной образующей конической поверхности, рис. 171, в ), либо гипербола (секущая плоскость параллельна оси конической поверхности, рис. 171, г ), либо пара пересекающихся прямых (секущая плоскость проходит через вершину конической поверхности, рис. 171, д ). Поэтому невырожденные кривые второго порядка — окружность, эллипс, параболу и гиперболу называют коническими сечениями или коротко — кониками .

О конических сечениях можно прочитать в очерках «Элементарная геометрия», «Проективная геометрия» в конце этой книги.

 ЗАДАЧА (3.047). Высота конуса равна радиусу R его основания. Через вершину конуса проведена плоскость, отсекающая от окружности основания дугу: а) в 60 ° ; б) в 90 ° . Найти площадь сечения.

Решени е. Рассмотрим случай а). Пусть плоскость α пересекает поверхность конуса с вершиной Р по образующим РА и РВ (рис. 172); △ АВР — искомое сечение. Найдём площадь этого сечения.

Хорда АВ окружности основания стягивает дугу в 60 ° , значит, △ AOB — правильный и АВ = R .

Если точка С — середина стороны АB, то отрезок PC — высота треугольника АВР. Поэтому S △ ABP = АВ • РC. Имеем: ОР = R (по условию); в △ A OB : ОС = ; в △ ОСР : CP = = .

Тогда S △ ABP = АВ • РС = .

Ответ: а) .

18.3. Касательная плоскость к конусу

Определение. Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса перпендикулярно осевому сечению, проведённому через эту образующую.

Говорят, что плоскость α касается конуса по образующей РА (рис. 173): каждая точка образующей РА является точкой касания плоскости α и данного конуса.

Через любую точку боковой поверхности конуса проходит только одна его образующая. Через эту образующую можно провести только одно осевое сечение и только одну плоскость, перпендикулярную плоскости этого осевого сечения. Следовательно, через каждую точку боковой поверхности конуса можно провести лишь одну плоскость, касательную к данному конусу в этой точке.

18.4. Изображение конуса

Для изображения конуса достаточно построить: 1) эллипс, изображающий окружность основания конуса (рис. 174); 2) центр О этого эллипса; 3) отрезок ОР, изображающий высоту конуса; 4) касательные прямые РА и PB из точки Р к эллипсу (их проводят с помощью линейки на глаз).

Для достижения наглядности изображения невидимые линии изображают штрихами.

Необходимо заметить, что отрезок АВ, соединяющий точки касания образующих и окружности основания конуса, ни в коем случае не является диаметром основания конуса, т. е. этот отрезок не содержит центра О эллипса. Следовательно, △ АBP — не осевое сечение конуса. Осевым сечением конуса является △ ACP, где отрезок AC проходит через точку О, но образующая PC не является касательной к окружности основания.

18.5. Развёртка и площадь поверхности конуса

Пусть l — длина образующей, R — радиус основания конуса с вершиной Р .

Поверхность конуса состоит из боковой поверхности конуса и его основания. Если эту поверхность разрезать по одной из образующих, например по образующей PA (рис. 175), и по окружности основания, затем боковую поверхность конуса развернуть на плоскости (рис. 176, a ), то получим развёртку поверхности конуса (рис. 176, б ), состоящую из: а) кругового сектора, радиус которого равен образующей l конуса, а длина дуги сектора равна длине окружности основания конуса; б) круга, радиус которого равен радиусу R основания конуса. Угол сектора развёртки боковой поверхности конуса называют углом развёртки конуса ; его численная величина равна отношению длины окружности основания конуса к его образующей (радиусу сектора развёртки):

α = .

За площадь боковой поверхности конуса принимается площадь её развёртки. Выразим площадь боковой поверхности конуса через длину l его образующей и радиус R основания.

Площадь боковой поверхности — площадь кругового сектора радиуса длины l — вычисляется по формуле

S бок = α • l 2 , (1)

где α — величина угла (в радианах) сектора — развёртки. Учитывая, что α = , получаем:

Таким образом, доказана следующая теорема.

Теорема 27. Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую. ▼

Площадь полной поверхности конуса равна сумме площадей его боковой поверхности и основания, т. е.

S кон = π Rl + π R 2 . (3)

Следствие. Пусть конус образован вращением пря м оугольного треугольника ABC вокруг катета АС (рис. 177). Тогда S бок = π • BC • АВ. Если D — середина отрезка АВ, то AB = 2 AD, поэтому

S бок = 2 π ВС • AD. (4)

Проведём DE ⟂ АB ( E ∈ l = AС ) . Из подобия прямоугольных треугольников ADE и ACB (у них общий угол А ) имеем

= ⇒ BC • AD = DE • АС. (5)

Тогда соотношение (4) принимает вид

S бок = (2 π • DE ) • AC, (6)

т. е. площадь боковой поверхности конуса равна произведению высоты конуса на длину окружности, радиус которой равен длине серединного перпендикуляра, проведённого из точки на оси конуса к его образующей.

Это следствие будет использовано в п. 19.7.

18.6. Свойства параллельных сечений конуса

Теоремa 28. Если конус пересечён плоскостью, параллельной основанию, то: 1) все образующие и высота конуса делятся этой плоскостью на пропорциональные части; 2) в сечении получается круг; 3) площади сечения и основания относятся, как квадраты их расстояний от вершины.

Доказательств о. 1) Пусть конус с вершиной Р и основанием F пересечён плоскостью α , параллельной плоскости β основания конуса и расположенной между Р и β (рис. 178).

Проведём высоту РО конуса, где точка О — центр круга F. Так как РО ⟂ β , α || β , то α ⟂ РО. Значит, в сечении конуса плоскостью α получается круг с центром в точке O 1 = α ∩ РО. Обозначим этот круг F 1 .

Рассмотрим гомотетию с центром P, при которой плоскость β основания данного конуса отображается на параллельную ей плоскость α (при гомотетии плоскость, не проходящая через центр гомотетии, отображается на параллельную ей плоскость).

Так как при гомотетии её центр является неподвижной точкой, прямая, проходящая через центр гомотетии, отображается на себя, а пересечение двух фигур — на пересечение их образов, то гомотетия отображает основание F конуса на его параллельное сечение — круг F 1 , при этом центр О основания отображается на центр О 1 круга F 1 (почему?). Кроме того, если РХ — произвольная образующая конуса, где Х — точка окружности основания, то при гомотетии точка X отображается на точку X 1 = РX ∩ α . Учитывая, что отношение длин гомотетичных отрезков равно коэффициенту гомотетии, получаем:

= = k, (*)

где k — коэффициент гомотетии , т. е. параллельное сечение конуса делит его образующие и высоту на пропорциональные части.

А поскольку гомотетия является подобием, то круг F 1 , являющийся параллельным сечением конуса, подобен его основанию.

Вследствие того что отношение площадей гомотетичных фигур равно квадрату коэффициента гомотетии и k = PO 1 : Р О , где РO 1 и PO — расстояния соответственно параллельного сечения и основания пирамиды от её вершины, то

S сечен : S основ = k 2 = : PO 2 .

18.7. Вписанные в конус и описанные около конуса пирамиды

Определение. Пирамида называется вписанной в конус, если у них вершина общая, а основание пирамиды вписано в основание конуса. В этом случае конус называется описанным около пирамиды.

Для построения изображения правильной пирамиды, вписанной в конус:

— строят изображение основания пирамиды — правильного многоугольника, вписанного в основание конуса;

— соединяют отрезками прямых вершину конуса с вершинами построенного многоугольника;

— выделяют видимые и невидимые (штрихами) линии изображаемых фигур.

На рисунках 179—182 изображена вписанная в конус пирамида, в основаниях которой лежит:

— прямоугольный треугольник (см. рис. 179);

Видео:№550. Осевое сечение конуса — прямоугольный треугольник. Найдите площадь этого сечения, еслиСкачать

Осевое сечение конуса — равносторонний треугольник со стороной 12 см?

Геометрия | 5 — 9 классы

Осевое сечение конуса — равносторонний треугольник со стороной 12 см.

Найти объем конуса.

ВН — высота, атакжемедиана.

V = 1 / 3 * П * R ^ 2 * h = 1 / 3 * П * 36 * 6√3 = 72√3 * П

(Если нужнополностьючисловоезначение, тоизвлекикотенькалькулятором, аП = 3, 14).

Видео:№551. Осевое сечение конуса — правильный треугольник со стороной 2г. Найдите площадь сечения,Скачать

В конус вписан шар объемом 2?

В конус вписан шар объемом 2.

Найдите объем конуса, если его осевое сечение является равносторонним треугольником.

Видео:Конус. 11 класс.Скачать

Осевое сечение конуса — правильный треугольник со стороной 5, найдите объем конуса?

Осевое сечение конуса — правильный треугольник со стороной 5, найдите объем конуса.

Видео:Геометрия 11 класс (Урок№7 - Конус.)Скачать

Осевое сечение конуса — правильный треугольник со стороной 6?

Осевое сечение конуса — правильный треугольник со стороной 6.

Найти объем конуса помогите пожалуйста !

С решением желательно.

Видео:Геометрия Осевым сечением конуса является прямоугольный треугольник с гипотенузой равной аСкачать

Осевое сечение конуса — равностороний треугольник со стороной 2 см?

Осевое сечение конуса — равностороний треугольник со стороной 2 см.

Найдите объем и площадь поверхности конуса.

Видео:сечение конусаСкачать

Осевое сечение конуса равносторонний треугольник со стороной 6см найдите обьем?

Осевое сечение конуса равносторонний треугольник со стороной 6см найдите обьем.

Видео:Решение задач на конусСкачать

Объем конуса 9корней из 3 пи см3?

Объем конуса 9корней из 3 пи см3.

Найдите высоту конуса, если его осевое сечение — равносторонний треугольник.

Видео:№554. Образующая конуса равна l, а радиус основания равен r. Найдите площадь сечения, проходящегоСкачать

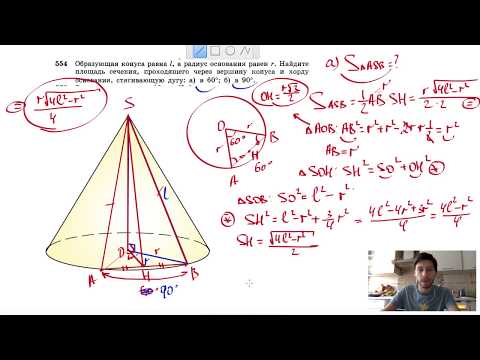
Осевое сечение конуса есть равносторонний треугольник со стороной а ?

Осевое сечение конуса есть равносторонний треугольник со стороной а .

Найдите площадь боковой поверхности этого конуса .

Видео:Усеченный конус. 11 класс.Скачать

Найдите объем конуса, осевым сечением которого является равносторонний треугольник со стороной 12 см?

Найдите объем конуса, осевым сечением которого является равносторонний треугольник со стороной 12 см.

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Найти объем равностороннего конуса, сторона осевого сечения равна 10см?

Найти объем равностороннего конуса, сторона осевого сечения равна 10см.

Видео:11 класс, 16 урок, Понятие конусаСкачать

СРОЧНЯК?

Осевое сечение конуса есть равносторонний треугольник со стороной а.

Найдите площадь боковой поверхности этого конуса.

На этой странице сайта, в категории Геометрия размещен ответ на вопрос Осевое сечение конуса — равносторонний треугольник со стороной 12 см?. По уровню сложности вопрос рассчитан на учащихся 5 — 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

Значит угол B = углуD = 120 как противоположные в параллелограмме угол D находится между сторонами AD и DC значит можно воспользоваться формулою площади S = AD * DC * sinD = 12 * 32 / кор3 * кор3 / 2 = 192 см ^ 2 что такое кор3 / 2 это синус120.

C = 29 B = 122 D = 122 Вроде так.

В = 122° С = 29° D = 122° вот.

Решение дано на фото.

1. M и N — точки принадлежат одной плоскости АВС. Проводим NM до пересечения с продолжением CА в точке Р. 2. Р и К — точки принадлежат одной плоскости, содержащей грань АА1С1С. Проводим РК до пересечения с продолжением CС1 в точке Т и получаем точ..

В равнобедренном треугольнике.

Вертикаль опущенная из Е на основание разбивает треугольник FED на два, каждый из которых подобен треугольникам, отсекаемых вертикалями из вершин В и С. Размер этих (маленьких) треугольников в 2 раза меньше подобных, значит общее основание больших т..

Решение смотри в файле.

Abcd параллелограмм, ab = 5cm значит cd = 5сm p = 2(a + b) P = 290 значит 290 : 2 = 145 145 : 2 = 72, 5 следовательно bc = 72. 5 ad = 72, 5.

Видео:Тема 6. Конус. Осевое сечение конуса. Развертка боковой поверхности конуса. Площадь боковой и полнойСкачать

Что такое сечение конуса? Как найти площадь осевого сечения конуса

Одной из фигур, которая встречается при решении геометрических задач в пространстве, является конус. Он, в отличие от многогранников, относится к классу фигур вращения. Рассмотрим в статье, что понимают под ним в геометрии, и исследуем характеристики различных сечений конуса.

Видео:Сечение конусаСкачать

Конус в геометрии

Предположим, что имеется некоторая кривая на плоскости. Это может быть парабола, окружность, эллипс и так далее. Возьмем точку, которая указанной плоскости не принадлежит, и соединим с ней все точки кривой. Образованная поверхность называется конической или просто конусом.

Вам будет интересно: Что такое конус: определение. Основание, вершина, высота конуса

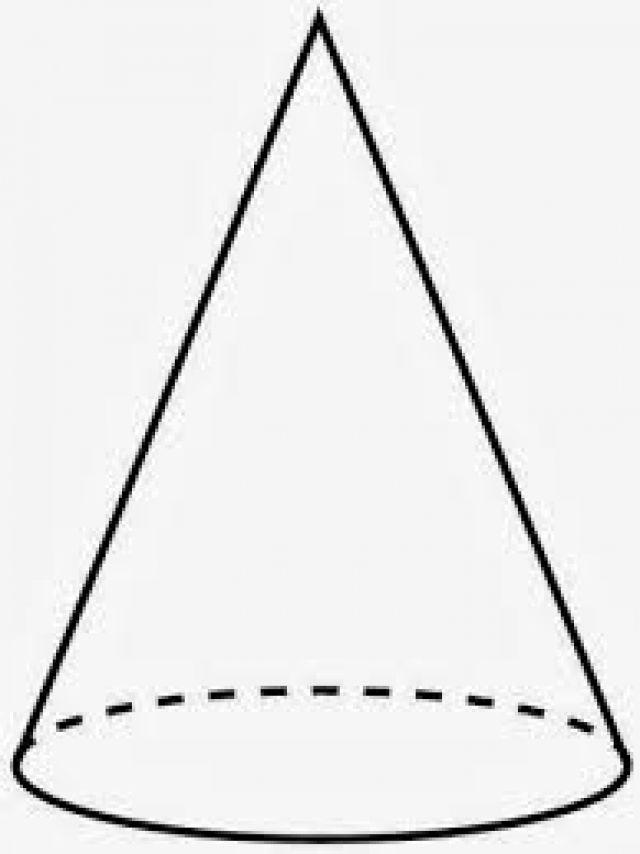
Если исходная кривая является замкнутой, тогда коническую поверхность можно заполнить веществом. Полученная таким образом фигура является объемным телом. Она также называется конусом. Несколько конусов, изготовленных из бумаги, показаны ниже на рисунке.

Коническая поверхность встречается в обычной жизни. Например, этой формой обладает мороженое-рожок или дорожный полосатый конус, который призван привлечь внимание водителей и пешеходов.

Видео:2 6 1 сечение конуса плоскостьюСкачать

Виды конусов

Вам будет интересно: Подберем рифму к слову «капля»

Как можно догадаться, рассматриваемые фигуры друг от друга отличаются типом кривой, на которой они образованы. Например, существует круглый конус или эллиптический. Данная кривая называется основанием фигуры. Однако форма основания — это не единственная особенность, позволяющая классифицировать конусы.

Второй важной их характеристикой является положение высоты относительно основания. Высотой конуса называется прямой отрезок, который опущен из вершины фигуры к плоскости основания и перпендикулярен этой плоскости. Если высота пересекает в геометрическом центре основание (например, в центре круга), то конус будет прямым, если перпендикулярный отрезок падает в любую другую точку основания или за его пределы, то фигура будет наклонной.

Далее в статье будем рассматривать только круглый прямой конус как яркий представитель рассматриваемого класса фигур.

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Геометрические названия элементов конуса

Выше было сказано, что конус имеет основание. Оно ограничено окружностью, которая называется направляющей конуса. Отрезки, соединяющие направляющую с точкой, не лежащей в плоскости основания, называются образующими. Совокупность всех точек образующих называется конической или боковой поверхностью фигуры. Для круглого прямого конуса все образующие имеют одинаковую длину.

Вам будет интересно: Абашевская культура бронзового века: локализация, археологические находки

Точка, где образующие пересекаются, называется вершиной фигуры. В отличие от многогранников, конус имеет единственную вершину и не имеет ни одной грани.

Прямая линия, проходящая через вершину фигуры и центр круга, называется осью. Ось содержит в себе высоту прямого конуса, поэтому она с плоскостью основания образует прямой угол. Эта информация важна при вычислении площади осевого сечения конуса.

Видео:№562. Угол между образующей и осью конуса равен 45°, образующая равна 6,5 см. НайдитеСкачать

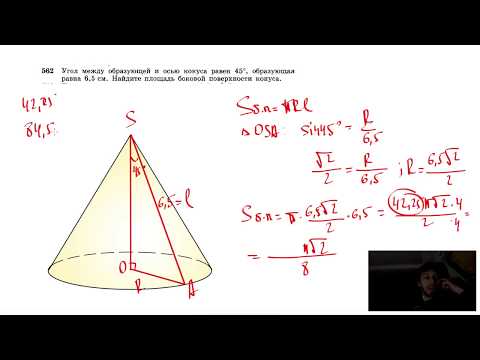
Круглый прямой конус — фигура вращения

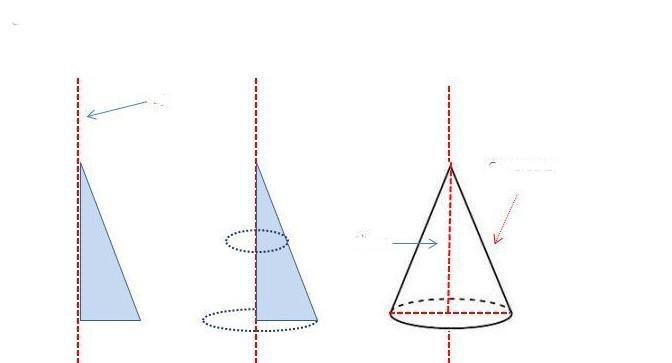
Рассматриваемый конус является достаточно симметричной фигурой, которую можно получить в результате вращения треугольника. Предположим, что имеется треугольник с прямым углом. Чтобы получить конус, достаточно вращать этот треугольник вокруг одного из катетов так, как показано на рисунке ниже.

Видно, что ось вращения является осью конуса. Один из катетов будет равен высоте фигуры, а второй катет станет радиусом основания. Гипотенуза треугольника в результате вращения опишет коническую поверхность. Она будет образующей конуса.

Указанный способ получения круглого прямого конуса удобно использовать для изучения математической связи между линейными параметрами фигуры: высоты h, радиуса круглого основания r и направляющей g. Соответствующая формула следует из свойств прямоугольного треугольника. Она приведена ниже:

Поскольку мы имеем одно уравнение и три переменных, то это означает, что для однозначного задания параметров круглого конуса необходимо знать две любые величины.

Видео:№555. Высота конуса равна 10 см. Найдите площадь сечения, проходящего через вершину конусаСкачать

Сечения конуса плоскостью, которая не содержит вершину фигуры

Вопрос построения сечений фигуры не является тривиальным. Дело в том, что форма сечения конуса поверхностью зависит от взаимного расположения фигуры и секущей.

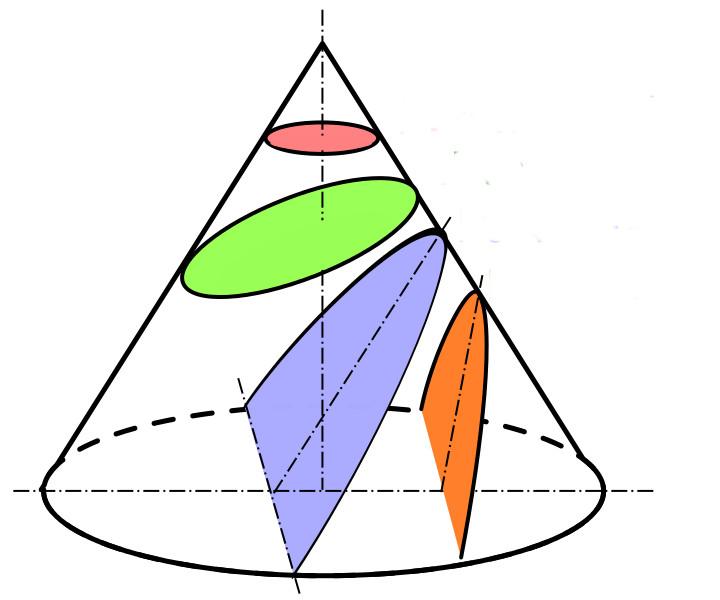
Предположим, что мы пересекаем конус плоскостью. Какое сечение получится в результате этой геометрической операции? Варианты формы сечения показаны на рисунке ниже.

Розовое сечение является кругом. Оно образовано в результате пересечения фигуры плоскостью, которая параллельна основанию конуса. Это сечения перпендикулярно оси фигуры. Образованная выше секущей плоскости фигура представляет собой конус, подобный исходному, но имеющий круг меньшего размера в основании.

Зеленое сечение — это эллипс. Он получается, если секущая плоскость не параллельна основанию, однако она пересекает только боковую поверхность конуса. Отсеченная выше плоскости фигура называется эллиптическим наклонным конусом.

Синее и оранжевое сечения имеют форму параболы и гиперболы, соответственно. Как видно из рисунка, они получаются, если секущая плоскость одновременно пересекает боковую поверхность и основание фигуры.

Для определения площадей сечений конуса, которые были рассмотрены, необходимо использовать формулы для соответствующей фигуры на плоскости. Например, для круга это умноженное на квадрат радиуса число Пи, а для эллипса — это произведение Пи на длину малой и большой полуосей:

Видео:Геометрия. 11 класс. Конус и его элементы. Развертка, площадь боковой и полной поверхности конусаСкачать

Сечения, содержащие вершину конуса

Теперь рассмотрим варианты сечений, которые возникают, если секущая плоскость будет проходить через вершину конуса. Возможны три случая:

Осевое сечение. Оно образуется, когда плоскость содержит не только вершину фигуры, но и всю ее ось. При этом плоскость будет перпендикулярна круглому основанию и разделит конус на две равные части.

Очевидно, что площади первых двух видов сечений равны нулю. Что касается площади сечения конуса для 3-го вида, то этот вопрос подробнее рассматривается в следующем пункте.

Видео:Усеченный конус. Практическая часть. 11 класс.Скачать

Осевое сечение

Выше отмечалось, что осевым сечением конуса называется фигура, образованная при пересечении конуса плоскостью, проходящей через его ось. Несложно догадаться, что это сечение будет представлять фигуру, показанную на рисунке ниже.

Это равнобедренный треугольник. Вершина осевого сечения конуса — это вершина этого треугольника, образованная пересечением одинаковых сторон. Последние равны длине образующей конуса. Основание треугольника — это диаметр основания конуса.

Вычисление площади осевого сечения конуса сводится к нахождению площади полученного треугольника. Если изначально известны радиус основания r и высота h конуса, тогда площадь S рассматриваемого сечения будет равна:

Это выражение является следствием применения стандартной формулы для площади треугольника (половина произведения высоты на основание).

Отметим, что если образующая конуса будет равна диаметру его круглого основания, то осевое сечение конуса — треугольник равносторонний.

Треугольное сечение образуется тогда, когда секущая плоскость перпендикулярна основанию конуса и проходит через его ось. Любая другая плоскость, параллельная названной, даст в сечении гиперболу. Однако если плоскость содержит вершину конуса и пересекает его основание не через диаметр, то полученное сечение тоже будет равнобедренным треугольником.

Видео:Понятие конуса. Видеоурок по геометрии 11 классСкачать

Задача на определение линейных параметров конуса

Покажем, как пользоваться записанной для площади осевого сечения формулой для решения геометрической задачи.

Известно, что площадь осевого сечения конуса равна 100 см2. Полученный в сечение треугольник является равносторонним. Чему равны высота конуса и радиус его основания?

Поскольку треугольник равносторонний, то его высота h связана с длиной стороны a следующим соотношением:

Учитывая, что сторона треугольника в два раза больше радиуса основания конуса, и подставляя это выражение в формулу для площади сечения, получаем:

Тогда высота конуса равна:

Остается подставить значение площади из условия задачи и получить ответ:

r = √(100/√3) ≈ 7,60 см;

h = √(√3*100) ≈ 13,16 см.

В каких областях важно знать параметры рассмотренных сечений?

Изучение различных типов сечений конуса представляет не только теоретический интерес, но также имеет практическое приложение.

Во-первых, следует отметить область аэродинамики, где с помощью конических сечений удается создавать идеальные гладкие формы твердых тел.

Во-вторых, конические сечения являются траекториями, по которым движутся космические объекты в гравитационных полях. Какой конкретно вид сечения представляет траектория движения космических тел системы, определяется соотношением их масс, абсолютных скоростей и расстояний между ними.