Как построить диметрию треугольника

Во многих случаях при выполнении технических чертежей оказывается полезным наряду изображением предметов в системе ортогональных проекций иметь более наглядные изображения. Для построения таких изображений применяются проекции, называемые аксонометрическими .

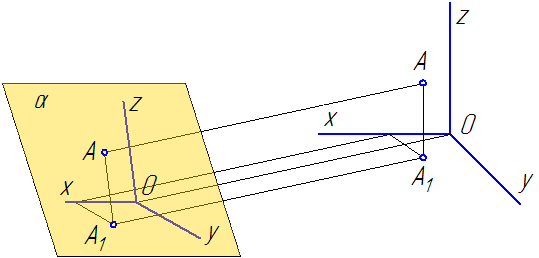
Способ аксонометрического проецирования состоит в том, что данный предмет вместе с осями прямоугольных координат, к которым эта система относится в пространстве, параллельно проецируется на некоторую плоскость α (Рисунок 4.1).

Рисунок 4.1p/

Направление проецирования S определяет положение аксонометрических осей на плоскости проекций α, а также коэффициенты искажения по ним. При этом необходимо обеспечить наглядность изображения и возможность производить определения положений и размеров предмета.
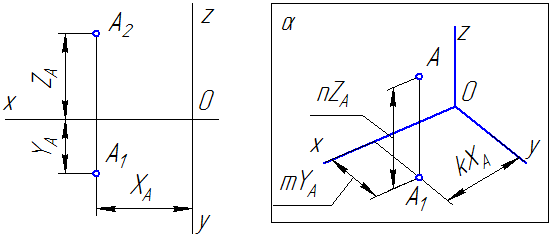
В качестве примера на Рисунке 4.2 показано построение аксонометрической проекции точки А по ее ортогональным проекциям.

Рисунок 4.2

Здесь буквами k, m, n обозначены коэффициенты искажения по осям OX, OY и OZ соответственно. Если все три коэффициента равны между собой, то аксонометрическая проекция называется изометрической, если равны между собой только два коэффициента, то проекция называется диметрической, если же k≠m≠n, то проекция называется триметрической.
Если направление проецирования S перпендикулярно плоскости проекций α, то аксонометрическая проекция носит названия прямоугольной. В противном случае, аксонометрическая проекция называется косоугольной.
ГОСТ 2.317-2011 устанавливает следующие прямоугольные и косоугольные аксонометрические проекции:

• прямоугольные изометрические и диметрические;
• косоугольные фронтально изометрические, горизонтально изометрические и фронтально диметрические;

Ниже приводятся параметры только трех наиболее часто применяемых на практике аксонометрических проекций.
Каждая такая проекция определяется положением осей, коэффициентами искажения по ним, размерами и направлениями осей эллипсов, расположенных в плоскостях, параллельных координатным плоскостям. Для упрощения геометрических построений коэффициенты искажения по осям, как правило, округляются.

Видео:Черчение. 8 класс. Мазаева И.М. Изометрия и ДиметрияСкачать

4.1. Прямоугольные проекции

4.1.1. Изометрическая проекция

Направление аксонометрических осей приведено на Рисунке 4.3.

Рисунок 4.3 – Аксонометрические оси в прямоугольной изометрической проекции

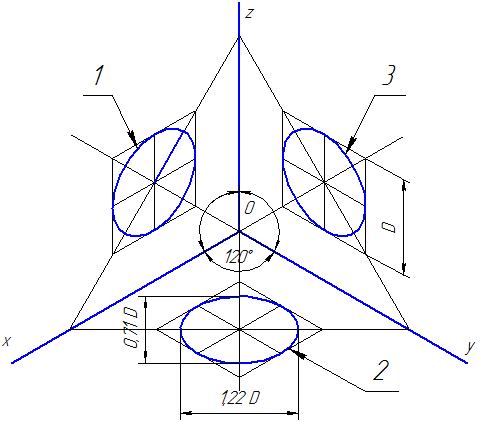
Действительные коэффициенты искажения по осям OX, OY и OZ равны 0,82. Но с такими значениями коэффициентов искажения работать не удобно, поэтому, на практике, используются приведенные коэффициенты искажений. Эта проекция обычно выполняется без искажения, поэтому, приведенные коэффициенты искажений принимается k = m = n =1. Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются в эллипсы, большая ось которых равна 1,22, а малая – 0,71 диаметра образующей окружности D.

Большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.

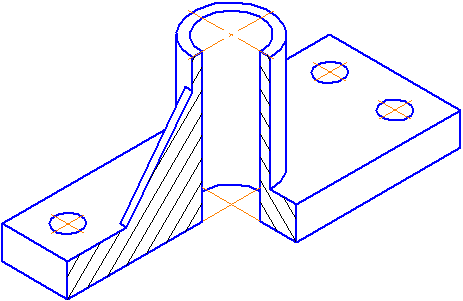
Пример выполнения изометрической проекции условной детали с вырезом приводится на Рисунке 4.4.

Рисунок 4.4 – Изображение детали в прямоугольной изометрической проекции

4.1.2. Диметрическая проекция

Положение аксонометрических осей проводится на Рисунке 4.5.

Для построения угла, приблизительно равного 7º10´, строится прямоугольный треугольник, катеты которого составляют одну и восемь единиц длины; для построения угла, приблизительно равного 41º25´ — катеты треугольника, соответственно, равны семи и восьми единицам длины.

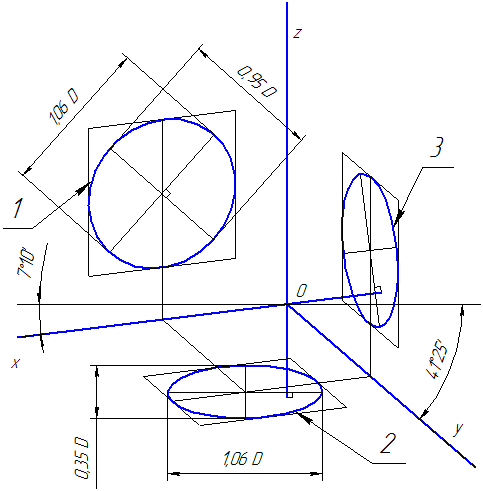
Коэффициенты искажения по осям ОХ и OZ k=n=0,94 а по оси OY – m=0,47. При округлении этих параметров принимается k=n=1 и m=0,5. В этом случае размеры осей эллипсов будут: большая ось эллипса 1 равна 0,95D и эллипсов 2 и 3 – 0,35D (D – диаметр окружности). На Рисунке 4.5 большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.

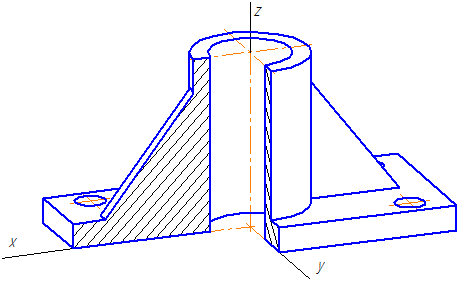
Пример прямоугольной диметрической проекции условной детали с вырезом приводится на Рисунке 4.6.

Рисунок 4.5 – Аксонометрические оси в прямоугольной диметрической проекции

Рисунок 4.6 – Изображение детали в прямоугольной диметрической проекции

Видео:Построение треугольника в трёх проекцияхСкачать

4.2 Косоугольные проекции

4.2.1 Фронтальная диметрическая проекция

Положение аксонометрических осей приведено на Рисунке 4.7. Допускается применять фронтальные диметрические проекции с углом наклона к оси OY, равным 30 0 и 60 0 .

Коэффициент искажения по оси OY равен m=0,5 а по осям OX и OZ — k=n=1.

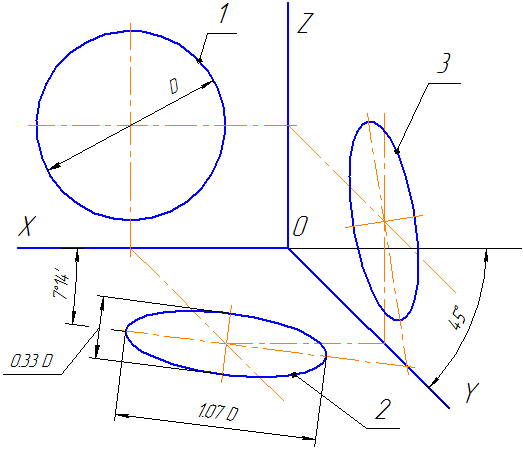
Рисунок 4.7 – Аксонометрические оси в косоугольной фронтальной диметрической проекции

Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на плоскость XOZ без искажения. Большие оси эллипсов 2 и 3 равны 1,07D, а малая ось – 0,33D (D — диаметр окружности). Большая ось эллипса 2 составляет с осью ОХ угол 7º 14´, а большая ось эллипса 3 составляет такой же угол с осью OZ.

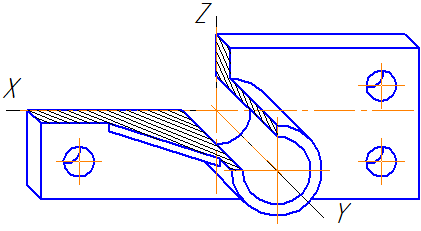
Пример аксонометрической проекции условной детали с вырезом приводится на Рисунке 4.8.

Как видно из рисунка, данная деталь располагается таким образом, чтобы её окружности проецировались на плоскость XОZ без искажения.

Рисунок 4.8 – Изображение детали в косоугольной фронтальной диметрической проекции

Видео:Как начертить диметрию. Уроки черчения.Скачать

4.3 Построение эллипса

4.3.1 Построения эллипса по двум осям

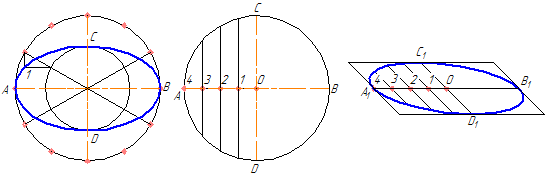
На данных осях эллипса АВ и СD строятся как на диаметрах две концентрические окружности (Рисунок 4.9, а).

Одна из этих окружностей делится на несколько равных (или неравных) частей.

Через точки деления и центр эллипса проводятся радиусы, которые делят также вторую окружность. Затем через точки деления большой окружности проводятся прямые, параллельные линии АВ.

Точки пересечения соответствующих прямых и будут точками, принадлежащими эллипсу. На Рисунке 4.9, а показана лишь одна искомая точка 1.

а б в
Рисунок 4.9 – Построение эллипса по двум осям (а), по хордам (б)

4.3.2 Построение эллипса по хордам

Диаметр окружности АВ делится на несколько равных частей, на рисунке 4.9,б их 4. Через точки 1-3 проводятся хорды параллельно диаметру CD. В любой аксонометрической проекции (например, в косоугольной диметрической) изображаются эти же диаметры с учетом коэффициента искажения. Так на Рисунке 4.9,б А₁В₁=АВ и С₁ D₁ = 0,5CD. Диаметр А ₁В₁ делится на то же число равных частей, что и диаметр АВ, через полученные точки 1-3 проводятся отрезки, равные соответственным хордам, умноженным на коэффициент искажение (в нашем случае – 0,5).

4.4 Штриховка сечений

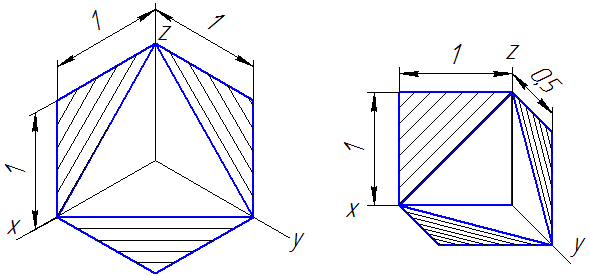
Линии штриховки сечений (разрезов) в аксонометрических проекциях наносятся параллельно одной из диагоналей квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям (Рисунок 4.10: а – штриховка в прямоугольной изометрии; б – штриховка в косоугольной фронтальной диметрии).

а б
Рисунок 4.10 – Примеры штриховки в аксонометрических проекциях

Видео:Построение окружности в диметрииСкачать

Аксонометрическое проецирование

Содержание:

Аксонометрическое проецирование — это способ аксонометрического проецирования состоит в том, что данная фигура вместе с осями прямоугольных координат, к которым она отнесена в пространстве, параллельно проецируется на некоторую плоскость, принятую за плоскость аксонометрических проекций (эту плоскость называют также картинной плоскостью).

Видео:Построение эллипса по восьми точкам в прямоугольной диметрииСкачать

Виды аксонометрического проецирования

Метод ортогонального проецирования на взаимно перпендикулярные плоскости проекций П1, П2, П3 имеет существенный недостаток, состоящий в том, что представление пространственного образа предмета возможно только при условии одновременного изучения по крайней мере двух его проекций. Способ аксонометрического проецирования устраняет обозначенный недостаток, давая возможность одновременно видеть изображение предмета с двух или трёх сторон.

Аксонометрическое проецирование (от греческого άξονας – ось и µετρο – мера) – способ изображения геометрических предметов при условии параллельного проецирования на плоскость общего положения. Эта плоскость называется картинной.

При аксонометрическом проецировании предмет проецируется на картинную плоскость вместе с осями x, y, z ортогональной системы координат. Последние проецируются на картинную плоскость в оси аксонометрического проецирования (рис. 6.1 а).

Способ аксонометрического проецирования

Единичные отрезки ОХ, ОY, OZ проецируются на в отрезки длина которых меньше единицы, поэтому аксонометрическая проекция любого объекта является искажённой по трём координатным осям. Степень уменьшения характеризуется коэффициентами искажения числовые значения которых равны длинам проекций единичных отрезков ОХ, ОY, OZ на картинную плоскость. Коэффициенты являются основными параметрами аксонометрического проецирования. Они равны косинусам углов α, β, γ наклона осей х, у, z до плоскости . Кроме того, коэффициенты искажения связаны между собой соотношением

где φ – угол аксонометрического проецирования.

Углы наклона осей к горизонту (рис. 6.1 б) зависят от угла φ и коэффициентов (см. п. 6.2 – 6.3).

Виды аксонометрического проецирования обусловлены числовым значением угла φ проецирования и соотношениями коэффициентов искажения (рис. 6.2).

Классификация аксонометрических проекций

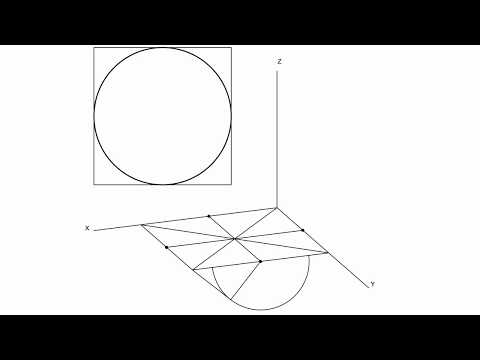
На рис. 6.1 б показан способ построения аксонометрической проекции точки А с координатами х, у, z. Для её построения из начала отсчёта вдоль оси откладывается отрезок длиной Из полученной точки параллельно оси проводится отрезок длиной Из полученной точки проводится вертикальный отрезок длиной Полученная точка — искомая аксонометрическая проекция точки А.

Со всего множества аксонометрических проекций на практике применяются преимущественно такие:

а) прямоугольная изометрия (см. п. 6.2.1);

б) прямоугольная диметрия (см. п. 6.2.2);

в) косоугольная горизонтальная изометрия (см. п. 6.3.1);

г) косоугольная фронтальная изометрия (см. п. 6.3.1);

д) косоугольная фронтальная диметрия (см. п. 6.3.2).

Эти виды аксонометрического проецирования широко используются в машиностроении, строительстве и архитектуре.

Видео:ДиметрияСкачать

Прямоугольное аксонометрическое проецирование

Способ аксонометрического проецирования состоит в том, что данный предмет вместе с осями прямоугольных координат, к которым эта система относится в пространстве, параллельно проецируется на некоторую плоскость α .

Прямоугольная изометрия

Для прямоугольных аксонометрических проекций (φ = 90°) из формулы (6.1) получаем основное соотношение

Углы наклона осей к горизонту (рис. 6.1 б) определяются по таким формулам:

Прямоугольная изометрия (от греческого ισοµετρία – соизмеримость) – вид прямоугольного аксонометрического проецирования, в котором коэффициенты искажения k по осям одинаковы.

Из формулы (6.2) для случая имеем откуда ≈ 0,816. При этом по формулам (6.3) углы (рис. 6.3).

Прямоугольная изометрия

На практике с целью упрощения коэффициенты k условно считают равными единице (k = 1). Это приводит к тому, что все действительные размеры геометрических объектов увеличиваются на 23 % (1/0,816 = 1,23).

На рис. 6.4 б построена прямоугольная изометрия призмы, комплексный чертёж которой показан на рис. 6.4 а.

Прямоугольная изометрия призмы

Для построения аксонометрической проекции геометрического объекта удобно ввести локальную систему координат (от англ. local – местный) – систему координат, связанную с заданным телом. Например, на рис. 6.4 а выбрана локальная ортогональная система координат x, y, z с центром О, совпадающим с геометрическим центром основы (пятиугольника) призмы.

На рис. 6.5 а – е построены точные и приближённые прямоугольные изометрические проекции окружностей горизонтального, фронтального и профильного уровней. Например, прямоугольной изометрией окружности горизонтального уровня диаметром d является эллипс с горизонтальной осью длиной 1,22d и вертикальной осью длиной 0,71d. Этот эллипс вписан в ромб с углами при вершинах 60°, 120°.

Длины всех сторон ромба равны диаметру d заданной окружности. На практике искомый эллипс заменяется овалом (рис. 6.5 г), построенным так. Строится окружность диаметром d с центром в начале отсчёта Определяются точки пересечения этой окружности с осями аксонометрической системы координат. Определяются точки пересечения окружности с осью Строятся точки пересечения отрезков с горизонтальной линией, проходящей через центр окружности. Из точек проводятся дуги радиусом Из точек проводятся дуги радиусом . Полученный овал является приближённой изометрической проекцией окружности горизонтального уровня. Длина горизонтальной оси овала меньше соответствующей оси эллипса на 6 %. Длина вертикальной оси овала больше соответствующей оси эллипса на 4 %.

На рис. 6.5 б – в, д – е приведены точные и приближённые прямоугольные изометрические проекции окружности фронтального и профильного уровней. Отличие этих проекций от проекций окружности горизонтального уровня состоит в том, что большая ось эллипса (или овала) размещена под углом 60° к горизонту.

Прямоугольная изометрия окружности

Прямоугольная диметрия

Прямоугольная диметрия (от греческого δυο – два, µετρο – мера) – вид прямоугольного аксонометрического проецирования, в котором коэффициенты искажения по осям x, z одинаковы а по оси у вдвое меньше

Из формулы (6.2) для случая имеем откуда При этом по формулам (6.3) углы (рис. 6.6). Эти углы удобно строить так. Из точки влево откладывается отрезок длиной 8l, где l –условная длина (произвольное значение). От полученной точки вниз откладывается отрезок длиной l. Через полученную точку и начало отсчёта проходит ось х. Для построения оси у из точки вправо откладывается отрезок длиной 8l. От полученной точки вниз откладывается отрезок длиной 7l. Через полученную точку и начало отсчёта проходит ось у (рис. 6.7).

Прямоугольная димметрия

Построение осей координат

На практике с целью упрощения коэффициенты k условно считают равными единице по осям х, z и 0,5 по оси у. Это приводит к тому, что все действительные размеры геометрических объектов увеличиваются на 6 % (1/0,943 = 1,06; 0,5/0,471 = 1,06).

На рис. 6.8 б построена прямоугольная диметрия пирамиды, комплексный чертёж которой показан на рис. 6.8 а.

Прямоугольная диметрия пирамиды

На рис. 6.9 а – е построены приближённые прямоугольные изометрические проекции окружностей горизонтального, фронтального и профильного уровней. Например, прямоугольной изометрией окружности горизонтального уровня диаметром d является эллипс со взаимно перпендикулярными осями длиной соответственно 1,06d, 0,35d. Этот эллипс вписан в параллелограмм со сторонами d, 0,5d, наклонёнными под углами 7°11/ , 41°25/ к горизонту. На практике искомый эллипс заменяется овалом (рис. 6.9 г), построенным таким способом. Строится окружность диаметром d с центром в начале отсчёта Определяются точки пересечения этой окружности с осью аксонометрической системы координат. Точки отображаются симметрично горизонтальной оси. Определяются точки оси удалённые от точек на расстояние d. Строятся точки пересечения отрезков с горизонтальной линией, проходящей через центр окружности.

Из точек проводятся дуги радиусом Из точек проводятся дуги радиусом Полученный овал является приближённой диметрической проекцией окружности горизонтального уровня. Длина горизонтальной оси овала больше соответствующей оси эллипса на 4 %. Длина вертикальной оси овала больше соответствующей оси эллипса на 10 %. На рис. 6.9 б – в, д – е приведены прямоугольные диметрические проекции окружности фронтального и профильного уровней. Отличие прямоугольной диметрии окружности фронтального уровня от проекций окружностей горизонтального и профильного уровней состоит в том, что параллелограмм имеет одинаковые стороны длиной d. Большая ось овала на 1 % меньше большей оси эллипса; меньшая ось овала больше меньшей оси эллипса на 1 %.

Прямоугольная диметрия окружности

Видео:Диметрические проекции.Скачать

Косоугольное аксонометрического проецирования

Косоугольные аксонометрические проекции характеризуются двумя основными признаками: плоскость аксонометрических проекций располагается параллельно одной из граней предмета, которая изображается без искажения; направление проецирования выбирается косоугольное (составляет с плоскостью проекций острый угол), что дает возможность спроецировать и две другие грани или стороны предмета, но уже с искажением.

Косоугольная изометрия

Косоугольная изометрия – вид косоугольного аксонометрического проецирования, в котором коэффициенты искажения k по осям одинаковы. На практике используют коэффициенты k = 1.

Используются такие виды косоугольной изометрии:

а) горизонтальная изометрия, для которой углы = 60°; = 30°;

б) фронтальная изометрия, для которой углы = 0°, = 45°.

На рис. 6.10 а – б показана косоугольная горизонтальная изометрия точки и призмы, на рис. 6.11 а – в – окружностей горизонтального, фронтального и профильного уровней.

Косоугольная горизонтальная изометрия

Косоугольная горизонтальная изометрия окружности диаметром d горизонтального уровня является окружностью такого же диаметра (рис. 6.11 а). Косоугольные горизонтальные изометрии окружности диаметром d фронтального и профильного уровней являются эллипсами, вписанными в ромбы со сторонами d (рис. 6.11 б – в).

Косоугольная горизонтальная изометрия окружности

На рис. 6.12 а – б показана косоугольная фронтальная изометрия точки и призмы, на рис. 6.13 а – в – окружностей горизонтального, фронтального и профильного уровней. Косоугольная фронтальная изометрия окружности диаметром d фронтального уровня является окружностью такого же диаметра (рис. 6.13 б). Косоугольные фронтальные изометрии окружностей диаметром d горизонтального и профильного уровней являются эллипсами, вписанными в ромбы, стороны которых равны d (рис. 6.13 а, в).

Косоугольная фронтальная изометрия

Косоугольная фронтальная изометрия окружности

Косоугольная диметрия

Косоугольная диметрия – вид косоугольного аксонометрического проецирования, в котором коэффициенты искажения k по осям х, z одинаковы, а по оси у – вдвое меньший (0,5k). На практике применяют фронтальную диметрию, для которой k = 1, а углы = 0°; = 45°. На рис. 6.14 а – б показана косоугольная фронтальная диметрия точки и призмы, на рис. 6.15 а – в – окружностей горизонтального, фронтального и профильного уровней.

Косоугольная диметрия

Косоугольная фронтальная диметрия окружности диаметром d фронтального уровня является окружностью такого же диаметра (рис. 6.15 б). Косоугольные фронтальные диметрии окружности диаметром d горизонтального и профильного уровней являются эллипсами, вписанными в параллелограммы со сторонами d, d/2 (рис. 6.15 а, в).

Косоугольная диметрия окружности

Допускается построение фронтальной диметрии с углом = 30°. На рис. 6.16 а – б показана эта разновидность косоугольной фронтальной диметрии точки и призмы, на рис. 6.17 а – в – окружностей горизонтального, фронтального и профильного уровней.

Разновидность косоугольной фронтальной диметрии

Разновидность косоугольной фронтальной диметрии окружности

Видео:2 2 2 изометрия треугольника и шестиугольникаСкачать

Решение позиционных задач

Позиционные задачи – это задачи, решение, которых должно давать ответ на вопрос о взаимном расположении геометрических объектов как по отношению друг к другу, так и относительно системы координатных плоскостей проекций.

Пересечение прямой с плоскостью. пересечение двух плоскостей

Способ аксонометрического проецирования можно применить для решения задач начертательной геометрии.

Преимущества способа аксонометрического проецирования:

а) решение позиционных задач сопровождается наглядными изображениями предметов;

б) задачи решаются с помощью только одной аксонометрической проекции.

Недостатки способа аксонометрического проецирования:

а) сложность построения аксонометрических проекций геометрических объектов;

б) сложность или невозможность решения метрических задач;

в) необходимость в некоторых случаях дополнения аксонометрического изображения другой проекцией.

Для решения задач способом аксонометрического проецирования используется, как правило, прямоугольная изометрия.

На рис. 6.18*( * в дальнейшем верхний индекс не обозначается с целью упрощения обозначений) с помощью прямоугольной изометрии решена задача на нахождение пересечения прямой l с плоскостью Σ, заданной следами Через прямую l проводится горизонтально-проецирующая плоскость Ω (след параллельный оси z, след совпадает с горизонтальной проекцией l1 прямой l). По вспомогательным точкам 1, 2 строится прямая k пересечения плоскостей Σ, Ω. Точка K пересечения прямых l, k — искомая точка пересечения прямой l с плоскостью Σ.

На рис. 6.19 способом аксонометрического проецирования определяется линия пересечения плоскостей Σ, Ω, заданных следами. Определены точки 1, 2 пересечения двух пар одноимённых следов. Искомая линия k пересечения проходит через точки 1, 2.

Пересечение прямой с плоскостью Пересечение двух плоскостей

Пересечение тела плоскостью

На рис. 6.20 построена линия пересечения треугольной призмы плоскостью общего положения, заданной следами. Определяются точки 1 – 5 пересечения следов плоскости с рёбрами (точка 1) и гранями (точки 2 –5) призмы. Точки 4, 5 определены с помощью вспомогательных вертикальных линий, принадлежащих граням призмы.

Пересечение многогранника плоскостью Пересечение тела вращения плоскостью

На рис. 6.21 построена линия пересечения цилиндра плоскостью общего положения. Для её определения вводятся вспомогательные секущие плоскости фронтального уровня, пересекающие цилиндр по прямоугольникам, а плоскость – по прямым линиям. Точки 1 – 5 пересечения этих прямоугольников с соответствующими прямыми — точки искомой линии пересечения цилиндра плоскостью.

Пересечение двух тел

На рис. 6.22 построена линия пересечения цилиндра с призмой. Для её определения используются секущие плоскости профильного уровня, пересекающие цилиндр и призму по прямоугольникам. Точки 1 – 6 пересечения пар прямоугольников принадлежат искомой линии пересечения данных тел.

Пересечение тела вращения с многогранником Пересечение двух тел вращения

На рис. 6.23 построена линия пересечения конуса с цилиндром. Для её определения применяются фронтально-проецирующие секущие плоскости проходящие через вершину S конуса. Эти плоскости пересекают конус по треугольникам, а цилиндр – по прямоугольникам. Точки 1 – 8 пересечения этих треугольников с соответствующими прямоугольниками принадлежат искомой линии пересечения конуса с цилиндром.

Преобразование аксонометрических проекций

Между аксонометрическими и ортогональными проекциями существует связь, которая позволяет переходить вот одного способа проецирования к другому и определять направление проецирования. Процедура такого перехода осуществляется с помощью построения треугольника следов картинной плоскости

На рис. 6.24 а построена система осей x прямоугольной изометрии с центром в точке На оси произвольно выбирается точка , через которую проводятся отрезки первый из которых перпендикулярен оси второй – оси . Точки , принадлежат соответственно осям Полученный треугольник является треугольником следов картинной плоскости Для определения натуральной величины треугольника последний совмещается с горизонтальной плоскостью проекций П1 (см. п. 2.4.3, рис. 2.39 – 2.40). При этом точка вращается вокруг горизонтального следа до положения О. Вдоль отрезков проводятся оси х, у горизонтальной плоскости проекций П1 с центром в точке О (угол хОу прямой). Центром вращения является точка радиусом – длина отрезка

Для определения проекции А1 произвольной точки А по аксонометрической проекции в картинной плоскости строится луч и находится точка его пересечения с осью вращения Проекция А1 является точкой пересечения отрезка с линией направления вращения, перпендикулярной оси вращения

Положения плоскостей проекций П2, П3 находятся аналогично, путём вращения картинной плоскости вокруг следов соответственно (рис. 6.24 б – в).

Совмещение картинной плоскости с плоскостями проекций

Видео:Частное положение точек. Точки принадлежащие к плоскостям проекции.Скачать

Аксонометрические проекции с примерами посмотроения

Аксонометрические проекции — это способ изображения геометрических предметов на чертеже при помощи параллельных проекций.

Для изображения на плоскости какого-либо предмета используют:

а) обычный рисунок;

б) способ перспективного изображения, осно­ванный на методе центрального проецирования;

в) чертеж, состоящий из прямоугольных (орто­гональных) проекций;

г) аксонометрические проекции.

Обычный рисунок изображает предмет, как он представляется глазу наблюдателя (рис. 131). Способ перспективного изображения используют при создании архитектурных проектов (рис. 132). Применение рисунка в производстве неудобно, так как он искажает форму и размеры предмета.

Чертеж дает представление о форме и размерах предмета, но часто уступает в наглядности. В этих случаях дают дополнительно изображение этого предмета в аксонометрической проекции.

На рис. 133, а приведены ортогональные проек­ции предмета, по которым довольно трудно представить его форму. Значительно нагляднее ак­сонометрическая проекция этого предмета (рис. 133, 6).

Видео:Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Рассмотрим способ получения аксонометричес­ких проекций

На рис. 134 изображен в трех проекциях куб. Все три видимые его грани 1, 2, 3 про­ецируются без искажения. На рис. 135, а тот же куб поставлен относительно наблюдателя под углом и изображен в перспективе. Мы видим все три грани 1. 2, 3 одновременно, но все грани и ребра изображены с искаже­нием. Однако можно спроецировать куб так, чтобы видеть в проекции три грани куба с мень­шим искажением.

Для этого куб располагаем внутри трехгранного угла, образованного плоскостями проекций Н, V и W (рис. 135, б). Куб вместе с плоскостями про­екций спроецирован на аксонометрическую плос­кость проекции Р_V. Поэтому оси обозначаются со штрихами, т.е. х’, у’, z‘. Далее в обозначении штрихи убираем.

Таким образом, мы подошли к способу построе­ния аксонометрических проекций. Остается опре­делить, на какой угол целесообразнее всего повер­нуть предмет.

ГОСТ 2.317—69 устанавливает аксонометрические проекции, применяемые в чертежах всех отраслей промышленности и строительства (рис. 136).

В зависимости от направления проецирующих прямых и искажения линейных размеров предме­та аксонометрические проекции делятся на прямо­угольные и косоугольные.

Если проецирующие прямые перпендикулярны аксонометрической плоскости проекции, то такая проекция называется прямоугольной аксонометри­ческой проекцией. К прямоугольным аксономет­рическим проекциям относятся изометрическая (рис. 136. а, б) и диметрическая (рис. 136, в, г) проекции.

Если проецирующие прямые направлены не под углом 90 0 к аксонометрической плоскости проек­ций, то получается косоугольная аксонометрическая проекция. К косоугольным аксонометричес­ким проекциям относятся фронтальная изометри­ческая (рис. 136, д, е), горизонтальная изометри­ческая (рис. 136, ж, з) и фронтальная диметрическая (рис. 136, и, к) проекции.

Прямоугольные аксонометрические проекции дают наиболее наглядные изображения и поэтому чаще применяются в машиностроительном черче­нии.

Виды аксонометрических проекций, расположение аксонометрических осей и коэффициенты искажения линейных размеров показаны на рис. 136.

Видео:Построение изометрической проекциии треугольникаСкачать

Изометрическая проекция отрезков и плоских фигур

На рис. 136, а и б представлена изометрическая проекция.

Рассмотрим построение изометрической проекции куба.

Как и при ортогональном (прямоугольном) проецировании, куб расположен внутри трехгран­ного угла, образованного плоскостями проекций Н, V и W. В прямоугольной изометрической про­екции оси х, у, z расположатся под углом 120 0 друг к другу. Все три коэффициента искажения по аксонометрическим осям одинаковы и равны 0,82, поэтому длина ребер куба на изображении одинаковая и равна 0,82 действительной длины. Обычно для упрощения построений такого сокра­щения не делают; отрезки, параллельные аксоно­метрическим осям, откладывают действительной длины.

Простейшим элементом является точка, поэто­му построение изометрических проекций начнем с точки.

Если даны ортогональные проекции точек А и В (рис. 137, а), то известны их координаты. Для построения изометрической проекции этих точек проводят аксонометрические оси х, у и z под углом 120 0 друг к другу (рис. 137, б). Далее от начала координат О по оси х откладывают отре­зок, равный координате х_B точки В, в данном примере х_B = 39 мм. Получим точку 1.

Из точки 1 проводят прямую, параллельную оси у, и на ней откладывают отрезок, равный координате y_B, точку 2. Из точки 2 проводят пря­мую, параллельную оси z, на которой отклады­вают отрезок, равный координате z_B. Полученная точка В — искомая изометрическая проекция точ­ки В.

Аналогично строят изометрическую проекцию точки А. Так как координата z точки А равна нулю, то достаточно отложить координаты х и у (по соответствующим осям) точки А.

Аксонометрические оси изометрической проек­ции, а также отрезки прямых, параллельные этим осям, удобно строить с помощью угольника с уг­лами 30 и 60 0 (рис. 137, а).

Изометрическая проекция отрезка прямой АВ может быть легко построена по двум точкам — концам этого отрезка. Найдя по координатам изометрические проекции этих точек, соединим их прямой линией. По точкам может быть выпо­лнена изометрическая проекция любой фигуры. При этом расположение фигур относительно оси х, у и z может быть различным.

Рассмотрим, например, построение изометри­ческой проекции правильных пятиугольников (рис. 138). В этом случае для упрощения построе­ний рассматриваются пятиугольники, расположен­ные на плоскостях проекций Н, V, W. Тогда одна из координат вершин пятиугольника будет равна нулю и изометрическую проекцию каждой верши­ны можно строить по двум координатам, подобно построению точки А ( см. рис. 137, б).

Построив изометрические проекции вершин, соединяем их прямыми и получаем изометричес­кую проекцию прямоугольника.

Видео:Треугольная призма. Ортогональные и изометрическая проекции. Урок 10.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Изометрическая проекция окружности

На рис. 139 изображена изометрическая проек­ция куба с окружностями, вписанными в его гра­ни. Квадратные грани куба будут изображаться в виде ромбов, а окружности в виде эллипсов. Надо запомнить, что малая ось CD каждого эллипса всегда должна быть перпендикулярна большой оси АВ.

Если окружность расположена в плоскости, параллельной плоскости Н, то большая ось АВ должна быть перпендикулярна оси z, а малая ось CD— параллельна оси z (рис. 139).

Если окружность расположена в плоскости, параллельной плоскости V, то большая ось эллип­са должна быть проведена под углом 90 0 к оси у.

При расположении окружности в плоскости, параллельной плоскости W, большая ось эллипса располагается под углом 90 0 к оси х.

Заметим, что большие оси всех трех эллипсов направлены по большим диагоналям ромбов.

При построении изометрической проекции ок­ружности без сокращения по осям х, у и z длина большой оси эллипсов берется равной 1,22 диа­метра d изображаемой окружности, а длина малой оси эллипса — 0,71 d (рис. 139).

В учебных чертежах вместо эллипсов рекомен­дуется применять овалы, очерченные дугами ок­ружностей. Упрощенный способ построения ова­лов приведен на рис. 140.

Для построения овала соответствующей изометрической проекции окружности, параллельной плоскости Н, проводят вертикальную и горизон­тальную оси овала (рис. 140, а). Из точки пересе­чения осей О проводят вспомогательную окруж­ность диаметром d, равным действительной вели­чине диаметра изображаемой окружности, и нахо­дят точки n₁, n₂. n₃, n₄ пересечения этой окруж­ности с аксонометрическими осями х и у. Из то­чек m₁ и m₂ пересечения вспомогательной окруж­ности с осью z, как из центров радиусом R = m_1* n₃, проводят две дуги 23 и 14, принадлежащие овалу. Пересечения этих дуг с осью z дают точки С и D.

Из центра О радиусом ОС, равным половине малой оси овала, засекают на большой оси овала АВ точки О₁ и О₂. Точки 1, 2, 3 и 4 сопряжений дуг радиусов R и R₁ находят, соединяя точки m_t и т₂ с точками O₁ и О₂ и продолжая прямые до пересечения с дугами 23 и 14. Из точек O₁ и О₂ радиусом R₁=0,1 проводят две дуги.

Так же строят овалы. расположенные в плос­костях, параллельных плоскостям V и W (рис. 140, б и в).

Видео:Шестиугольник в изометрииСкачать

Изометрическая проекции геометрических тел

Изображение геометрического тела в изометри­ческой проекции, например правильной шести­угольной призмы, выполняют и такой последова­тельности (рис. 141).

Если основные призмы — правильный много­угольник (например, шестиугольник), то построе­ние вершин основания по координатам можно упростить, проведя одну из осей координат через центр основания. На рис. 141 оси х, у и z проведе­ны через центры правильных шестиугольников призмы.

Построив изометрическую проекцию основания призмы, из вершин шестиугольника основания проводим прямые, параллельные соответственно осям х, у или z (для каждой из рассматриваемых на рис. 141 призм). На этих прямых от вершин основания отложим высоту призмы и получим точки 1, 2, 3, 4, 5, 6 вершин другого основания призмы. Соединив эти точки прямыми, получим изометрическую проекцию призмы. В заключение устанавливаем видимые и невидимые линии; не­видимые линии надо проводить штриховыми ли­ниями.

На рис. 142 показано построение изометричес­кой проекции плоской детали криволинейного очертания по комплексному чертежу. Деталь (рис. 142, а и б) расположена параллельно фронтальной плоскости проекций. На фронтальной проекции комплексного чертежа намечают ряд точек и строят их на изометрической проекции (рис. 142, в).

Через построенные точки контура кулачка про­водят по лекалу кривую линию.

Параллельно оси у от найденных точек проводят прямые линии, на которых отклады­вают отрезки, равные А (толщине детали). Соединяя новые точки, получают контур дру­гой плоскости детали, который также обводят по лекалу.

Аналогично строят по чертежу изометрическую проекцию кулачка.

На рис. 143 показано построение изометричес­кой проекции (рис. 143, в) неправильной пятиу­гольной пирамиды по ее комплексному чертежу (рис. 143, а). Определяем координаты всех точек основания пирамиды, затем по координатам x и y строим изометрическую проекцию пяти точек — вершин основания пирамиды А, В, С. D, Е. Например, изометрическая проекция точки А получается следующим образом.

По оси х от намеченной точки О откладываем координату х_А — a‘d. Из конца ее провопим пря­мую, параллельную оси у, на которой откладыва­ем вторую координату этой точки у_А = a‘d.

Далее строят по координатам высоту пирамиды и получают точку S — вершину пирамиды. Соеди­няя точку S с точками А. В. С, D н Е, получают изометрическую проекцию пирамиды.

Последовательность построения изометрической проекции детали по данному комплексному черте­жу (рис. 144, а) показана на рис. 144, (6 — г). Деталь мысленно разделяют на отдельные простей­шие геометрические элементы, в данном случае на призматические элементы (рис. 144, б). Нахо­дят центры окружностей (рис. 144, в). Затем уда­ляют лишние построения, контур изображения обводят сплошной основной линией (рис. 144, г).

Для выявления внутренней формы предмета применяют вырез одной четверти детали. Вырез в аксонометрических проекциях можно строить двумя способами.

Первый способ. Вначале строят в тонких линиях аксонометрическую проекцию (рис. 145, а). Затем выполняют вырез, направляя две секущие плоскости по осям х и у (рис. 145, б). Удаляют часть изображаемого предмета (рис. 145, в), после чего штрихуют сечения и обводят изображение сплошными толстыми лини­ями (рис. 145, г).

Второй способ построения разреза при изображении деталей и аксонометрической проекции показан на рис. 146, а. Сначала строят аксонометрические проекции фигур сечения, а затем дочерчивают части изобра­жения предмета, расположенные за секущими плоскостями (рис. 146. б).

Второй способ упрощает построение, освобожда­ет чертеж от лишних линий.

Линии штриховки сечений в аксонометрических проекциях наносят, как показано на рис. 147, а, параллельно диагоналям проекции квадратов, которые лежат в плоскостях проекций и стороны которых параллельны аксонометрическим осям.

Штриховку сечений к изометрической проекции удобно выполнять угольником с углами 30 и 60 0 (рис. 147, б).

Изометрическая проекция шара (рис. 148) вы­полняется следующим образом. Из намеченного центра О проводят окружность диаметра, равною 1,22d (d — диаметр шара); это и будет изображе­ние шара в изометрической проекции.

Если требуется построить половину, четверть или три четверти шара, то необходимо сначала вычертить овалы (рис. 148), большие оси которых АВ и CD перпендикулярны осям z и у. Тогда овалы и точки т и п пересечения этих овалов опре­делят границы трех четвертей шара.

Видео:ПОСТРОИТЬ ИЗОМЕТРИЧЕСКУЮ И ДИМЕТРИЧЕСКУЮ ПРОЕКЦИЮ ПО ДВУМ ВИДАМ [isometry and dimetric projection]Скачать

Диметрическая проекция

В диметрической проекции ось z — вертикаль­ная; ось х расположена под утлом 7 0 10′, а ось у — под утлом 41 0 25′ к горизонтальной прямой (см. рис. 136, в и г).

Коэффициенты искажения по осям х и z равны 0.94. а по оси у — 0,47, но обычно отрезки пря­мых по осям х и у откладывают без искажения, а по оси у коэффициент искажения берут 0,5.

Все отрезки прямых линий предмета, которые были параллельны осям х, у и z на комплексном чертеже, останутся параллельными соответствую­щим осям в диметрической проекции.

Положение плоскости фигуры относительно осей диметрической проекции может быть различ­ным. На рис. 149 показано, как изменяется изо­бражение фигуры и диметрии

в зависимости от того, на какой из плоскостей проекций расположена фигура. Это изменение вызывается тем об­стоятельством, что при построении вершин много­угольника их координаты по оси у в диметрической проекции сокращаются вдвое против действительной величины. Например, высота h фигуры, расположенной в плоскости H. и длина l фигуры, расположенной в плоскости W, уменьшаются в два раза.

В диметрической проекции изображения гео­метрических тел строят так же, как в изометри­ческой. с учетом коэффициента искажения по оси у.

На рис. 150 показано изображение треугольной призмы в диметрической проекции. Если ребра призмы параллельны оси х или z, то размер их высоты нс меняется, но искажается форма основа­ния. При расположении ребер параллельно оси у сокращается вдвое их высота.

Видео:Шестиугольная призма.Ортогональные и изометрическая проекции.Урок 17.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Диметрическая проекция окружности

Окружности в диметрической проекции изобра­жаются в виде эллипсов. Большая ось АВ эллип­сов во всех случаях равна 1,06 d, где d — диаметр окружности. Малые оси CD эллипсов, располо­женных на плоскостях, параллельных плоскости проекций W и H, равны 0,35 d, а на плоскости, параллельной плоскости V, — O.95 d (рис. 151 ).

В диметрической проекции окружности эллип­сы иногда заменяются овалами. На рис. 152 при­ведены примеры построения диметричеcких про­екций окружностей, где эллипсы заменены овала­ми, построенными упрошенным способом.

Разберем упрощенное построение диметрической проекции окружности, расположенной параллельно фронтальной плоскости проекций (рис. 152, а).

Через точку О проводим оси, параллельные осям х и z. Из центра О радиусом, равным радиу­су данной окружности, проводим вспомогательную окружность, которая пересекается с осями х и z в точках 1, 2, 3, 4.

Из точек 1 и 3 (по направлению стрелок) про­водим горизонтальные линии до пересечения с осями АВ и CD овала и получаем точки О₁ О₂, О₃ и О₄. Приняв за центры точки О₁ и О₄ радиу­сом R = О₄1, проводим дуги 12 и 34. Приняв за центры точки О₂ и О₃, проводим радиусом R₁= 0₂2 замыкающие овал дуги 23 и 14. Большая ось АВ овала примерно будет равняться 1.06d, а малая CD— 0,95d.

Построение диметрической проекции окружнос­ти, лежащей в плоскости, параллельной профиль­ной плоскости проекции W, приведено на рис. 152, б.

Из центра О проводим прямые, параллельные осям х и z, а также большую ось овала AB пер­пендикулярно малой оси CD. CD параллельна оси х. Из точки О радиусом, равным радиусу данной окружности, проводим вспомогательную окруж­ность и получаем точки п и п₁.

На прямой, параллельной оси х, вправо и влево от центра О откладываем отрезки, равные диамет­ру вспомогательной окружности, и получаем точ­ки О₁ и О₂. Приняв эти точки за центры, прово­дим (по направлению стрелок) радиусом R = O_tn = О₂n₁ дуги овалов. Пересечения получен­ных дуг с вспомогательной окружностью дают точки n₂ и n_3. Соединяя точки О₂ и n_1, О₂ и n₂ прямыми на линии большой оси АВ овала, полу­чим точки О₃ и О₄. Приняв их за центры, проводим радиусом R, замыкающие овал дуги.

На рис. 152, в показано аналогичное упрошен­ное построение диметрнческой проекции окруж­ности, расположенной в плоскости, параллельной горизонтальной плоскости проекций.

Видео:Как начертить конус в объемеСкачать

Выполнение диметрических проекций деталей

Последовательность выполнения детали в диметрической проекции показана на рис. 153.

Деталь мысленно разделяют на отдельные про­стейшие геометрические элементы, в данном при­мере — на прямоугольные параллелепипеды (рис. 153, а). По оси у откладывают половину соответствующей длины ребра.

Далее находят положения центров отверстий в детали, используя метод координат, и строят ова­лы. Разрез детали выполняют по двум плос­костям. параллельным плоскостям V и W. На таком разрезе видно, что отверстия с верти­кальными и горизонтальными осями — цилиндрические сквозные. Затем удаляют линии по­строения, контур изображения обводят сплош­ной основной линией (рис. 153, б) и штрихуют сечения (рис. 153, в).

Видео:Как построить точки в системе координат OXYZСкачать

Фронтальная изометрическая проекция

Положение аксонометрических осей при изо­бражении предметов в фронтальной изометричес­кой проекции показано на рис. 136, д и е.

Фронтальную изометрическую проекцию выполняют без искажения по осям х, у и z. Все изобра­жения, лежащие в плоскостях, параллельных фронтальной плоскости проекций, изображаются без искажения (рис. 136, д, е и рис. 154, а).

Окружности, расположенные в плоскостях, параллельных фронтальной плоскости проекций, проецируются на аксонометрическую плоскость проекции в окружности без искажения по осям.

Окружности, лежащие в плоскостях, парал­лельных плоскостям проекций Н и W, проециру­ются в эллипсы.

Для построения эллипсов из центров О радиу­сом, равным радиусу данной окружности, прово­дим вспомогательные окружности. Через центры О проводят прямые под утлом 22 0 30′ к аксономет­рическим осям х и z и от центра откладывают большие оси эллипсов. Малые оси эллипсов до­лжны быть перпендикулярны большим.

Длина большой оси эллипса равна 1,3d, а ма­лой — 0.54d, где d

Предмет во фронтальной изометрической про­екции следует располагать относительно осей так, чтобы окружности дуги плоских кривых находи­лись в плоскостях, параллельных фронтальной плоскости проекций (рис. 154, б). Тогда построе­ние их упрощается, так как они изображаются без искажений.

Видео:ВМ Диметрия перенос точекСкачать

Горизонтальная изометрическая проекция

Положения аксонометрических осей горизон­тальной изометрической проекции показаны на рис. 136, ж и з.

В горизонтальной изометрической проекции линейные размеры предметов изображаются без искажения по всем трем осям. При построении осей пользуются угольниками с углами 30 и 60 0 , как показано на рис. 155, а.

Окружность, расположенная в плоскости, па­раллельной плоскости Н, проецируется в окруж­ность того же диаметра (рис. 155, б, окружность 2). Окружности, лежащие в плоскостях, парал­лельных плоскостям проекций V и W,— в эллип­сы (рис. 155, б, эллипсы 1 и 3).

Большая ось эллипса 1 равна 1.37d, а малая — 0,37d (d — диаметр изображаемой окружности). Большая ось эллипса 3 равна 1,22d, а малая — 0,71d.

На рис. 155, в изображена деталь в горизон­тальной изометрической проекции.

Видео:построение фронтальной и изометрической проекцииСкачать

Косоугольная фронтальная диметрическая проекция

Положения аксонометрических осей фронталь­ной диметрической проекции показаны на рис. 136, и и к. Допускается применять фронталь­ные диметрические проекции с углом наклона оси у 30 и 60 0 . Длина отрезков прямых, отложенных в направлении осей х и z, выполняется без иска­жения, а в направлении оси у линейные размеры сокращают вдвое (см. рис. 136, и и к). Эго можно видеть и на рис. 156, а—в, где даны фронтальные проекции призм и пирамиды. На рис. 156, а осно­вание призмы (правильный шестиугольник) иска­жено, а на рис. 156, в — без искажения.

Окружность, лежащая в плоскости, параллель­ной фронтальной плоскости проекций (см. рис. 136, и и к), проецируется на аксонометричес­кую плоскость проекций в окружность того же диаметра, а окружности, лежащие в плоскостях, параллельных профильной и горизонтальной плос­костям проекций, — в эллипсы. Большая ось эл­липсов равна l,07d, а малая ось — 0,33d (d — диаметр окружности). Для упрощения построения эллипсы заменяют овалами.

Линии штриховки сечений в аксонометрических проекциях наносят параллельно одной из диагона­лей проекций квадратов, лежащих в соответствующих координатных плоскостях, стороны кото­рых параллельны аксонометрическим осям (рис. 157, а). При нанесении размеров выносные линии проводят параллельно аксонометрическим осям, размерные линии — параллельно измеряе­мому отрезку (рис. 157, б).

В аксонометрических проекциях спицы махови­ков и шкивов, ребра жесткости и подобные эле­менты штрихуют (рис. 158. а).

При выполнении в аксонометрических проекци­ях зубчатых колес, реек, червяков, резьб и подо­бных элементов допускается применять условнос­ти по ГОСТ 2.402-68 и ГОСТ 2.311-68 (рис. 158, б и в).

Примеры и образцы решения задач:

Услуги по выполнению чертежей:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Построение равнобедренного треугольникаСкачать

Как построить диметрию треугольника

Раздел 2: Проецирование (6 часов)

Урок № 9: Рациональные построения в изометрии. Проекции плоских фигур и окружности

Ботвинников А.Д. § 7.2-7.3, 8 [1]

Степакова В. В. § 23 [3]
Вышнепольский И.С. § 13-14 [8]

В ряде случаев построение аксонометрических проекций удобнее начинать с построения фигуры основания. Поэтому рассмотрим, как изображают в аксонометрии плоские геометрические фигуры, расположенные горизонтально.

1. Построение аксонометрической проекции квадрата показано на рис. 1, а и б.

Вдоль оси х откладывают сторону квадрата а, вдоль оси у — половину стороны а/2 для фронтальной диметрической проекции и сторону а для изометрической проекции. Концы отрезков соединяют прямыми.

Рис. 1. Аксонометрические проекции квадрата:

а — фронтальная диметрическая; б — изометрическая

2. Построение аксонометрической проекции треугольника показано на рис. 2, а и б.

Симметрично точке О (началу осей координат) по оси х откладывают половину стороны треугольника а/2, а по оси у — его высоту h (для фронтальной диметрической проекции половину высоты h/2). Полученные точки соединяют отрезками прямых.

Рис. 2. Аксонометрические проекции треугольника:

а — фронтальная диметрическая; б — изометрическая

3. Построение аксонометрической проекции правильного шестиугольника показано на рис. 3.

По оси х вправо и влево от точки О откладывают отрезки, равные стороне шестиугольника. По оси у симметрично точке О откладывают отрезки s/2, равные половине расстояния между противоположными сторонами шестиугольника (для фронтальной диметрической проекции эти отрезки уменьшают вдвое). От точек m и n, полученных на оси у, проводят вправо и влево параллельно оси х отрезки, равные половине стороны шестиугольника. Полученные точки соединяют отрезками прямых.

Рис. 3. Аксонометрические проекции правильного шестиугольника:

а — фронтальная диметрическая; б — изометрическая

4. Построение аксонометрической проекции окружности .

Фронтальная диметрическая проекция удобна для изображения предметов с криволинейными очертаниями, подобных представленными на рис. 4.

Рис.4. Фронтальные диметрические проекции деталей

На рис. 5. дана фронтальная диметрическая проекция куба с вписанными в его грани окружностями. Окружности, расположенные на плоскостях, перпендикулярных к осям х и z, изображаются эллипсами. Передняя грань куба, перпендикулярная к оси у, проецируется без искажения, и окружность, расположенная на ней, изображается без искажения, т. е. описывается циркулем.

Рис.5. Фронтальные диметрические проекции окружностей, вписанных в грани куба

Построение фронтальной диметрической проекции плоской детали с цилиндрическим отверстием .

Фронтальную диметрическую проекцию плоской детали с цилиндрическим отверстием выполняют следующим образом.

1. Строят очертания передней грани детали, пользуясь циркулем (рис. 6, а).

2. Через центры окружности и дуг параллельно оси у проводят прямые, на которых откладывают половину толщины детали. Получают центры окружности и дуг, расположенных на задней поверхности детали (рис. 6, б). Из этих центров проводят окружность и дуги, радиусы которых должны быть равны радиусам окружности и дуг передней грани.

3. Проводят касательные к дугам. Удаляют лишние линии и обводят видимый контур (рис. 6, в).

Рис. 6. Построение фронтальной диметрической проекции детали с цилиндрическими элементами

Изометрические проекции окружностей .

Квадрат в изометрической проекции проецируется в ромб. Окружности, вписанные в квадраты, например, расположенные на гранях куба (рис. 7), в изометрической проекции изображаются эллипсами. На практике эллипсы заменяют овалами, которые вычерчивают четырьмя дугами окружностей.

Рис. 7. Изометрические проекции окружностей, вписанных в грани куба

Построение овала, вписанного в ромб.

1. Строят ромб со стороной, равной диаметру изображаемой окружности (рис. 8, а). Для этого через точку О проводят изометрические оси х и у, и на них от точки О откладывают отрезки, равные радиусу изображаемой окружности. Через точки a, b , с и d проводят прямые, параллельные осям; получают ромб. Большая ось овала располагается на большой диагонали ромба.

2. Вписывают в ромб овал. Для этого из вершин тупых углов (точек А и В) описывают дуги радиусом R, равным расстоянию от вершины тупого угла (точек А и В) до точек a, b или с, d соответственно. От точки В к точкам а и b проводят прямые (рис. 8, б); пересечение этих прямых с большей диагональю ромба дает точки С и D, которые будут центрами малых дуг; радиус R₁ малых дуг равен Са ( Db). Дугами этого радиуса сопрягают большие дуги овала.

Рис. 8. Построение овала в плоскости, перпендикулярной оси z.

Так строят овал, лежащий в плоскости, перпендикулярной к оси z (овал 1 на рис. 7). Овалы, находящиеся в плоскостях, перпендикулярных к осям х (овал 3) и у (овал 2), строят так же, как овал 1., только построение овала 3 ведут на осях у и z (рис. 9, а), а овала 2 (см. рис. 7) — на осях х и z (рис. 9, б).

Рис. 9. Построение овала в плоскостях, перпендикулярных осям х и у

Построение изометрической проекции детали с цилиндрическим отверстием .

Если на изометрической проекции детали нужно изобразить сквозное цилиндрическое отверстие, просверленное перпендикулярно передней грани, представленное на рисунке. 10, а.

Построения выполняет следующим образом.

1. Находят положение центра отверстия на передней грани детали. Через найденный центр проводят изометрические оси. (Для определения их направления удобно воспользоваться изображением куба на рис. 7.) На осях от центра откладывают отрезки, равные радиусу изображаемой окружности (рис. 10, а).

2. Строят ромб, сторона которого равна диаметру изображаемой окружности; проводят большую диагональ ромба (рис. 10, б).

3. Описывают большие дуги овала; находят центры для малых дуг (рис. 10, в).

4. Проводят малые дуги (рис. 10, г).

5. Строят такой же овал на задней грани детали и проводят касательные к обоим овалам (рис. 10, д).

Рис. 10. Построение изометрической проекции детали с цилиндрическим отверстием

Практические задания, тесты и домашние работы

Вопросы для повторения

pdf Вопросы

pdf

Предыдущий урок	Поурочное планирование	Следующий урок