Осевая симметрия треугольника авс (7 видео)

Осевая симметрия

Осевая симметрия — это симметрия относительно прямой.

Пусть дана некоторая прямая g.

Чтобы построить точку, симметричную некоторой точке A относительно прямой g, надо:

1) Провести из точки A к прямой g перпендикуляр AO.

2) На продолжении перпендикуляра с другой стороны от прямой g отложить отрезок OA1, равный отрезку AO: OA1=AO.

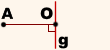
Полученная точка A1 симметрична точке A относительно прямой g.

Прямая g называется осью симметрии.

Таким образом, точки A и A1 симметричны относительно прямой g, если эта прямая проходит через середину отрезка AA1 и перпендикулярна к нему.

Если точка A лежит на прямой g, то симметричная ей точка есть сама точка A.

Преобразование фигуры F в фигуру F1, при котором каждая её точка A переходит в точку A1, симметричную относительно данной прямой g, называется преобразованием симметрии относительно прямой g.

Фигуры F и F1 называются фигурами, симметричными относительно прямой g.

Чтобы построить треугольник, симметричный данному относительно прямой g, достаточно построить точки, симметричные вершинам треугольника, и соединить их отрезками.

Например, треугольники ABC и A1B1C1 симметричны относительно прямой g.

Если преобразование симметрии относительно прямой g переводит фигуру в себя, то такая фигура называется симметричной относительно прямой g, а прямая g называется её осью симметрии.

Симметричная фигура своей осью симметрии делится на две равные половины. Если симметричную фигуру нарисовать на бумаге, вырезать и согнуть по оси симметрии, то эти половинки совпадут.

Примеры фигур, симметричных относительно прямой.

1) Прямоугольник.

Прямоугольник имеет 2 оси симметрии: прямые, проходящие через точку пересечения диагоналей параллельно сторонам.

Ромб имеет две оси симметрии:

прямые, на которых лежат его диагонали.

3) Квадрат, как ромб и прямоугольник, имеет четыре оси симметрии: прямые, содержащие его диагонали, и прямые, проходящие через точку пересечения диагоналей параллельно сторонам.

Окружность имеет бесконечное множество осей симметрии:

любая прямая, содержащая диаметр, является осью симметрии окружности.

Прямая также имеет бесконечное множество осей симметрии: любая перпендикулярная ей прямая является для данной прямой осью симметрии.

Равнобедренная трапеция — фигура, симметричная относительно прямой,перпендикулярной основаниям и проходящей через их середины.

Равнобедренный треугольник имеет одну ось симметрии:

прямую, проходящую через высоту (медиану, биссектрису), проведённую к основанию.

8) Равносторонний треугольник.

Равносторонний треугольник имеет три оси симметрии:

прямые, содержащие его высоты (медианы, биссектрисы).

Угол — фигура, симметричная относительно прямой, содержащей его биссектрису.

Осевая симметрия является движением.

Содержание

Осевая и центральная симметрия
Что такое симметрия
Осевая симметрия
Центральная симметрия
Задачи на самопроверку
«Осевая симметрия» ( 9 класс)
Главная > Документ
📺 Видео

Видео:Осевая симметрия. 6 класс.Скачать

Осевая и центральная симметрия

О чем эта статья:

Видео:Осевая и центральная симметрия, 6 классСкачать

Что такое симметрия

Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.

Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.

Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.

Рассмотрите фигуры с осевой и центральной симметрией.

Ось симметрии угла — биссектриса.
Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
Оси симметрии прямоугольника проходят через середины его сторон.
У ромба две оси симметрии — прямые, содержащие его диагонали.
У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
Ось симметрии окружности — любая прямая, проведенная через ее центр.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.

Видео:Осевая симметрия, как начертить треугольники симметричноСкачать

Осевая симметрия

Вот как звучит определение осевой симметрии:

Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.

Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

Пример 1. Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC относительно прямой.

Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
С другой стороны прямой отложим такие же расстояния.
Соединяем точки отрезками и строим треугольник A₁B₁C₁, симметричный треугольнику ABC.
Получаем два треугольника, симметричных относительно оси симметрии.

Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
Измеряем расстояние от вершин до точек на прямой.
Откладываем такие же расстояния на другой стороне оси симметрии.
Соединяем точки и строим треугольник A₁B₁C₁.

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно прямой l.

Проводим через точку А прямую, перпендикулярную прямой l.
Проводим через точку В прямую, перпендикулярную прямой l.
Измеряем расстояния от точек А и В до прямой l.
Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A₁ и B₁.
Соединяем точки A₁ и B₁.

Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!

Видео:Центральная симметрияСкачать

Центральная симметрия

Теперь поговорим о центральной симметрии — вот ее определение:

Центральной симметрией называется симметрия относительно точки.

Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.

Пример 1: Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC, относительно центра (точки О).

Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
Получившиеся точки соединяем отрезками A₁B₁ A₁C₁ B₁C₁.
Получаем треугольник A₁B₁C₁, симметричный треугольнику ABC, относительно центра.

Пример 2. Построить отрезок A₁B₁, симметричный отрезку AB относительно центра (точки О).

Измеряем расстояние от точки B до точки О и от точки А до точки О.
Проводим прямую из точки А через точку О и выводим ее на другую сторону.
Проводим прямую из точки B через точку О и выводим ее на другую сторону.
Чертим на противоположной стороне отрезки А₁О и B₁О, равные отрезкам АО и АB.
Соединяем точки A₁ и B₁ и получаем отрезок A₁B₁, симметричный данному.

Видео:ВПР 6 класс. 12 задание. Фигура симметиичная данной относительно оси.Скачать

Задачи на самопроверку

В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!

Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.

Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:

Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная

Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М₁ и N₁ — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М₁N₁.

Подсказка: опустите перпендикуляры из точек N и N₁ на прямую MМ₁.

Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.

Видео:8 класс, 9 урок, Осевая и центральная симметрияСкачать

«Осевая симметрия» ( 9 класс)

Главная > Документ

Информация о документе
Дата добавления:
Размер:
Доступные форматы для скачивания:

Тема: «Осевая симметрия» ( 9 класс)

Тип занятия: Занятие комплексного применения знаний, умений и навыков

— усвоение умений самостоятельно и с помощью учителя в комплексе применять знания, умения и навыки;

— усвоение умений осуществлять перенос знаний и умений в новые условия;

— воспитание у учащихся способности творчески мыслить, предлагать свои решения, защищать свою точку зрения;

— воспитание корректного отношения друг к другу при ведении дискуссии,

— воспитание аккуратности при работе в тетради, у доски.

Форма проведения: объяснение учителя, активное взаимодействие учителя с учащимися.

— листы с условиями задач;

— карточка с анализом задачи №4;

— карточки с рефлексией.

— листы цветной бумаги, ножницы

«Симметрия… есть идеал, с помощью которой человек веками пытался объяснить и создать порядок, красоту и совершенство»

1. Мотивация учащихся.

Тема нашего сегодняшнего занятия «Осевая симметрия».

— проникнуться красотой, гармоничностью симметричных фигур;

— вспомнить свойства симметрии;

— решить ряд задач, используя метод осевой симметрии;

В древности слово «симметрия» употреблялось в значении «гармония», «красота». Действительно, в переводе с греческого это слово означает «соразмерность, пропорциональность, одинаковость в расположении частей»

Посмотрите на кленовый лист, снежинку, бабочку. Их объединяет то, что они симметричны, каждая имеет ось симметрии. Если симметричную фигуру сложить пополам вдоль оси симметрии, то её части совпадут.

Издавна человек использовал симметрию в архитектуре. Древним храмам, башням средневековых замков, современным зданиям она придает гармоничность, законченность.

Заглянем в нашу мастерскую. Осевая симметрия поможет нам в создании симметричных фигур, например снежинок. Что бы вырезать снежинку лист бумаги, чаще квадратный складывается пополам, с помощью транспортира отмечается угол в 60 0 . Складывается бумага вдоль одной из сторон угла, затем вдоль другой из сторон угла, потом еще раз перегибается угол вдоль его биссектрисы. В сложенной бумаге вырезается ножницами узор так, что бы одновременно были прорезаны все слои бумаги. Форма узора может быть любой.

Все линии сгиба снежинки являются её осями симметрии. Это довольно хорошо видно на данной заготовке

Посчитайте, сколько осей симметрии имеют ваши снежинки.

У настоящих природных снежинок шесть осей симметрии, так что ваши снежинки почти как настоящие. Давайте несколько секунд полюбуемся на красоту, созданную самой природой

2. Повторение ранее изученного материала

Как вы уже знаете, слово симметрия в переводе с греческого означает «одинаковость в расположении частей» В таком широком понимании симметрия не имеет математического содержания. Математики вкладывают в это понятие точный математический смысл, рассматривают некоторые специальные виды симметрии. В результате симметрия становится мощным средством математических исследований, помогает решать трудные задачи. А для того чтобы освоить «метод симметрии» надо вспомнить основные свойства симметрии.

— Для любой точки плоскости всегда можно построить симметричную ей точку относительно некоторой прямой (рис.1)

— Отрезок, соединяющий симметричные точки, перпендикулярен оси симметрии и делится ею пополам (рис.2)

— Если отрезок МN симметричен отрезку M 1 N 1 относительно прямой l, то их длины равны (рис. 3)

— Если точка А 1 симметрична точке А относительно прямой l, то для любой точки В на этой прямой отрезки A 1 B и АВ равны (рис.4)

-Биссектриса угла является его осью симметрии (рис.5)

Все задачи сегодняшнего урока связаны с построением. Мы с вами уже умеем выполнять построения биссектрисы угла, серединного перпендикуляра, опускать перпендикуляр из точки на прямую. Эти действия нами были отработаны ранее, поэтому сегодня мы только вспомним как выполняются эти построения и в дальнейшем этот момент будем опускать, изображая на чертеже уже готовый результат.

Построение биссектрисы угла.

Построение серединного перпендикуляра.

Построение перпендикуляра, проведенного из точки к прямой.

3.Решение задач по теме

Задача 1. С помощью осевой симметрии постройте разность сторон ВС и ВА треугольника АВС.

Построим точку А 1 симметричную точке А относительно угла В.

Так как биссектриса угла В является осью симметрии угла В, то точка А 1 симметричная точке А будет принадлежать ВС. Отрезок А 1 С будет являться разностью сторон ВС и ВА. Действительно, А 1 С = ВС — ВА 1 = ВС — ВА, так как ВА 1 = ВА по свойству симметрии.

Сейчас немного отдохнем. Звучит приятная музыка, на экране сменяют друг друга картины природы. Сделайте несколько движений головой, плечами, прикройте глаза, расслабьтесь. Продолжаем работать.

Задача 2. Дана прямая и две точки А и В, расположенные по одну сторону от неё. Найдите на прямой такую точку С, чтобы треугольник АВС имел наименьший периметр.

Решение

Построим точку С следующим образом: построим точку В 1 симметричную точке В относительно прямой l. Соединим точки В 1 и А. Отрезок В 1 А пересекает прямую l в точке С. Треугольник АВС имеет наименьший периметр. Докажем это. Возьмем на прямой l любую другую точку С 1 и покажем, что Р АВС 1 > Р АВС . Р АВС 1 = АС 1 + ВС 1 + АВ = АС 1 + В 1 С 1 + АВ > АВ 1 +АВ =АС + В 1 С + АВ = АС + ВС + АВ = Р АВС. Точка С – искомая.

Задача 3. Дан угол с вершиной в точке А и точка М, принадлежащая одной из его сторон. Найдите на другой стороне этого угла такую точку Р, что сумма расстояний от точки Р до точек М и А равна длине данного отрезка.

Решение

На стороне угла А, не содержащей точку М отложим отрезок АК равный заданному отрезку СD. Для отрезка МК построим серединный перпендикуляр l. Точка М симметрична К относительно прямой l. Точку пересечения прямой l со стороной угла обозначим буквой Р. Докажем, что нами построена искомая точка. АР + РМ = АР + РК = АК = СD. (МР = РК по свойству симметрии).

Задача 4. Дана одна из вершин треугольника и две прямые, которым принадлежат биссектрисы этого треугольника, не содержащие данной вершины. Постройте этот треугольник.

Мы знаем, что биссектрисы углов являются их осями симметрии. По свойству симметрии точка А 1 симметричная точке А относительно биссектрисы l 1 принадлежит прямой ВС. Точка А 2 симметричная точке А относительно биссектрисы l 2 принадлежит прямой ВС. Следовательно А 1 и А 2 определяют прямую ВС. В – точка пересечения биссектрисы l 1 и прямой ВС. С – точка пересечения биссектрисы l 2 и прямой ВС.

Следуя проведенному анализу, мы можем построить еще две вершины нашего треугольника. Строим точку А 1 симметричную точке А относительно биссектрисы l 1 , точку А 2 симметричную точке А относительно биссектрисы l 2 , проводим через эти точки прямую, отмечаем точки пересечения прямой А 1 А 2 с биссектрисами и получаем еще две вершины треугольника. Треугольник АВС – искомый.

4.Подведение итогов и рефлексия

Наше сегодняшнее занятие первое в серии занятий посвященных идее геометрических преобразований. Осевая симметрия – мощный инструмент, с помощью которого решается ряд непростых задач, и вы сегодня в этом убедились. Тема непростая, требует внимания, сосредоточенности, умственного напряжения, однако, на мой взгляд, очень полезная.

А сейчас выполните последние задание нашего занятия – ответьте на вопрос: Как вы себя чувствовали во время занятия? Оцените его по трем аспектам: сложность, увлекательность, полезность.

— Занятие интересное, полезное, особых сложностей я не испытывал;

— Занятие интересное, несомненно, полезное, но довольно сложные задачи;

— На мой взгляд, тема занятия полезная, но непростая, иногда испытывал затруднения при решении задач,

— Тема занятия показалась мне сложной, испытывал трудности при решении задач, чувствую усталость;