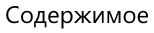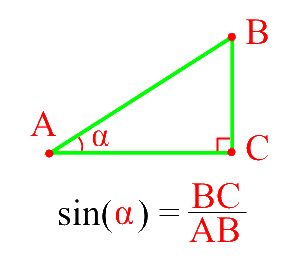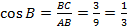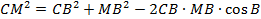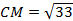- Синус, косинус и тангенс острого угла прямоугольного треугольника
- Калькулятор и таблица для вычисления синуса и косинуса.
- Калькулятор для вычисления синуса и косинуса
- Синус острого угла прямоугольного треугольника.
- Косинус острого угла прямоугольного треугольника.
- Теорема косинусов и синусов
- Формулировка и доказательство теоремы косинусов
- Формулировка теоремы для каждой из сторон треугольника
- Косинусы углов треугольника
- Определение угла с помощью косинуса
- Рассмотрение пределов изменения cos α и sin α
- Примеры решения задач
- Найдите косинус меньшего угла треугольника, стороны которого 2 см 3 см 4смА)3 / 7 Б)3 / 8 В)5 / 8 Г)7 / 8 Д)5 / 7С объяснением?
- Стороны треугольника соответственно равны 4 см, 7 см и 9 см?
- Стороны треугольника соответственно равны 4 см, 7 см и 9 см?
- В прямоугольном треугольнике гипотенуза равна 15 см а катеты 9 см 12 см Найдите а)косинус большего острого угла б)сумму косинусов острых углов?
- В прямоугольном треугольнике гипотенуза равна 15 см, а катеты 9см и 12 см?
- Стороны треугольника соответственно равны 6 см, 9 см и 10 см?
- В прямоугольном треугольнике гипотенуза равна 15 см, а катеты — 9 см и 12 см?
- ПОМОГИТЕ ПОЖАЛУЙСТАоснование равнобедренного треугольника равно 6 см, а боковая сторона 5 см?
- Найдите косинус наименьшего угла треугольника, стороны которого равны 40 см, 70 см, 95 см?
- Длины сторон треугольника равны 3, 5, 6?
- Стороны прямоугольника равны 3 см и 4 см Найдите косинусы углов которыми образует диагональ со сторонами прямоугольника?
- Калькулятор и таблица для вычисления синуса и косинуса.
- Калькулятор для вычисления синуса и косинуса
- Синус острого угла прямоугольного треугольника.
- Косинус острого угла прямоугольного треугольника.
Видео:8 класс, 29 урок, Синус, косинус и тангенс острого угла прямоугольного треугольникаСкачать

Синус, косинус и тангенс острого угла прямоугольного треугольника
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.
Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.
Острый угол — меньший 90 градусов.
Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин 🙂
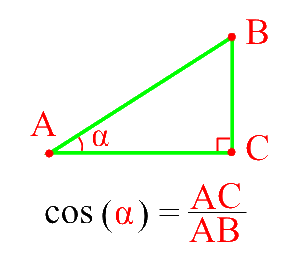
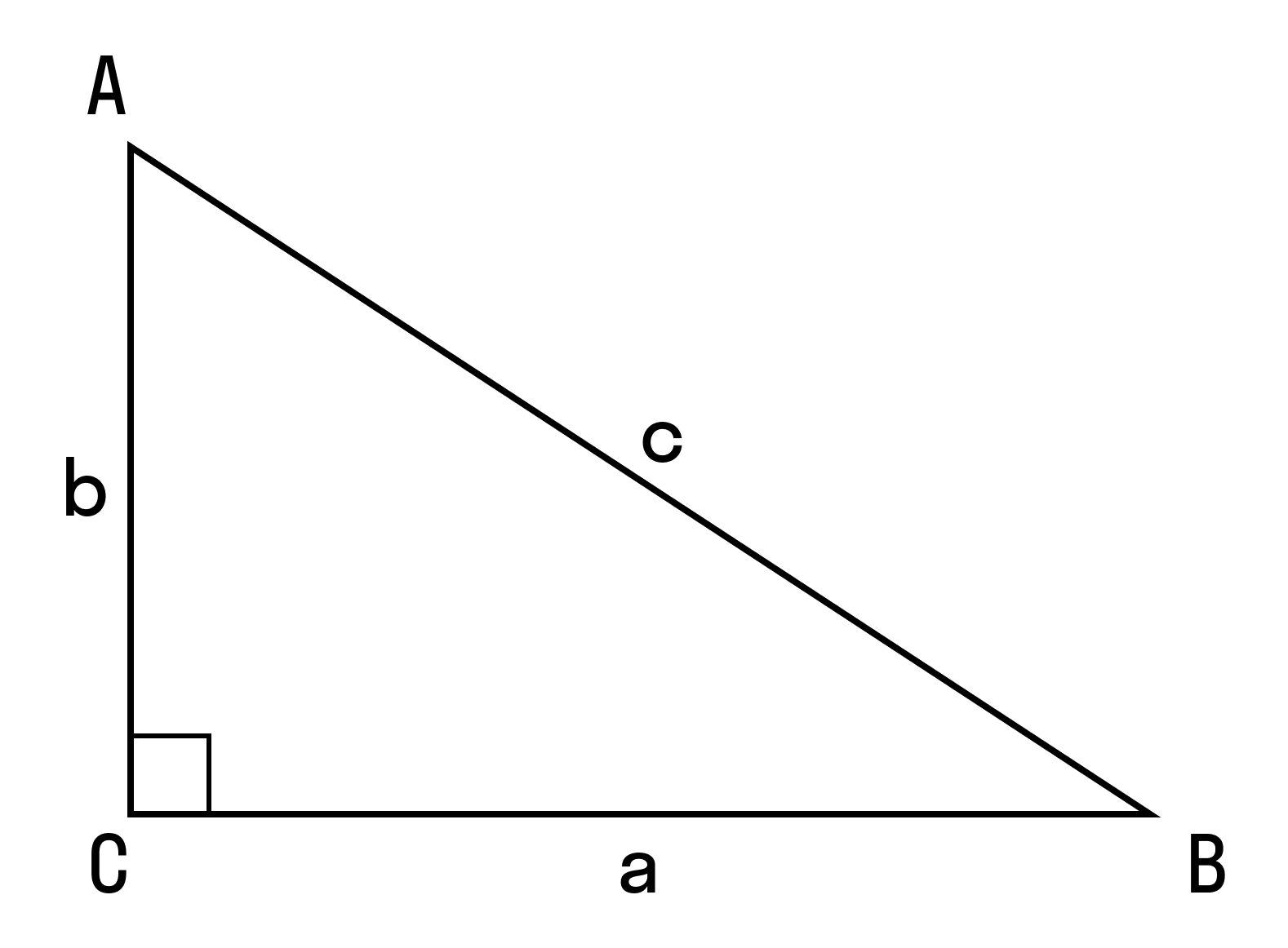
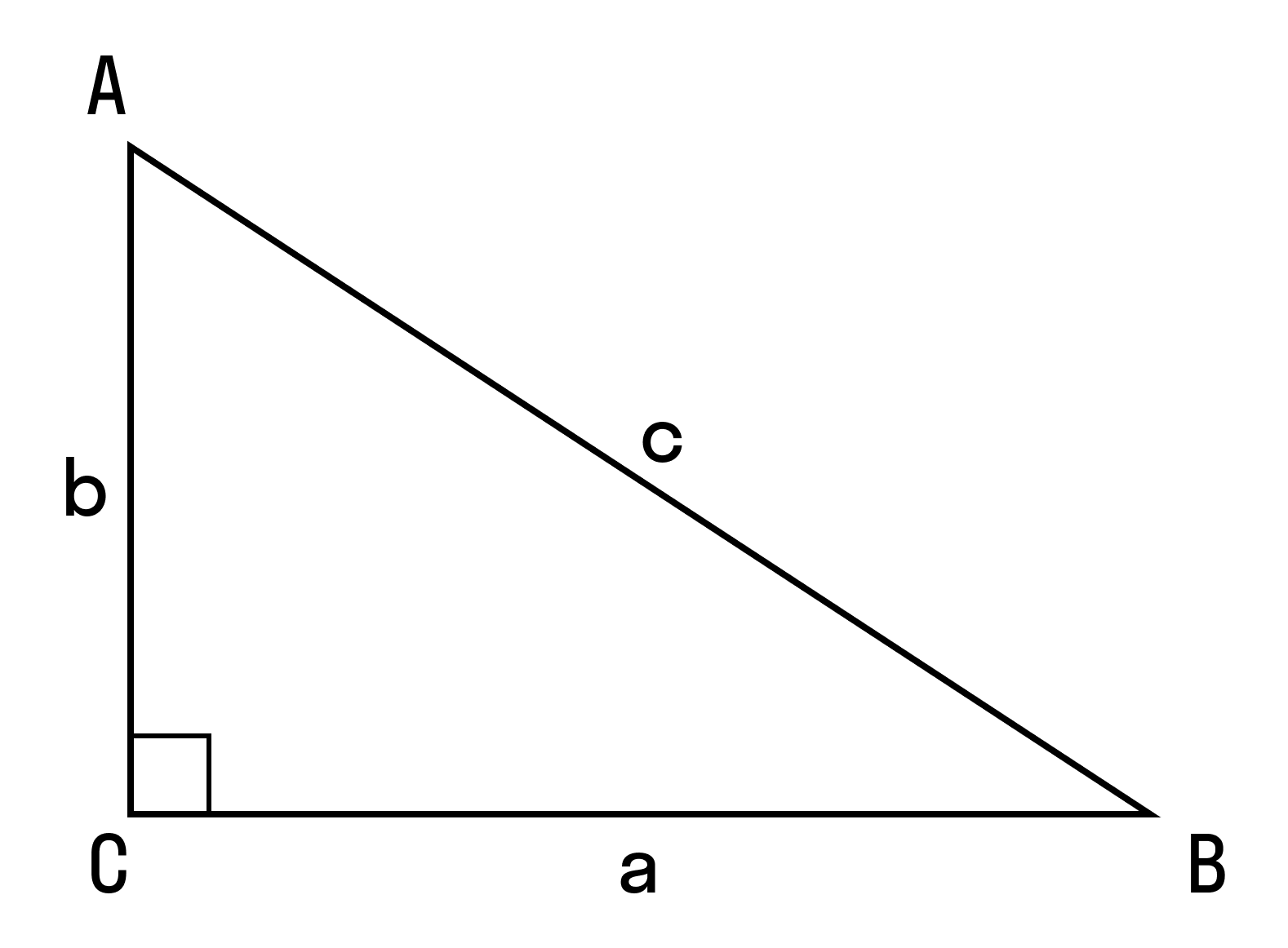
Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается . Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .
Угол обозначается соответствующей греческой буквой .
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Катет , лежащий напротив угла , называется противолежащим (по отношению к углу ). Другой катет , который лежит на одной из сторон угла , называется прилежащим.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.
Давайте докажем некоторые из них.
- Сумма углов любого треугольника равна . Значит, сумма двух острых углов прямоугольного треугольника равнa .
- С одной стороны, как отношение противолежащего катета к гипотенузе. С другой стороны, , поскольку для угла катет а будет прилежащим.Получаем, что . Иными словами, .
- Возьмем теорему Пифагора: . Поделим обе части на : Мы получили основное тригонометрическое тождество.
- Поделив обе части основного тригонометрического тождества на , получим: Это значит, что если нам дан тангенс острого угла , то мы сразу можем найти его косинус. Аналогично,
Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Мы знаем, что сумма углов любого треугольника равна .
Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?
С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от до .
| 0 | |
| 0 | |
| 0 | |
| 0 | − |
| − | 0 |
Обратите внимание на два красных прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.
Ты нашел то, что искал? Поделись с друзьями!
Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.
1. В треугольнике угол равен , . Найдите .
Задача решается за четыре секунды.
2 . В треугольнике угол равен , , . Найдите .
Найдем по теореме Пифагора.
Часто в задачах встречаются треугольники с углами и или с углами и . Основные соотношения для них запоминайте наизусть!
Для треугольника с углами и катет, лежащий напротив угла в , равен половине гипотенузы.
Треугольник с углами и — равнобедренный. В нем гипотенуза в раз больше катета.
Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.
Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Калькулятор и таблица для вычисления синуса и косинуса.
С помощью онлайн калькулятора вы сможете вычислить синус и косинус с точностью от одного до шестнадцати знаков после запятой. Чтобы вычислить синус и косинус, просто введите ваши данные.
Так же можно воспользоватся таблицей Брадиса синуса(sin) и косинуса(cos) от 0° до 360°.
Калькулятор для вычисления синуса и косинуса
Цифр после запятой
Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Синус острого угла прямоугольного треугольника.
Sin (α) острого угла прямоугольного треугольника — это отношение противолежащего катета(BC) к гипотенузе(AВ).
Пимер:
α = 40°; BC = 4,5см; AB = 7см.
sin (40°) = 4,5 7 = 0,6428
Видео:Теорема косинусов. Решить задачи. Найти сторону по двум сторонам и углу. Найти угол по сторонам.Скачать

Косинус острого угла прямоугольного треугольника.
Cos (α) острого угла прямоугольного треугольника — это отношение прилежащего катета(AC) к гипотенузе(AB).
Пимер:
α = 40°; AC = 6,98см; AB = 9см.
cos (40°) = 6,98 9 = 0,776
Видео:Как просто запомнить, что такое sin, cos, tg?! #косинус #синус #тангенс #математика #огэ #егэСкачать

Теорема косинусов и синусов
О чем эта статья:
Видео:9 класс, 15 урок, Решение треугольниковСкачать

Формулировка и доказательство теоремы косинусов
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Формула Теоремы Пифагора:
a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.
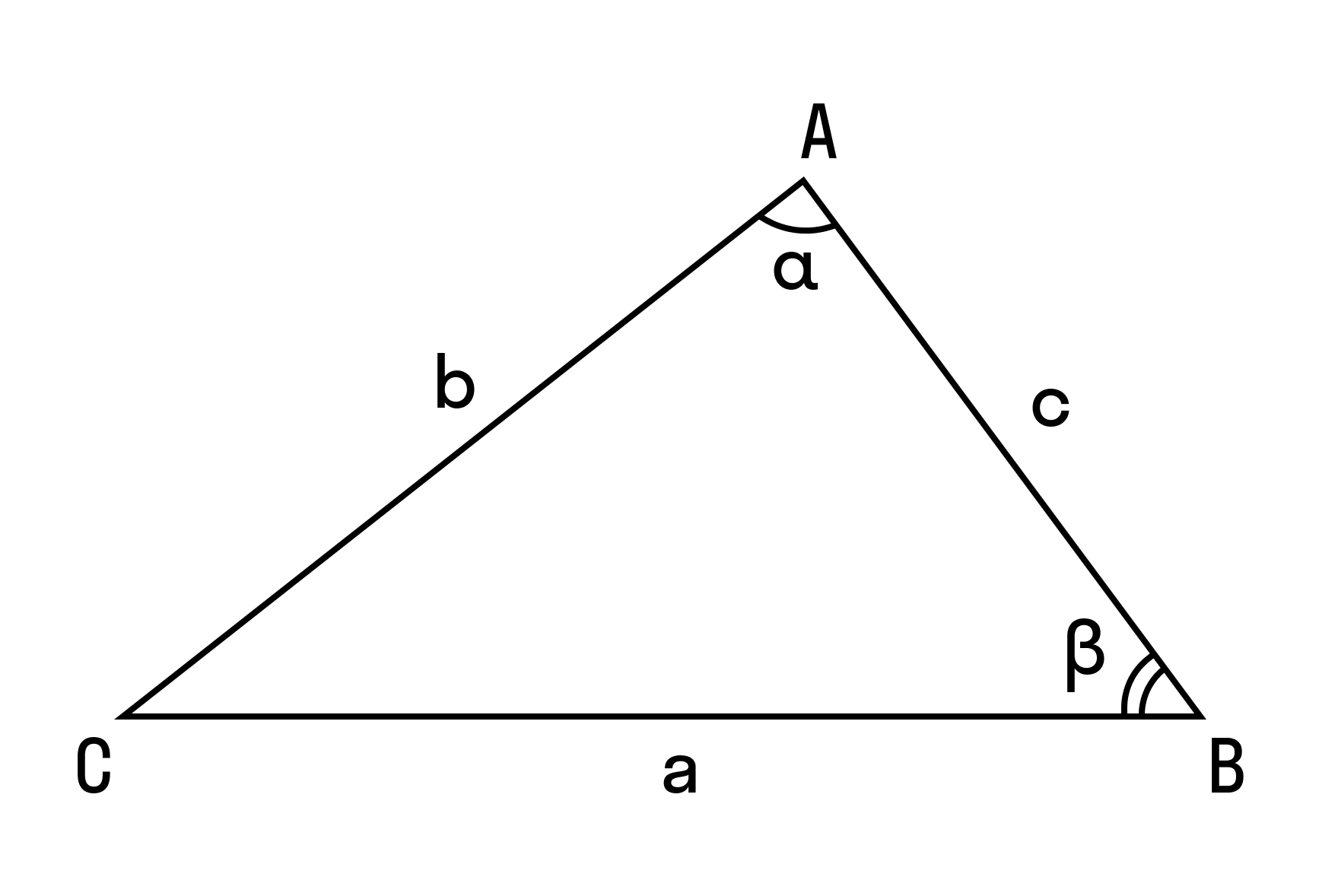
Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Формула теоремы косинусов:
a 2 = b 2 + c 2 — 2bc cos α
В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:
В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).
BC 2 = a 2 = (b cos α — c) 2 + b 2 sin 2 α = b 2 cos 2 α + b 2 sin 2 α — 2bc cos α + c 2 = b 2 (cos 2 α + sin 2 α) — 2bc cos α + c 2
cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.
Что и требовалось доказать.
Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.
С помощью теоремы косинусов можно найти косинус угла треугольника:
- Когда b 2 + c 2 — a 2 > 0, угол α будет острым.
- Когда b 2 + c 2 — a 2 = 0, угол α будет прямым.
- Когда b 2 + c 2 — a 2
Сформулируем еще одно доказательство теоремы косинусов.
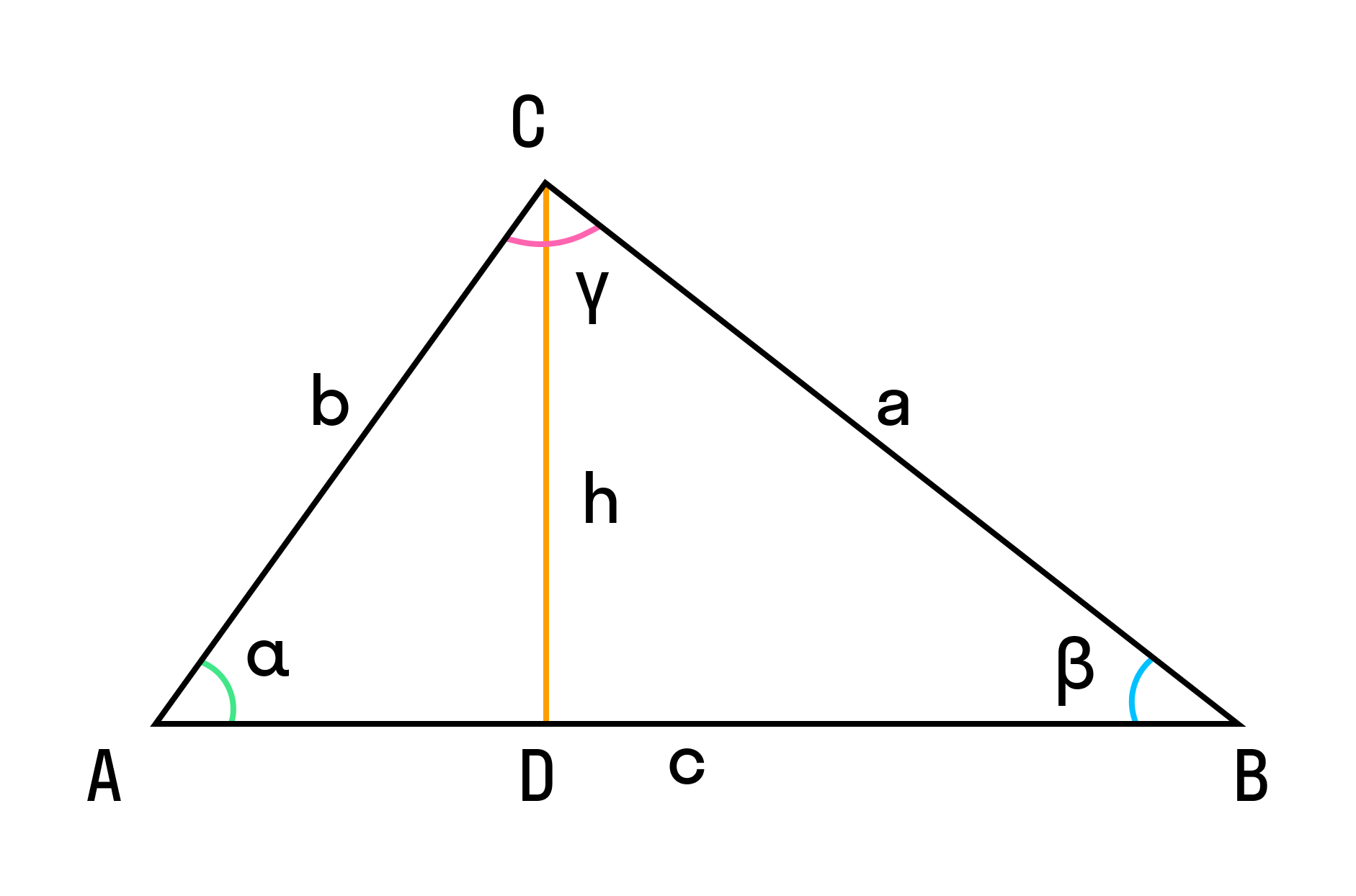
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:
- AD = b × cos α,
- DB = c – b × cos α.
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
- h 2 = b 2 — (b × cos α) 2
- h 2 = a 2 — (c – b × cos α) 2
Приравниваем правые части уравнений:
- b 2 — (b × cos α) 2 = a 2 — (c — b × cos α) 2
- a 2 = b 2 + c 2 — 2bc × cos α
Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определим стороны b и c:
- b 2 = a 2 + c 2 — 2ac × cos β;
- c 2 = a 2 + b 2 — 2ab × cos γ.
Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Формулировка теоремы для каждой из сторон треугольника
Теорема косинусов справедлива для всех сторон треугольника, то есть:
a 2 = b 2 + c 2 — 2bc cos α
b 2 = c 2 + a 2 — 2ca cos β
c 2 = a 2 + b 2 — 2ab cos γ
Теорема косинусов может быть использована для любого вида треугольника.
Видео:ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

Косинусы углов треугольника
Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:
Видео:7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

Определение угла с помощью косинуса
А теперь обратим внимание на углы.
Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).
Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.
Видео:Как найти значения синуса и косинуса, НЕ запоминая!Скачать

Рассмотрение пределов изменения cos α и sin α
Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.
Предел изменения косинуса: -1 0, то α ∈ (0°;90°)
Если cos α
Видео:Как запомнить значения синусов и косинусов?! #математика #синус #косинус #геометрия #егэ #shortsСкачать

Примеры решения задач
При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.
Пример 1. Дан треугольник АВС. Найти длину СМ.
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.
- Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B:
Из треугольника СМВ по теореме косинусов найдём СМ:
Пример 2. Дан треугольник АВС, в котором a2+ b22 + b 2 2 , то cos C 2 = a 2 + b 2 , то ∠C = 90°.
- Если c 2 2 + b 2 , то ∠C — острый.
Видео:КОСИНУС НА ПАЛЬЦАХ 🖐 #shorts #егэ #огэ #математика #профильныйегэСкачать

Найдите косинус меньшего угла треугольника, стороны которого 2 см 3 см 4смА)3 / 7 Б)3 / 8 В)5 / 8 Г)7 / 8 Д)5 / 7С объяснением?
Геометрия | 10 — 11 классы
Найдите косинус меньшего угла треугольника, стороны которого 2 см 3 см 4см
А)3 / 7 Б)3 / 8 В)5 / 8 Г)7 / 8 Д)5 / 7
Напротив меньшей стороны лежит меньший угол.
То есть надо найти косинус угла напротив стороны, равной 2.
Обозначим этот угол угломα.
Теорема косинусов : a² = b² + c² — 2bc * cosα
2² = 3² + 4² — 2 * 3 * 4 * cosα
4 = 9 + 16 — 24cosα
4 = 25 — 24cosα — 21 = — 24cosα
cosα = 21 / 24 = 7 / 8
Видео:Что такое синус, косинус и тангенс угла в прямоугольном треугольнике. Часть 1Скачать

Стороны треугольника соответственно равны 4 см, 7 см и 9 см?
Стороны треугольника соответственно равны 4 см, 7 см и 9 см.
Найди косинус большего угла треугольника.
Видео:№1048. Найдите косинусы углов треугольника с вершинами А (2; 8),Скачать

Стороны треугольника соответственно равны 4 см, 7 см и 9 см?
Стороны треугольника соответственно равны 4 см, 7 см и 9 см.
Найди косинус большего угла треугольника.
До сотых округлить.
Видео:ОГЭ по математике. В треугольнике АБС известно три стороны. Найди косинус угла. (Вар.8) √ 16Скачать

В прямоугольном треугольнике гипотенуза равна 15 см а катеты 9 см 12 см Найдите а)косинус большего острого угла б)сумму косинусов острых углов?
В прямоугольном треугольнике гипотенуза равна 15 см а катеты 9 см 12 см Найдите а)косинус большего острого угла б)сумму косинусов острых углов.
Видео:Определение синуса, косинуса и тангенса для любых углов от 0° до 180°. Геометрия 8-9 класс.Скачать

В прямоугольном треугольнике гипотенуза равна 15 см, а катеты 9см и 12 см?
В прямоугольном треугольнике гипотенуза равна 15 см, а катеты 9см и 12 см.
Найдите : а)косинус большего острого угла ; б)сумму косинусов острых углов.
Видео:ОГЭ 2020 задание 16Скачать

Стороны треугольника соответственно равны 6 см, 9 см и 10 см?
Стороны треугольника соответственно равны 6 см, 9 см и 10 см.
Найди косинус большего угла треугольника.
Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

В прямоугольном треугольнике гипотенуза равна 15 см, а катеты — 9 см и 12 см?
В прямоугольном треугольнике гипотенуза равна 15 см, а катеты — 9 см и 12 см.
Найдите : а) косинус большого острого угла ; б) сумму косинусов острых углов.
Видео:№256. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего из катетовСкачать

ПОМОГИТЕ ПОЖАЛУЙСТАоснование равнобедренного треугольника равно 6 см, а боковая сторона 5 см?
основание равнобедренного треугольника равно 6 см, а боковая сторона 5 см.
Найдите синус и косинус угла при основании треугольника.
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Найдите косинус наименьшего угла треугольника, стороны которого равны 40 см, 70 см, 95 см?
Найдите косинус наименьшего угла треугольника, стороны которого равны 40 см, 70 см, 95 см.
Длины сторон треугольника равны 3, 5, 6?
Длины сторон треугольника равны 3, 5, 6.
Найдите косинус наименьшего угла треугольника.
Стороны прямоугольника равны 3 см и 4 см Найдите косинусы углов которыми образует диагональ со сторонами прямоугольника?
Стороны прямоугольника равны 3 см и 4 см Найдите косинусы углов которыми образует диагональ со сторонами прямоугольника.
Вы перешли к вопросу Найдите косинус меньшего угла треугольника, стороны которого 2 см 3 см 4смА)3 / 7 Б)3 / 8 В)5 / 8 Г)7 / 8 Д)5 / 7С объяснением?. Он относится к категории Геометрия, для 10 — 11 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Геометрия. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.
Калькулятор и таблица для вычисления синуса и косинуса.
С помощью онлайн калькулятора вы сможете вычислить синус и косинус с точностью от одного до шестнадцати знаков после запятой. Чтобы вычислить синус и косинус, просто введите ваши данные.
Так же можно воспользоватся таблицей Брадиса синуса(sin) и косинуса(cos) от 0° до 360°.
Калькулятор для вычисления синуса и косинуса
Цифр после запятой
Синус острого угла прямоугольного треугольника.
Sin (α) острого угла прямоугольного треугольника — это отношение противолежащего катета(BC) к гипотенузе(AВ).
Пимер:
α = 40°; BC = 4,5см; AB = 7см.
sin (40°) = 4,5 7 = 0,6428
Косинус острого угла прямоугольного треугольника.
Cos (α) острого угла прямоугольного треугольника — это отношение прилежащего катета(AC) к гипотенузе(AB).
Пимер:
α = 40°; AC = 6,98см; AB = 9см.
cos (40°) = 6,98 9 = 0,776