Определить потенциал если заряд распределен по дуге окружности (8 видео)

Определить потенциал если заряд распределен по дуге окружности

2019-11-30
Заряд $q = 10^ к$ равномерно распределен по дуге окружности радиуса $R = 1 см$ с углом раствора а) $pi$ радиан, б) $2/3 pi$ радиан. Определите напряженность электрического поля в центре окружности.

а) Разобьем дугу на $n$ равных частей, каждая из которых имеет заряд $q/n$. При достаточно большом $n$ ($frac ll R$) эти заряды можно считать точечными. Каждый из зарядов создает в центре окружности поле с напряженностью $Delta vec_$, равной по величине

где $k = frac <4 pi epsilon_> = 9 cdot 10^ frac<нм^><к^>$. Направления векторов $Delta vec_$ показаны на рисунке а. Чтобы найти напряженность суммарного поля $vec = sum_^ Delta vec_$, будем последовательно складывать эти векторы, приставляя начало каждого из векторов к концу предыдущего (рис. б). Точность определения величины $vec$ тем выше, чем больше $n$.

Легко заметить, что при достаточно большом $n$ ломаную, которую образуют при сложении векторы $Delta vec_$, можно заменить полуокружностью, причем величина вектора $vec$ численно равна ее диаметру. Длина полуокружности $l$ равна

С другой стороны, $l = frac$. Отсюда

б) Задача для дуги с произвольным углом раствора $phi$ решается аналогично. В этом случае вектор $vec$ является хордой дуги окружности (рис. б). Длина дуги $l = n Delta E_$, центральный угол — $phi$ (рад) ($phi$ — максимальный угол между векторами $Delta vec_$).

Обозначим радиус окружности $r$ и выразим через него длину дуги $l$ и хорды $E$:

$l = r phi, E = 2r sin frac$.

Но $l = n Delta E_ = frac <R^>$, следовательно,

Содержание

Как написать реферат на отлично
По дуге окружности распределен заряд
По дуге окружности распределен заряд
По тонкой нити, изогнутой по дуге окружности радиусом R = 10 см, равномерно распределён заряд q = 20 нКл. Используя принцип суперпозиции, определите напряжённость электростатического поля E
Описание и исходные данные задания, 50% решения + фотография:
Электронная библиотека
📹 Видео

Видео:Физика 10 класс (Урок№27 - Напряжённость и потенциал электростатического поля.Разность потенциалов.)Скачать

Как написать реферат на отлично

По тонкой нити, изогнутой по дуге окружности радиусом R , равномерно распределен заряд с линейной плотностью t =10 нКл/м. Определить напряженность Е и потенциал j электрического поля, создаваемого таким распределенным зарядом в точке О, совпадающей с центром кривизны дуги. Длина l нити составляет 1/3 длины окружности и равна 15 см.

Решение. Выберем оси координат так, чтобы начало координат совпадало с центром кривизны дуги, а ось у была симметрично расположена относительно концов дуги (рис. 15.2). На нити выделим элемент длины dl . Заряд dQ = t dl , находящийся на выделенном участке, можно считать точечным.

Определим напряженность электрического поля в точке О. Для этого найдем сначала напряженность dE поля, создаваемого зарядом dQ :

где r —радиус-вектор, направленный от элемента dl к точке, напряженность в которой вычисляется. Выразим вектор dE через проекции dE_x c и dE_y на оси координат:

где i и j — единичные векторы направлений (орты).

[an error occurred while processing this directive]

Напряженность Е найдем интегрированием:

Интегрирование ведется вдоль дуги длины l . В силу симметрии интеграл равен нулю. Тогда

, (1)

где . Так как r = R = const и dl = R d J . то

Подставим найденное выражение dE_y в (1) и, приняв во внимание симметричное расположение дуги относительно оси Оу, пределы интегрирования возьмем от 0 до p /3, а результат удвоим;

Подставив указанные пределы и выразив R через длину дуги (3 l = 2 p r ), получим

Из этой формулы видно, что вектор Е совпадает с положительным направлением оси Оу Подставив значение t и l в последнюю формулу и сделав вычисления, найдем

Определим потенциал электрического поля в точке О. Найдем сначала потенциал d j , создаваемый точечным зарядом dQ в точке О:

Заменим r на R и произведем интегрирование:

.Так как l =2 p R /3, то

Произведя вычисления по этой формуле, получим

Видео:Задача №2. Потенциал проводящей сферы.Скачать

По дуге окружности распределен заряд

Видео:Поле заряженного кольцаСкачать

По дуге окружности распределен заряд

где $k = frac > = 9 cdot 10^ frac > >$. Направления векторов $Delta vec _$ показаны на рисунке а. Чтобы найти напряженность суммарного поля $vec = sum_ ^ Delta vec _$, будем последовательно складывать эти векторы, приставляя начало каждого из векторов к концу предыдущего (рис. б). Точность определения величины $vec $ тем выше, чем больше $n$.

Легко заметить, что при достаточно большом $n$ ломаную, которую образуют при сложении векторы $Delta vec _$, можно заменить полуокружностью, причем величина вектора $vec $ численно равна ее диаметру. Длина полуокружности $l$ равна

С другой стороны, $l = frac $. Отсюда

б) Задача для дуги с произвольным углом раствора $phi$ решается аналогично. В этом случае вектор $vec $ является хордой дуги окружности (рис. б). Длина дуги $l = n Delta E_$, центральный угол — $phi$ (рад) ($phi$ — максимальный угол между векторами $Delta vec _$).

Обозначим радиус окружности $r$ и выразим через него длину дуги $l$ и хорды $E$:

$l = r phi, E = 2r sin frac $.

Но $l = n Delta E_ = frac >$, следовательно,

Видео:Электрический потенциал - определение и решение простых задач.Скачать

По тонкой нити, изогнутой по дуге окружности радиусом R = 10 см, равномерно распределён заряд q = 20 нКл. Используя принцип суперпозиции, определите напряжённость электростатического поля E

Готовое решение: Заказ №8798

Тип работы: Задача

Статус: Выполнен (Зачтена преподавателем ВУЗа)

Предмет: Физика

Дата выполнения: 29.09.2020

Цена: 209 руб.

Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

№2 321. По тонкой нити, изогнутой по дуге окружности радиусом R = 10 см, равномерно распределён заряд q = 20 нКл. Используя принцип суперпозиции, определите напряжённость электростатического поля E, создаваемого этим зарядом в центре кривизны дуги, если длина нити равна четверти длины окружности.

Решение.

Четверть кольца радиуса имеет длину:

Определим линейную плотность заряда:

Рассмотрим элементарный участок четверти кольца.

Если вам нужно решить физику, тогда нажмите ➔ помощь по физике.

Похожие готовые решения:

Цепь состоит из катушки индуктивностью L = 0,1 Гн и источника тока. Источник тока отключили, не разрывая цепи. Время, через которое сила тока уменьшится до 0,001 первоначального значения
Поверхностная плотность заряда бесконечно протяжённой вертикальной плоскости равна 400 мкКл/м2. К плоскости на нити подвешен заряженный тяжёлый шарик массой m = 10 г. Определить заряд Q
Бесконечный тонкий прямой проводник равномерно заряжен с линейной плотностью заряда = 5•10-10 Кл/м. Считая, что на расстоянии r1 = 1 м от проводника потенциал созданного им электрического поля
Четверть тонкого кольца радиусом R = 10 см несёт равномерно распределённый заряд Q = 0,05 мкКл. Определить напряжённость E электрического поля, создаваемого распределённым зарядом в точке

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Лекция 2-2 Потенциал - примерыСкачать

Электронная библиотека

Пример 1. Расстояние (l) между двумя точечными зарядами Q₁ = 2 нКл и Q₂ = -3 нКл, расположенными в вакууме, равно 20 см. Определить: 1) напряженность ( ); 2) потенциал (j) поля, создаваемыми этими зарядами в точке, удаленной от первого заряда на расстоянии r₁ = 15 см и от второго заряда на r₂ = 10 см.

Определить: 1) ; 2) j.

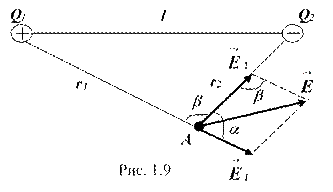
Решение. Согласно принципу суперпозиции имеем: (рис.1.9).

Напряженности электрического поля, создаваемые в вакууме зарядами Q₁ и Q₂ , равна:

Модуль вектора находится по теореме косинусов:

Подставив (1) и (3) в формулу (2), найдем искомую напряженность в точке А:

Согласно принципу суперпозиции, потенциал результирующего поля:

где и – соответственно потенциалы полей, создаваемых зарядами Q₁ и Q₂.

Подставив последние выражения в (4), найдем:

Вычисляя, получим: 1) = 3 кВ/м; 2) j = -150 В.

Пример 2. Электрическое поле создается бесконечно длинным цилиндром радиусом R = 7 мм, равномерно заряженным с линейной плотностью t = 15 нКл/м. Определить: 1) напряженность ( ) поля в точках, лежащих от оси цилиндра на расстояниях r₁ = 5 мм и r₂ = 1 см; 2) разность потенциалов между двумя точками этого поля, лежащими на расстоянии r₃ = 1 см и r₄ = 2 см от поверхности цилиндра, в средней его части.

Определить: 1) , ; 2) .

Решение. Воспользуемся теоремой Гаусса (1.1):

взяв в качестве замкнутой поверхности цилиндр, коаксиальный с заряженным, радиусом r и высотой l (рис. 1.10). Если r R

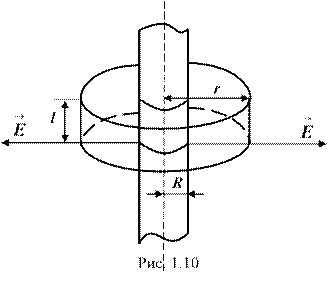
Так как , то полученная формула для поля с осевой симметрией запишется в виде:

Подставив сюда выражение для напряженности поля, создаваемого бесконечно длинным цилиндром , получим:

Проинтегрировав это выражение, найдем искомую разность потенциалов:

Вычисляя, получим: 1) = 0; = 27 кВ/м; 2) = 125 В.

Пример 3. Две концентрические проводящие сферы радиусами R₁ = 6 см и R₂ = 10 см несут соответственно заряды Q₁ = 1 нКл и Q₂ = -0,5 нКл. Найти напряженность ( ) поля в точках, находящихся от центра сфер на расстояниях: r₁ = 5 см, r₂ = 9 см, r₃ = 15 см. Построить график .

Решение. Заметим, что точки, в которых требуется найти напряженности электрического поля, лежат в трех областях (рис. 1.11): области I , области II , области III .

1) Для определения напряженности ( ) в области I проведем гауссову поверхность S₁ радиусом r₁ и воспользуемся теоремой Гаусса:

так как суммарный заряд, находящийся внутри гауссовой поверхности, равен нулю. Из соображений симметрии имеем: . Следовательно, и (напряженность поля в области I) во всех точках, удовлетворяющих условию , будет равна нулю.

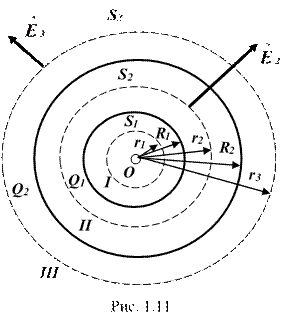
2) В области II гауссову поверхность проведем радиусом r₂.

так как внутри гауссовой поверхности находится только заряд Q₁.

Так как , то можно вынести за знак интеграла:

Обозначив напряженность для области II через , получим:

где – площадь гауссовой поверхности.

1) В области III гауссова поверхность проводится радиусом r₃. Обозначим напряженность области III через и учтем, что в этом случае гауссова поверхность охватывает обе сферы и, следовательно, суммарный заряд будет равен: . Тогда

Заметим, что ,поэтому это выражение можно переписать в виде:

Убедимся в том, что первая часть равенств (1) и (2) дает единицу напряженности:

Вычисляя, получим: = 0; = 1,11 кВ/м; = 200 В/м.

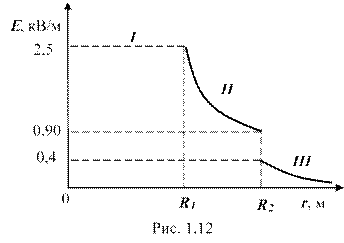
2) Построим график (рис. 1.12).

В области II изменяется по закону . В точке напряженность равна:

В области III изменяется по закону , причем в точке (r стремится к R₂ справа) и напряжённость равна: = 0,45 кВ/м.

Таким образом, функция в точках и терпит разрыв.

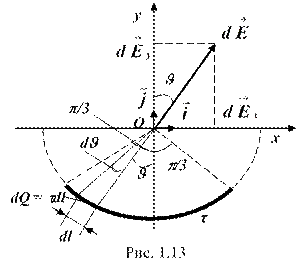
Пример 4. По тонкой нити, изогнутой по дуге окружности, равномерно распределен заряд с линейной плотностью t = 10 нКл/м. Определить напряженность ( ) и потенциал (j) электрического поля, создаваемого таким распределенным зарядом в точке, совпадающей с центром кривизны дуги. Длина (l) нити составляет 1/3 длины окружности и равна 15 см.

Дано: t = 10 нКл/м = 10×10 -9 Кл;

Решение. Выберем оси координат так, чтобы начало координат совпадало с центром кривизны дуги, а ось Oy была симметрично расположена относительно концов дуги (рис. 1.13). На нити выделим элемент длины dl. Заряд dQ = tdl, находящийся на выделенном участке, можно считать точечным.

Определим напряженность электрического поля в точке О. Для этого найдем сначала напряженность ( ) поля, создаваемого зарядом dQ:

где r – модуль радиуса-вектора, направленного от элемента dl к точке, в которой вычисляется напряженность.

Выразим вектор через проекции и на оси координат:

где и – единичные векторы направлений (орты).

Напряженность найдем интегрированием:

Интегрирование ведется вдоль дуги длиной l. В силу симметрии . Тогда

где . Так как , , то

Подставим выражение в (1) и, приняв во внимание симметричное расположение дуги относительно оси Oy, пределы интегрирования возьмем от 0 до p/3, а результат удвоим:

Из этой формулы видно, что напряженность поля по направлению совпадает с осью Oy.

Найдем потенциал электрического поля в точке О. Сначала найдем потенциал (dj), создаваемый точечным зарядом dQ в точке О:

Заменим r на R и проведем интегрирование:

Вычисляя, получим: = 2,18 кВ/м; j = 188 В.

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00