| Координаты центра первой окружности, через пробел |
| Радиус первой окружности |
| Координаты центра второй окружности, через пробел |
| Радиус второй окружности |
| Координата первого пересечения | ||||||||||||||||||||||
| Координата второго пересечения | ||||||||||||||||||||||
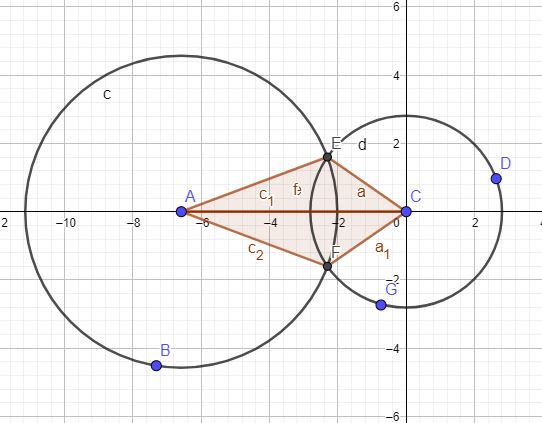
Продолжим изучение геометрии и в этом материале мы рассмотрим, как находить координаты пересечения двух окружностей, если заданы их уравнения. Определение координат двух окружностей на плоскости можно свести к более простым задачам которые мы можем уже решать или понимаем, как их решать. Пусть Две окружности заданы своими двумя уравнениями Повернем изображение на такой угол, что бы линия соединяющая центры окружностей, совпадала с осью абсцисс. Кроме этого перенесем всю схему таким образом, что бы центр одной из окружностей совпал с началом координат.
И алгоритм следующий: 1. Приводим ( линейным смещением) центр первой окружности к координатам (0,0) 3. Определяем угол (W) прямой, проходящей между точками A и C 4. Определяем два угла (psi_1) как сумму и (psi_2) как разность углов W и F 5. Взяв для каждого из углов (в п. 4), синус и умножив на радиус первой окружности мы узнаем координату Y , взяв косинус мы узнаем координату X. 6. Делаем для двух полученных координат, обратное смещение. Содержание
Видео:Алгоритмы. Пересечение окружностейСкачать  Пересечение двух окружностейЭтот онлайн калькулятор находит точки пересечения двух окружностей, если они существуют Чтобы использовать калькулятор, введите координаты x и y центра и радиус каждой окружности. Формулы для расчета приведены под калькулятором. Точки пересечения двух окружностейПервая окружностьВторая окружностьВидео:Взаимное расположение окружностей. Точки пересечения окружностейСкачать  Пересечение окружностейСама по себе задача нахождения точек пересечения двух окружностей достаточно проста, однако предварительно надо проанализировать если ли вообще точки пересения у данных двух окружностей. Поэтому начать надо с вычисления расстояния d в декартовых координатах между центрами окружностей и сравнения его с радиусами окружностей r1 и r2. При этом возможно следующие случаи (расстояние между центрами показано красным отрезком):
Если окружности действительно пересекаются, калькулятор использует следующие формулы (в-основном выведенные из теоремы Пифагора), проиллюстрированные рисунком ниже: Сначала калькулятор находит отрезок a Чтобы найти точку P3, калькулятор использует следующую формулу (в векторном виде): И наконец, чтобы найти точки пересечения, калькулятор использует следующие уравнения: Обратите внимание на разные знаки перед вторым слагаемым По теме также можно посмотреть следующие ссылки (на английском языке): Circle-Circle Intersection и Circles and spheres Видео:Определение точки пересечения окружности с прямойСкачать  Как найти пересекаются ли окружностиВидео:начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать  Пересечение двух окружностейЭтот онлайн калькулятор находит точки пересечения двух окружностей, если они существуют Чтобы использовать калькулятор, введите координаты x и y центра и радиус каждой окружности. Формулы для расчета приведены под калькулятором. Точки пересечения двух окружностейПервая окружностьВторая окружностьВидео:Найти центр и радиус окружностиСкачать  Пересечение окружностейСама по себе задача нахождения точек пересечения двух окружностей достаточно проста, однако предварительно надо проанализировать если ли вообще точки пересения у данных двух окружностей. Поэтому начать надо с вычисления расстояния d в декартовых координатах между центрами окружностей и сравнения его с радиусами окружностей r1 и r2. При этом возможно следующие случаи (расстояние между центрами показано красным отрезком):
Если окружности действительно пересекаются, калькулятор использует следующие формулы (в-основном выведенные из теоремы Пифагора), проиллюстрированные рисунком ниже: Сначала калькулятор находит отрезок a Чтобы найти точку P3, калькулятор использует следующую формулу (в векторном виде): И наконец, чтобы найти точки пересечения, калькулятор использует следующие уравнения: Обратите внимание на разные знаки перед вторым слагаемым По теме также можно посмотреть следующие ссылки (на английском языке): Circle-Circle Intersection и Circles and spheres Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать  Окружность. Относительное взаимоположение окружностей.Если две окружности имеют только одну общую точку, то говорят, что они касаются. Если же две окружности имеют две общие точки, то говорят, что они пересекаются. Трех общих точек две не сливающиеся окружности иметь не могут, потому, что в противном случае через три точки можно было бы провести две различные окружности, что невозможно. Будем называть линией центров прямую, проходящую через центры двух окружностей (например, прямую OO1). Теорема. Если две окружности имеют общую точку по одну сторону от линии центров, то они имеют общую точку и по другую сторону от этой линии, т.е. такие окружности пересекаются. Пусть окружности O и O1 имеют общую точку A, лежащую вне линии центров OO1. Требуется доказать, что эти окружности имеют еще общую точку по другую сторону от прямой OO1. Опустим из A на прямую OO1 перпендикуляр AB и продолжим его на расстояние BA1, равное AB. Докажем теперь, что точка A1 принадлежит обеим окружностям. Из построения видно, что точки O и O1 лежат на перпендикуляре, проведенном к отрезку AA1 через его середину. Из этого следует, что точка O одинаково удалена от A и A1. То же можно сказать и о точке O1. Значит обе окружности, при продолжении их, пройдут через A1.Таким образом, окружности имеют две общие точки : A (по условию) и A1 (по доказанному). Следовательно, они пересекаются. Следствие. Общая хорда (AA1) двух пересекающихся окружностей перпендикулярна к линии центров и делится ею пополам. Теоремы. 1. Если две окружности имеют общую точку на линии их центров или на ее продолжении, то они касаются. 2. Обратно: если две окружности касаются, то общая их точка лежит на линии центров или на ее продолжении. Признаки различных случаев относительного положения окружностей. Пусть имеем две окружности с центрами O и O1, радиусами R и R1 и расстоянием между центрами d. Эти окружности могут находиться в следующих 5-ти относительных положениях: 1. Окружности лежат одна вне другой, не касаясь. В этом случае, очевидно, d > R + R1 . 2. Окружности имеют внешнее касание. Тогда d = R + R1, так как точка касания лежит на линии центров O O1. 3. Окружности пересекаются. Тогда d R + R1, потому что в треугольнике OAO1 сторона OO1 меньше суммы, но больше разности двух других сторон. 4. Окружности имеют внутреннее касание. В этом случае в d = R — R1, потому что точка касания лежит на продолжении линии OO1. 5. Одна окружность лежит внутри другой, не касаясь. Тогда, очевидно, d R + R1, то окружности расположены одна вне другой, не касаясь. 2. Если d = R + R1, то окружности касаются извне. 3. Если d R — R1, то окружности пересекаются. 4. Если d = R — R1, то окружности касаются изнутри. 5. Если d R Е R1. Значит, все эти случаи исключаются. Остается один возможный, именно тот, который требовалось доказать. Таким образом, перечисленные признаки различных случаев относительно положения двух окружностей не только необходимы, но и достаточны. Видео:Как найти координаты точек на тригонометрической окружностиСкачать  Пересечение двух окружностейДаны две окружности, каждая определена координатами своего центра и радиусом. Требуется найти все их точки пересечения (либо одна, либо две, либо ни одной точки, либо окружности совпадают). Видео:Взаимное расположение и точки пересечения прямой и окружностиСкачать  РешениеПредположим, не теряя общности, что центр первой окружности — в начале координат (если это не так, то перенесём центр в начало координат, а при выводе ответа будем обратно прибавлять координаты центра). Тогда мы имеем систему двух уравнений: Вычтем из второго уравнения первое, чтобы избавиться от квадратов переменных: Таким образом, мы свели задачу о пересечении двух окружностей к задаче о пересечении первой окружности и следующей прямой: А решение последней задачи описано в соответствующей статье. Единственный вырожденный случай, который надо рассмотреть отдельно — когда центры окружностей совпадают. Действительно, в этом случае вместо уравнения прямой мы получим уравнение вида 0 = С, где C — некоторое число, и этот случай будет обрабатываться некорректно. Поэтому этот случай нужно рассмотреть отдельно: если радиусы окружностей совпадают, то ответ — бесконечность, иначе — точек пересечения нет. 🎬 ВидеоУравнение окружности ? Окружность в системе координат / Функция окружностиСкачать  8 класс. Найти координаты точек пересечения параболы с осями координатСкачать  Пересечение двух окружностейСкачать  Попадание точки в заданную область. Два сектора. Уроки программирования на С++.Скачать  Уравнение окружности (1)Скачать  №976. Найдите координаты точки пересечения прямых 4x + 3y-6 = 0 и 2х+у-4 = 0.Скачать  Точки пересечения графиков линейных функций. 7 класс.ОбразовательныйСкачать  10 класс, 11 урок, Числовая окружностьСкачать  Составляем уравнение прямой по точкамСкачать  Алгоритмы. Пересечение отрезков.Скачать  Пересечение двух окружностейСкачать  Всё про углы в окружности. Геометрия | МатематикаСкачать  |
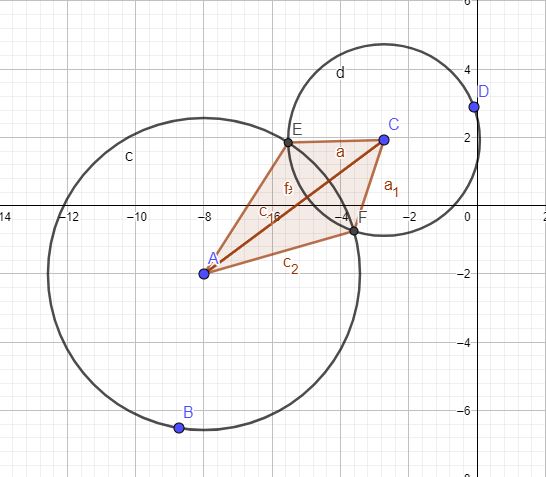
 Теперь мы можем решить данную задачу по несложной формуле.
Теперь мы можем решить данную задачу по несложной формуле.