Определение синуса и косинуса на единичной окружности самостоятельная работа (3 видео)

Определение синуса косинуса и тангенса угла
материал для подготовки к егэ (гиа) по алгебре (10 класс)

Самостоятельная работа на определение синуса, косинуса и тангенса угла и решение простейших тригонометрических уравнений.

Содержание

Скачать:
Предварительный просмотр:
По теме: методические разработки, презентации и конспекты
Дидактический материал по теме «Тригонометрия»
Содержимое разработки
Алгебра и начала математического анализа. 10 класс
💥 Видео

Видео:Синус, косинус произвольного угла. 9 класс.Скачать

Скачать:

Вложение	Размер
opredelenie_sinusa_kosinusa_i_tangensa_ugla.docx	68.71 КБ

Видео:ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

Предварительный просмотр:

Определение синуса косинуса и тангенса угла

Найти значение выражения (1-4):

Решить уравнение (8-12):

Определение синуса косинуса и тангенса угла

Найти значение выражения (1-4):

Решить уравнение (8-12):

Видео:Определение синуса и косинуса на единичной окружности | Алгебра 10 класс #11 | ИнфоурокСкачать

По теме: методические разработки, презентации и конспекты

Презентация к уроку по геометрии на тему: «Синус, косинус и тангенс угла»

Презентация к конспекту урока по геометрии на тему: «Синус, косинус и тангенс угла». тип урока: изучение нового материала. цель урока: ввести понятия синуса, косинуса и тангенса угла, актуализиро.

Конспект урока: «Синус, косинус и тангенс угла»

Урок подготовлен для учащихся 9 класса. Тип урока: изученик нового материала.

Синус,косинус и тангенс угла.

Конспект урока и презентация.

синус, косинус и тангенс угла

Ввести понятие синуса, косинуса и тангенса для углов от 0° до 180°; вывести основное тригонометрическое тождество и формулы для вычисления координат точки; рассмотреть формулы приведения .

Синус, косинус и тангенс угла

Изучение нового материала.

Технологическая карта урока Синус, косинус и тангенс угла

Синус, косинус и тангенс угла.

ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА (Определение синуса, косинуса и тангенса угла)

ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА по Алгебре 10 класс (Определение синуса, косинуса и тангенса угла).

Видео:Алгебра 10 класс (Урок№30 - Определение синуса, косинуса и тангенса угла.)Скачать

Дидактический материал по теме «Тригонометрия»

Самостоятельные работы и тест по теме «Тригонометрия»

Содержимое разработки

Государственное учреждение образования

«Средняя школа № 17 г. Могилева»

I квалификационной категории

Мог и лев 2016 г.

Градусная и радианная мера произвольных углов

Определение синуса, косинуса, тангенса и котангенса произвольного угла

Найдите координаты точки, полученной поворотом точки Р (1;0) на угол — .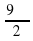

Отметьте на единичной окружности точку А_α, если:

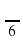
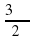
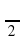
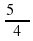
а) α =; б) α = ; в) α = 567 0 ; г) α = — ; д) α = ; е) α = — 1230 0 .

В какой четверти координатной плоскости расположена точка А_α, если α равно:

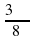
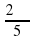
а) ; б) — ; в) 830 0 ; г) -1250 0 ; д) 1,8π; е) -2,3π.

На единичной окружности отметьте точку А_α (х; у), координаты которой удовлетворяют условию:

а) у = 0,5, х 0; б) х = 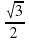, у 0.

Укажите три значения градусной меры угла α, при которых абсцисса соответствующей ему точки А_α равна:

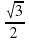
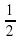
а) ; б) – 1; в) 0; г) — .

Градусная и радианная мера произвольных углов

Выразите в радианной мере величины углов:

а) 36 0 ; б) 216 0 ; в) 310 0 ; г) 360 0 ; д) 1021 0 .

Выразите в градусной мере величины углов:

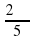
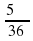
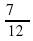
а) ; б) ; в) 5,3; г) — ; д) 11.

Определите в какой четверти оканчивается угол α, если его радианная мера равна:

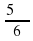
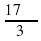
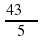
а) 9,1π; б) ; в) — ; г) -6,3π; д) — .

С помощью калькулятора или таблиц найдите:

а) радианные меры углов 17 0 ; 43 0 24 ‘ ; 83 0 36 ‘ ; 72 0 12 ‘ ;

б) градусные меры углов 0,384; 0,48; 1,11; 1,48.

а) Найдите радианную меру центрального угла сектора, если длина соответствующей дуги равна диаметру круга.

б) Длина дуги сектора втрое меньше его периметра. Найдите радианную меру его центрального угла.

Определение синуса, косинуса, тангенса и котангенса произвольного угла

Могут ли синус и косинус одного и того же угла быть равными соответственно:

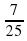
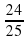
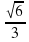
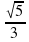
а) — и ; б) 0,4 и 0,7; в) и — .

Найдите числовое значение выражения:

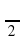
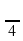
а ) sin 0 + cos + sin 2 ;

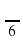
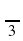
б ) 6 sin — 2 cos 0 + tg 2 ;

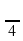
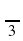
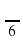
в ) 3 tg — sin 2 + cos 2 .

Отрицательным числом является:

а) cos 1300 0 ∙ sin 930 0 ∙ tg 185 0 ;

б ) cos 1230 0 ∙ sin 490 0 ∙ ctg 125 0 ;

в ) cos 1336 0 ∙ sin 691 0 ∙ tg 250 0 ;

г) cos 3600 0 ∙ sin 1290 0 ∙ ctg 250 0 .

Найдите значение выражения:

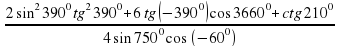
Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Алгебра и начала математического анализа. 10 класс

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок № 30. Определение синуса, косинуса и тангенса угла

Перечень вопросов, рассматриваемых в теме:

Ввод понятий синуса, косинуса, тангенса и котангенса угла
Определение синуса, косинуса, тангенса и котангенса угла
Решение простейших тригонометрических уравнений
Решение задач на применение знаний о синусе, косинусе, тангенсе и котангенсе в формате заданий ЕГЭ;

Глоссарий по теме

Синус угла– ордината точки, полученной поворотом точки (1; 0) вокруг начала координат на угол .

Обозначается

Косинус угла – абсцисса точки, полученной поворотом точки (1; 0) вокруг начала координат на угол .

Обозначается

Тангенс угла – отношение синуса угла к его косинусу.

Обозначается tg

Котангенс угла отношение косинуса угла к его синусу.

Обозначается сtg

На единичной окружности касательная, проведенная к точке (1; 0) называется линией тангенсов.

Касательная, проведенная к точке (0; 1) — линия котангенсов.

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

Зарождение тригонометрии относится к глубокой древности. Слово «тригонометрия» греческое: тригоно — треугольник, метрити — мера. Иными словами, тригонометрия — наука об измерении треугольников. Длительную историю имеет понятие синуса. Различные отношения отрезков треугольника и окружности встречаются уже в III в. до н. э. в работах великих математиков Древней Греции — Евклида, Архимеда, Аполлония Пергского. В IV—V вв. появился специальный термин в трудах по астрономии великого индийского ученого Ариабхаты (476 — ок.550). Отрезок он назвал ардхаджива, или более кратко джива. Арабскими математиками в IX в. слово джива было заменено на арабское слово джайб (выпуклость). При переводе арабских математических текстов в XII в. это слово было заменено латинским синус (sinus — изгиб, кривизна).

Косинус — это сокращение латинского выражения complementysinus, т. е. «дополнительный синус» или иначе «синус дополнительной дуги».

Название «тангенс» происходит от латинского tanger (касаться). Tangens переводится как «касающийся» (линия тангенсов — это касательная к единичной окружности).

Несмотря на то, что тригонометрия зародилась в древние времена, сегодня она охватывает практически все естественные науки и технику.

1.Найдите координаты точек А, В, С и D, лежащих на единичной окружности (рис. 1)

Рисунок 1 – единичная окружность

Поставьте в соответствие точке её координаты

Ответ: А(1; 0); В(0; 1); С(-1; 0); D(0; -1)

Сегодня на уроке мы узнаем, как по-другому называются абсцисса и ордината точки, лежащей на единичной окружности.

1.Рассмотрим окружность радиуса, равного 1 единичному отрезку, в прямоугольной системе координат хОу с центром в начале координат. Такую окружность называют

единичной или тригонометрической.

Рисунок 2 – точка Р на единичной окружности

Точка Р (1; 0) при повороте вокруг начала координат на угол переместилась в точку Рₐ. Определим её координаты. (рис. 2).

Синусом угла называется ордината точки, полученной поворотом точки (1; 0) вокруг начала координат на угол.

Обозначается

Косинусом угланазывается абсцисса точки, полученной поворотом точки (1; 0) вокруг начала координат на угол .

Обозначается

Угол может выражаться и в градусах и в радианах.

Точка А(1; 0) при повороте на угол 90 (рис. 1)

Ордината точки В равна 1, значит или

Абсцисса точки В равна 0, значит

Точка А(1; 0) при повороте на угол переместилась в точку ( рис. 1)

Найдите и

Ответ: = 0;

Точка А(1; 0) при повороте на угол переместилась в точку (рис. 1)

Найдите и

Ответ: =1= 0.

Рассмотрим ещё два понятия.

Определение. Тангенсом угла называется отношение синуса угла к его косинусу.

Обозначается tg

tg,

Найти tg 0. Вычислим по формуле tg = = 0.

Определение. Котангенсом угла называется отношение косинуса угла к его синусу.

Обозначается сtg

сtg

Найти сtg .

Вычислим по формуле сtg =

2. Меру угла(в радианах) можно рассматривать как действительное число, поэтому и – это числовые выражения. А так как каждая точка единичной окружности имеет координаты х и у такие, что выполняются неравенства -1 ≤ х ≤ 1; -1 ≤ у ≤ 1,то синус и косинус не могут превышать значения, больше .

Чтобы решить уравнения = а, нужно считать х неизвестным, число а – заданным.

Решить уравнение = 1.

Найдем точку с ординатой 1 и запишем, каким числам х она соответствует. На окружности мы видим эту точку: В (0; 1). Она соответствуют числу и всем числам вида

Решением уравнения = 1 являются х =.

3. Полезно знать синусы, косинусы, тангенсы некоторых углов. Для этого рассмотрим дугу единичной окружности в I четверти координатной плоскости (рис. 3).

Рисунок 3 – 1 четверть единичной окружности

Точки А (1; 0) и В (0; 1) нам знакомы. Рассмотрим ещё несколько точек на окружности и найдем их координаты. Точка С является серединой дуги АВ, значит угол АОС равен половине прямого угла, 45 или . Ордината точки С равна её абсциссе. Их значения нетрудно найти по теореме Пифагора из прямоугольного треугольника ОСF, оно равно А значит,

tg 45

Дуга АМ составляет третью часть прямого угла, . Ордината точки М равна , значит

, tg30.

Дуга АNсоставляет прямого угла, . Абсцисса точки N равна , поэтому

, tg 60.

Чтобы легче запомнить эти значения, придумали мнемоническое правило- правило на ладони (рис. 4).

Рисунок 4 — мнемоническое правило- правило на ладони

Расположим ладонь так, как на рисунке, пусть мизинцу соответствует угол 0, следующим пальцам– 30, 45, 60 и 90. Так же присвоим им номера: мизинец №0, следующие №1, №2, №3, №4. Чтобы найти синус, используем формулу: =. А для косинуса нумерацию будем вести от большого пальца, выполняя вычисления по той же формуле. =.

Например, =, = = .

А тангенс можно вычислить по формуле: tg = .

Тангенсы и котангенсы, также как и синусы, косинусы, можно определить по единичной окружности. Для этого познакомимся с ещё одним понятием.

На единичной окружности касательная, проведенная к точке (1; 0) называется линией тангенсов. Касательная, проведенная к точке (0; 1) — линия котангенсов (рис. 5).

Рисунок 5 – линия тангенсов и линия котангенсов

Например, чтобы найти tg, находим пересечение радиус-вектора под углом с линией тангеса. Это число , или .

Чтобы найти ctg , радиус-вектор под углом должен пересечь линию котангенсов.

Это число .

Примеры и разбор решения заданий тренировочного модуля

Решить уравнение =0.

Синусом угла является ордината точки, поэтому значения синусов находим по оси Оу.

Найдем точки А (1; 0) и С (-1; 0) с ординатой 0 и запишем, каким числам х они соответствуют. Они соответствуют числам 0 (точка А), (точка С), 2

Решением уравнения = 0 являются х =.

Z- множество целых чисел.

Решить уравнение=1.

Найдем точки с абсциссой 1 и запишем, каким числам х они соответствуют. На рис.3 мы видим эту точку: А (1; 0) Она соответствуют числу и всем числам вида