Окружности с центром о проведена касательная cd

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Ваш ответ

Видео:Урок 3. №23 ОГЭ. Касательная. Окружность с центром на стороне AC касается АВ в точке В.Скачать

решение вопроса

Видео:№641. Отрезки АВ и АС являются отрезками касательных к окружности с центром О, проведенными изСкачать

Похожие вопросы

• Все категории
• экономические 43,279
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,962
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CDСкачать

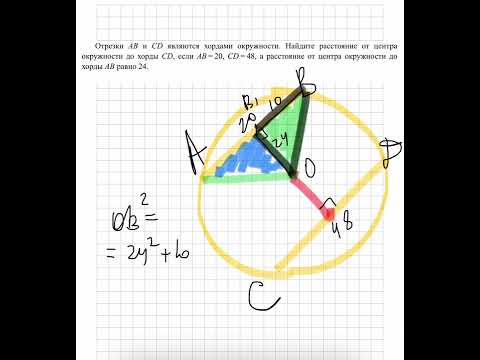
К окружности с центром о проведена касательная cd (d — точка касания) Найдите отрезок ОС если радиус окружности 6 см а угл DCO = 30?

Геометрия | 5 — 9 классы

К окружности с центром о проведена касательная cd (d — точка касания) Найдите отрезок ОС если радиус окружности 6 см а угл DCO = 30.

Мы достраиваем угол до треугольника получается радиус проведен в в точку касания.

Обозначим точку пересечения окружности и отрезка OC буквой M тогда по формуле CD квадрате = CM * CO.

Видео:К окружности с центром в точке O проведены ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Помогите, срочно?

Из точки А проведены две касательные к окружности с центром в точке О.

Найдите радиус окружности, если угол между касательными равен 60 градусов, а расстояние от точки А до точки О равно 6.

Видео:№676. Стороны угла А касаются окружности с центром О радиуса r. Найдите: а) ОА,Скачать

ВС — касательная к окружности с центром О(В — точка касания)?

ВС — касательная к окружности с центром О(В — точка касания).

Найдите СО, если ВС = 8см, а диаметр окружности равен 12см.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Через точку М , удаленную от центра окружности на 20 см , проведи касательная МК к ней (К — точка касания )?

Через точку М , удаленную от центра окружности на 20 см , проведи касательная МК к ней (К — точка касания ).

Радиус окружности равен 12см .

Вычеслите длину касательной МК

решение : проведеной радиус ок .

Видео:№640. Даны окружность с центром О радиуса 4,5 см и точка А. Через точку А проведены две касательныеСкачать

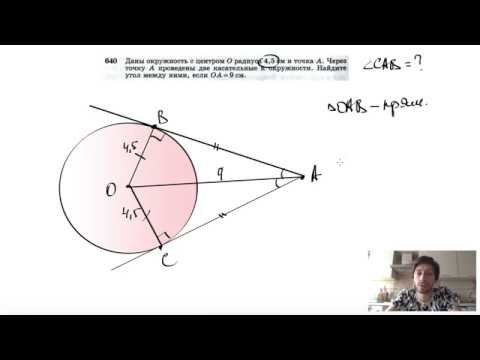
Из точки А проведены две касательные к окружности с центром в точке О?

Из точки А проведены две касательные к окружности с центром в точке О.

Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6.

Видео:№796. Из концов диаметра CD данной окружности проведены перпендикуляры СС1 и DD1 к касательнойСкачать

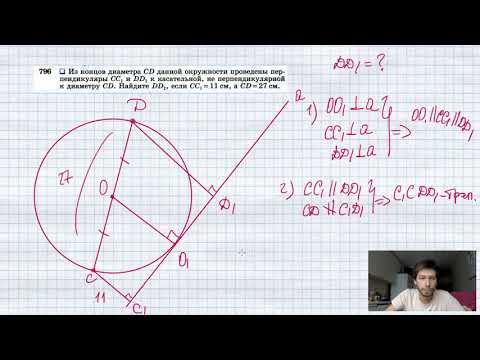
Из точки М проведены касательные MA и MB к окружности с центром в точке O (A и B — точки касания) найдите радиус окружности если угол AMB = a и AB = a?

Из точки М проведены касательные MA и MB к окружности с центром в точке O (A и B — точки касания) найдите радиус окружности если угол AMB = a и AB = a.

Видео:Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

К окружности с центром в точке О проведена касательная АК ( К — точка касания), домов отрезка АК равна √15?

К окружности с центром в точке О проведена касательная АК ( К — точка касания), домов отрезка АК равна √15.

Прямая АО пересекает окружность в точках В и С, причём АВ = 3.

Найдите диаметр окружности.

Видео:№643. Прямые АВ и АС касаются окружности с центром О в точках В и С. Найдите ВС, еслиСкачать

Из точки А, лежащей на окружности с центром в точке О, проведена касательная АS и секущая AR?

Из точки А, лежащей на окружности с центром в точке О, проведена касательная АS и секущая AR.

Найдите острый угол между касательной и секущей, если секущая равна радиусу окружности.

Видео:№145. Отрезок МК — диаметр окружности с центром О, а МР и РК — равные хорды этой окружностиСкачать

К окружности с центром О из точки А вне окружности проведены две касательные АВ и АС?

К окружности с центром О из точки А вне окружности проведены две касательные АВ и АС.

Отрезок, соединяющий точки касания, делит отрезок АО пополам.

Найдите угол ВАС.

Видео:Из точки С проведены две касательные к окружности с центром в точке ОСкачать

Из точки А к окружности с центром О проведены две касательные, К и Р — точки касания?

Из точки А к окружности с центром О проведены две касательные, К и Р — точки касания.

Известно, что угол КАР = 82°.

Найдите угол РОА.

Видео:Из точки A проведены две касательные к окружности с центром в точке O. Найдите радиус окружностиСкачать

К окружности с центром в точке О провели касательную CD(D — точка касания)?

К окружности с центром в точке О провели касательную CD(D — точка касания).

Найдите радиус окружности, если CO = 16см и уголCOD = 60градусов.

Видео:На отрезке AB выбрана точка C так, что AC=75 ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Из точки а к окружности с центром о проведена касательная ав найдите угол АО если радиус окружности 12 а угол АОВ = 45 ГРАДУСОВ?

Из точки а к окружности с центром о проведена касательная ав найдите угол АО если радиус окружности 12 а угол АОВ = 45 ГРАДУСОВ.

На этой странице сайта, в категории Геометрия размещен ответ на вопрос К окружности с центром о проведена касательная cd (d — точка касания) Найдите отрезок ОС если радиус окружности 6 см а угл DCO = 30?. По уровню сложности вопрос рассчитан на учащихся 5 — 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

2 = 2к + в — 1. 5 = 5. 5к + в — — — — — — — — — — — — — — — — 0. 5 = — 3. 5к| : ( — 3. 5) к = — 1 / 7 2 = 2 * ( — 1 / 7) + в в = 2 + (2 / 7) в = 2 + 2 / 7.

Угол между прямыми АВ1 и СD — это∠АB₁A₁ ( CD║A₁B₁) ΔAA₁B₁ AA₁ / A₁B₁ = tgα = √3, ⇒α = ∠АB₁A₁ = π / 3.

Второстепенными членами предложения бывают : 1) ОБСТОЯТЕЛЬСТВА, они могут отвечать на вопросы КОГДА? КАК ДОЛГО? (времени), ГДЕ? ОТКУДА? КУДА? (места), КАК? КАКИМ ОБРАЗОМ? (образа действия), ИЗ — ЗА ЧЕГО? ПОЧЕМУ? (причины), С КАКОЙ ЦЕЛЬЮ? ЗА..

Прилагательное , обстоятельство места (времени ), дополнение, еще есть причастные обороты (если знаешь, что это).

Имеем трапецию АВСД. Из вершин В и С опустим перпендикуляры ВЕ и СК на АД. Из равных треугольников АВе или СКД находим высоту трапеции по Пифагору : ВЕ = √(СД² — ((АД — ВС) / 2)²) = √(5² — 3²) = √(25 — 9) = √16 = 4. Средняя линия равна (10 + 4) / ..

1) треугольник NOM — р / б Угол ONM = углу OMN = (180° — 64°) : 2 = 58° Угол NMP = 90° Угол OMP = 90° — 58° = 32°.

A = 3 см b = 16 см c = 12 см V — ? V = abc = 3 * 16 * 12 = 576 (см³) Ответ : 576 см³.

Формула объёма для куба с ребром «a» : V = a * a * a = a ^ 3.

У куба шесть равных граней. 1) Полная поверхность куба по формуле Sполн = 6 * S = 6 * a² — ответ 2) Объем куба по формуле V = a³ — ответ.

Т. к а║b значит накрест лежащие углы равны х = 70°.

Видео:№1035. В окружности проведены хорды АВ и CD, пересекающиеся в точке Е. Найдите острыйСкачать

Касательная к окружности

О чем эта статья:

Видео:№146. Отрезки АВ и CD — диаметры окружности с центром О. Найдите периметр треугольника AOD, еслиСкачать

Касательная к окружности, секущая и хорда — в чем разница

В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.

Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.

Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).

Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой.

Видео:🔴 В окружности с центром O отрезки AC и BD ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

Свойства касательной к окружности

Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.

Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.

Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:

• окружность с центральной точкой А;
• прямая а — касательная к ней;
• радиус АВ, проведенный к касательной.

Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.

Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.

В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.

Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Задача

У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.

Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.

Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.

∠АОС = 180° — ∠САО — ∠АСО = 180° — 90° — 28° = 62°

Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, АВ = 62°.

Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.

Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.

Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°.

Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны.

Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.

Задача 1

У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.

Решение

Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.

∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).

Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:

∠BDC = ∠BDA × 2 = 30° × 2 = 60°

Итак, угол между касательными составляет 60°.

Задача 2

К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК.

Решение

Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.

Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.

∠МNК = (180° — ∠МКN) : 2 = (180° — 50°) : 2 = 65°

Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.

Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.

Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.

Задача 1

Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.

Решение

Исходя из соотношения касательной и секущей МА 2 = МВ × МС.

Найдем длину внешней части секущей:

МС = МВ — ВС = 16 — 12 = 4 (см)

МА 2 = МВ × МС = 16 х 4 = 64

Задача 2

Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.

Решение

Допустим, что МО = у, а радиус окружности обозначим как R.

В таком случае МВ = у + R, а МС = у – R.

Поскольку МВ = 2 МА, значит:

МА = МВ : 2 = (у + R) : 2

Согласно теореме о касательной и секущей, МА 2 = МВ × МС.

(у + R) 2 : 4 = (у + R) × (у — R)

Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:

Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).

Ответ: MO = 10 см.

Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.

Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.

Задача 1

Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.

Решение

Согласно свойствам угла между касательной и хордой, ∠АВС = ½ АВ.

АВ = ∠АВС × 2 = 32° × 2 = 64°

Задача 2

У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.

Решение

Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:

КМ = 2 ∠МКВ = 2 х 84° = 168°

Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.

∠ОКМ = ∠ОМК = (180° — ∠КОМ) : 2

Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:

∠ОМК = (180° — ∠КОМ) : 2 = (180° — 168°) : 2 = 6°

🔥 Видео

№639. Прямая АВ касается окружности с центром О радиуса r в точке В. Найдите АВСкачать

№638. Прямая АВ касается окружности с центром О радиуса r в точке В. Найдите АВСкачать