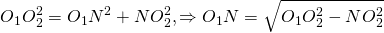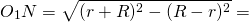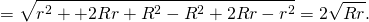Окружности радиусов 14 и 35 касаются внешним образом точки

Видео:ОГЭ. Понятный разбор задачи №26. Две окружности радиусов 44 и 77 касаются внешним образом...Скачать

Окружности радиусов 25 и 100 касаются внешним образом. Точки Аи В лежат на первой окружности, точки С и D — на второй. При этом АС и BD

Видео:Геометрия Окружности радиусов 25 и 100 касаются внешним образом. Точки A и B лежат на первой окружСкачать

Ваш ответ

Видео:Окружности касаются внешним образом #егэ2023 #математика #егэ #школа #shorts #fypСкачать

решение вопроса

Видео:ОГЭ № 25. "Окружности касаются внешним образом... "Скачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,937
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:ОГЭ по математике. 9 класс. Задача 26. Вариант 5.Скачать

Окружности касаются внешним образом

Окружности радиусов 44 и 77 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.

Соединим центры окружностей — точки O₁ и O₂ — с точками A и C соответственно.

Обозначим O₁A=r, O₂C=R.

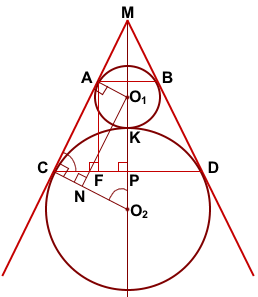
Проведём перпендикуляр AF к прямой CD и перпендикуляр O₁N к прямой CO₂.

AF — искомое расстояние между прямыми AB и CD.

Четырёхугольник AO₁NC — прямоугольник (так как у него три угла прямые).

Рассмотрим прямоугольный треугольник O₁O₂N.

Продлим касательные AC и BD до пересечения в точке M. Проведём луч MO₂.

Окружности с центрами в точках O₁ и O₂ вписаны в угол CMD, значит MP — биссектриса угла CMD.

MC=MD (как отрезки касательных, проведённых из одной точки). Значит треугольник CMD — равнобедренный с основанием CD. Следовательно, биссектриса MP является также его высотой.

В прямоугольном треугольнике CMP ∠MCP=90°-∠CMP.

В прямоугольном треугольнике CMO₂ ∠CO₂M=90°-∠CMP.

Отсюда ∠MCP=∠CO₂M. Следовательно, прямоугольные треугольники AFC и O₁NO₂ подобны (по острому углу).

Видео:Радиус и диаметрСкачать

Окружности радиусов 4 и 60 касаются внешним образом?

Геометрия | 5 — 9 классы

Окружности радиусов 4 и 60 касаются внешним образом.

Точки A и B лежат на первой окружности, точки C и D — на второй.

При это AC и BD — общие касательные окружностей.

Найдите расстояние между прямыми AB и CD.

АО1 = 4, СО2 = 60, Найти АР.

О1О2 = 4 + 60 = 64.

Тр — ки АСК и CHR подобны, так как∠К — общий и оба прямоугольные, значит АК / СК = СК / РК⇒ РК = СК² / АК.

СК = СО2 — КО2 = 60 — 4 = 56.

АР = АК — РК = 64 — 49 = 15 — это ответ.

Видео:ОГЭ Задание 26 Внешнее касание двух окружностейСкачать

Две окружности касаются друг друга внешним образом в точке M?

Две окружности касаются друг друга внешним образом в точке M.

Общая внешняя касательная к этим окружностям касается их в точках A и B, причем MA = 8 ; MB = 6.

Определите радиусы окружностей.

Видео:ОГЭ по математике. Задача 26Скачать

Окружность радиуса 2 внешне касается окружности меньшего радиуса?

Окружность радиуса 2 внешне касается окружности меньшего радиуса.

К этим окружностям проведена общая касательная, расстояние между точками касания равно 3.

Найдите радиус меньшей окружности.

Видео:Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать

Окружности радиусов 3 и 6 с центрами соответственно в точках и O1 и O2 касаются внешним образом в точке A?

Окружности радиусов 3 и 6 с центрами соответственно в точках и O1 и O2 касаются внешним образом в точке A.

К окружностям проведены общая внешняя касательная и общая внутренняя касательная.

Эти касательные пересекаются в точке B, а L — общая точка внешней касательной и окружности радиуса 3.

Найдите R радиус окружности, вписанной в четырёхугольник ABLO2.

В ответ записать R(корень из 2 + 1).

Видео:Две окружности разных радиусов касаются внешним образом в точке КСкачать

Две окружности с радиусами 5 и 3 касаются в точке О?

Две окружности с радиусами 5 и 3 касаются в точке О.

Их общая касательная, проходящая через точку О, пересекает внешние касательные этих окружностей в точках А и В соответственно.

Видео:Две касающиеся внешним образом в точке А окружности, радиусы которых равны 4 и 8Скачать

Две касающихся внешним образом в точке К окружности, радиусы которых = 6и24, вписаны в угол с вершиной А?

Две касающихся внешним образом в точке К окружности, радиусы которых = 6и24, вписаны в угол с вершиной А.

Общая касательная к этим окружностям, проходящая через точку К, пересекает стороны угла в точках В и С, Найдите радиус окружности, описанной около треугольника АВС.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

2 окружности радиусы которых 4 и 6 , касаются внешним образом, их общие внешние касательные пересекаются в точке М найдите расстояние до центра меньшей из окружностей?

2 окружности радиусы которых 4 и 6 , касаются внешним образом, их общие внешние касательные пересекаются в точке М найдите расстояние до центра меньшей из окружностей.

Видео:Задание 26 Две окружности, внешнее касаниеСкачать

Две окружности касаются внешним образом в точке К?

Две окружности касаются внешним образом в точке К.

Прямая касается первой окружности в точке А, а второй – в точке В.

Прямая ВК пересекает первую окружность в точке D, прямая АК пересекает вторую окружность в точке С.

А) Докажите, что прямые AD и BC параллельны.

Б) Найдите площадь треугольника DКС, если известно, что радиусы окружностей равны 1 и 4.

Видео:две окружности касаются внешним образом в точке КСкачать

Окружность радиуса 4 касается внешним образом второй окружности в точке B общая касательная к этим окружностям проходящая через точку B пересекаются с некоторой другой их общей касательной в точке A н?

Окружность радиуса 4 касается внешним образом второй окружности в точке B общая касательная к этим окружностям проходящая через точку B пересекаются с некоторой другой их общей касательной в точке A найдите радиус окружности если AB равно 6.

Видео:Разбор 3 варианта из сборника Ященко. Зонты | Математика ОГЭ 2023 | УмскулСкачать

Две окружности радиусами R и r касаются внешним образом в точке M?

Две окружности радиусами R и r касаются внешним образом в точке M.

К окружностям проведена общая внешняя касательная NK, где N и K — точки касания.

В криволенейный треугольник MNK вписана окружность.

Найдите ее радиус.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Окружности с радиусамии 6 и 2 касаются внешне?

Окружности с радиусамии 6 и 2 касаются внешне.

Найдите расстояние от точки касания до общей касательной к окружностям.

Перед вами страница с вопросом Окружности радиусов 4 и 60 касаются внешним образом?, который относится к категории Геометрия. Уровень сложности соответствует учебной программе для учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.

Равны по 1 признаку равенства (2 стороны и цгол между ними0.

Наверное на 4 (но я не уверена) лучше подождать следующего ответа.

∡ABF = 80° — — — > ∡ABC = 180° — 80° = 100° ∡BAC = ∡BCA = (180° — 100°) / 2 = 40° ∡OAC = ∡OCA = 40° / 2 = 20° ∡AOC = 180° — 20° — 20° = 140°.

8 + 4 — 6 = 6(см) — — — сторона CD.

Получается AB — гипотенуза. По теореме Пифагора считаем : AB² = AC² + BC² AB² = 7² + 24² AB² = 49 + 576 AB² = 625 AB = √625 AB = 25 Квадратный корень — это произведение числа на самое себя. √625можно вычислить так : √625 = √25 * 25 = √25 * √25 = 5 ..

∠АМВ = ∠DAM = 16° как накрест лежащие при пересечении параллельных прямых AD и ВС секущей АМ, ∠BAD = 2∠DAM = 2 · 16° = 32° так как АМ — биссектриса.

80 и 100 ? X + 20 + x = 180 x = 80.

BM медиана треугольника АВС.

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны називаєтса медиана.

Видео:Геометрия Две окружности радиусом R = 3 см и r = 1 см касаются внешним образом. Найти расстояние отСкачать

Окружности касаются внешним образом

Окружности радиусов 44 и 77 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.

Соединим центры окружностей — точки O₁ и O₂ — с точками A и C соответственно.

Обозначим O₁A=r, O₂C=R.

Проведём перпендикуляр AF к прямой CD и перпендикуляр O₁N к прямой CO₂.

AF — искомое расстояние между прямыми AB и CD.

Четырёхугольник AO₁NC — прямоугольник (так как у него три угла прямые).

Рассмотрим прямоугольный треугольник O₁O₂N.

Продлим касательные AC и BD до пересечения в точке M. Проведём луч MO₂.

Окружности с центрами в точках O₁ и O₂ вписаны в угол CMD, значит MP — биссектриса угла CMD.

MC=MD (как отрезки касательных, проведённых из одной точки). Значит треугольник CMD — равнобедренный с основанием CD. Следовательно, биссектриса MP является также его высотой.

В прямоугольном треугольнике CMP ∠MCP=90°-∠CMP.

В прямоугольном треугольнике CMO₂ ∠CO₂M=90°-∠CMP.

Отсюда ∠MCP=∠CO₂M. Следовательно, прямоугольные треугольники AFC и O₁NO₂ подобны (по острому углу).

Видео:Задание 26 Две окружности, вписанные в угол Внешнее касаниеСкачать

Решение №2523 Окружности радиусов 25 и 100 касаются внешним образом. Точки А и В лежат на первой окружности, точки С и D …

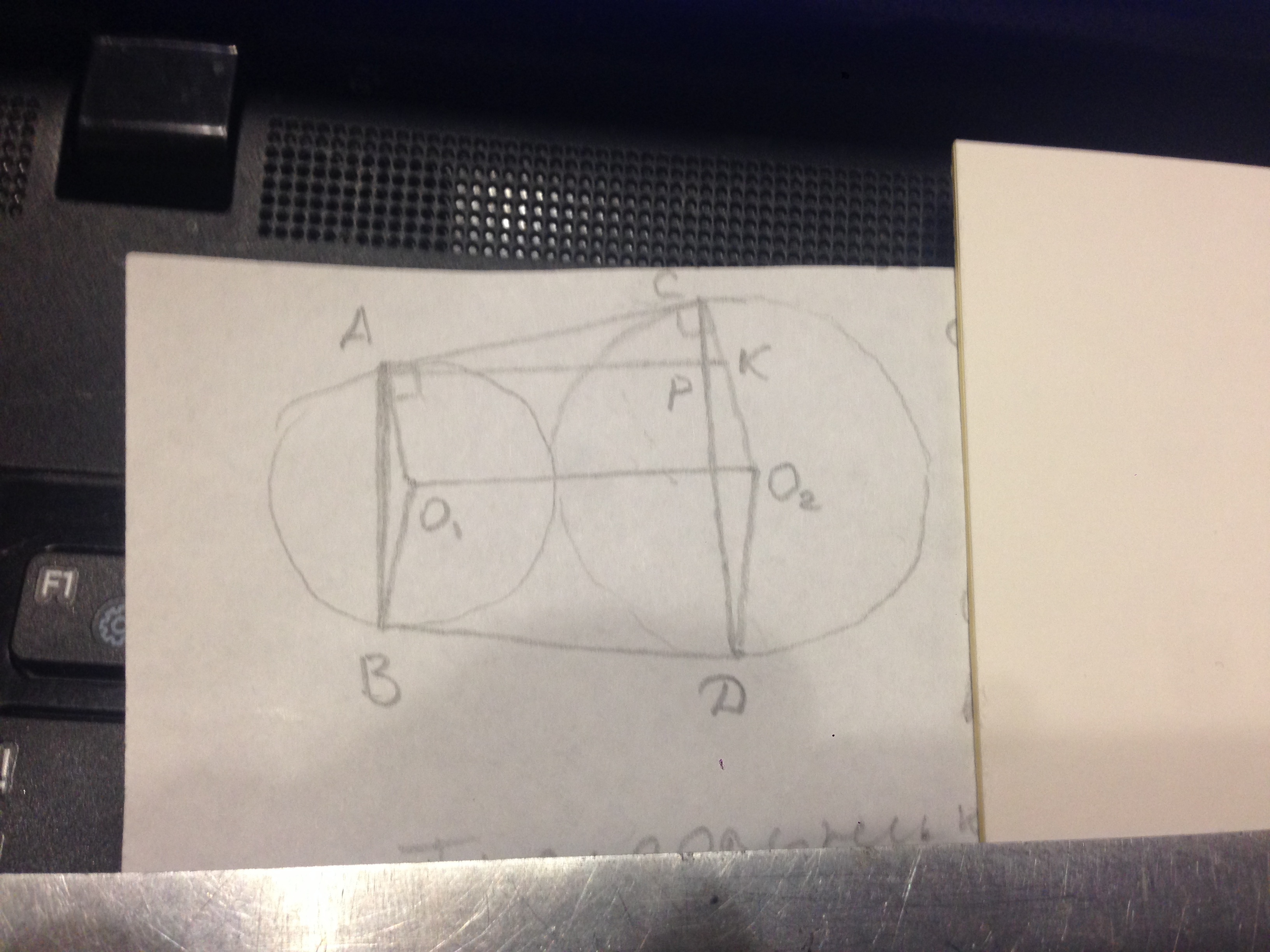
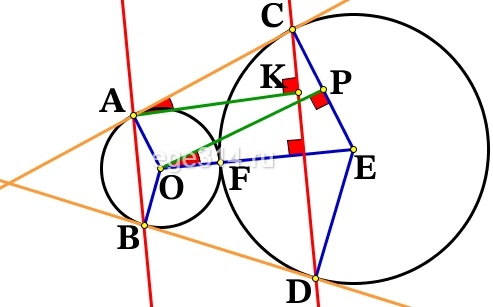
Окружности радиусов 25 и 100 касаются внешним образом. Точки А и В лежат на первой окружности, точки С и D – на второй. При этом АС и ВD – общие касательные окружностей. Найдите расстояние между прямыми АВ и СD.

Источник: ОГЭ Ященко 2022 (50 вар)

Построим рисунок по условию, + проведём радиусы: ОA , ОF , OB , EF , EC , ED , построим перпендикуляры AK ⊥ CD , OP ⊥ EC :

AK – искомое расстояние между прямыми АВ и CD .
ΔCAK∼ΔPOE, по двум равным углам (∠CKA=∠OPE = 90°, ∠CAK = ∠POE, т.к. АС||OP, AK||OE). Запишем соотношение сторон:

Выразим АК :

Найдём ОЕ, как сумму двух радиусов:

OE = OF + EF = 25 + 100 = 125

AOPC – прямоугольник (EC⊥AC, OA⊥AC, как радиусы и касательная), противоположные стороны равны:

ОА = РС = 25
АС = ОР

Найдём EP, как разность двух радиусов:

EP = EC – PC = EC – OA = 100 – 25 = 75

В прямоугольном ΔОРЕ по теореме Пифагора найдём ОР :

ОР 2 = ОE 2 – EP 2 = 125 2 – 75 2 = (125 – 75)·(125 + 75) = 50·200 = 10000

Найдём искомое расстояние АК :

📹 Видео

Профильный ЕГЭ 2024. Задача 16. Касающиеся окружностиСкачать

✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать