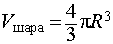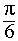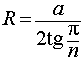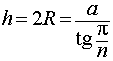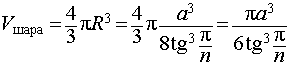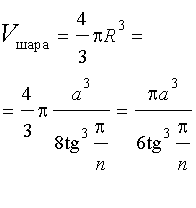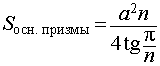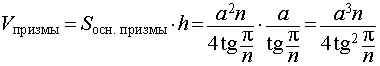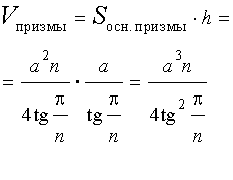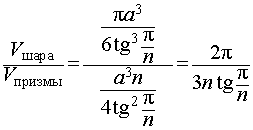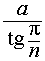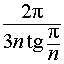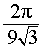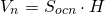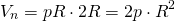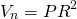Сфера, вписанная в призму. Свойства прямой призмы, описанной около сферы Сфера, вписанная в призму. Свойства прямой призмы, описанной около сферы |
 Отношение объемов шара и куба, описанного около сферы, ограничивающей этот шар Отношение объемов шара и куба, описанного около сферы, ограничивающей этот шар |
 Свойства правильной призмы, описанной около сферы. Отношение объемов шара и правильной n — угольной призмы, описанной около сферы, ограничивающей этот шар Свойства правильной призмы, описанной около сферы. Отношение объемов шара и правильной n — угольной призмы, описанной около сферы, ограничивающей этот шар |
- Сфера, вписанная в призму. Свойства прямой призмы, описанной около сферы
- Отношение объемов шара и куба, описанного около сферы, ограничивающей этот шар
- Свойства правильной призмы, описанной около сферы. Отношение объемов шара и правильной n — угольной призмы, описанной около сферы, ограничивающей этот шар
- Узнать ещё
- Шар, вписанный в призму
- Призма
- Призма
- Формулы вычисления объема и площади поверхности призмы:
- В основании лежит треугольник.
- В основании лежит четырехугольник
- 1. Прямоугольник
- 2. Ромб
- 3. Трапеция
- Рассмотрим площади правильных многоугольников:
- Подобие треугольников
- Прямоугольный треугольник и его свойства:
- Теорема Пифагора
- Теорема синусов
- Теорема косинусов
- 📽️ Видео
Видео:Призма и цилиндр. Практическая часть. 11 класс.Скачать

Сфера, вписанная в призму. Свойства прямой призмы, описанной около сферы
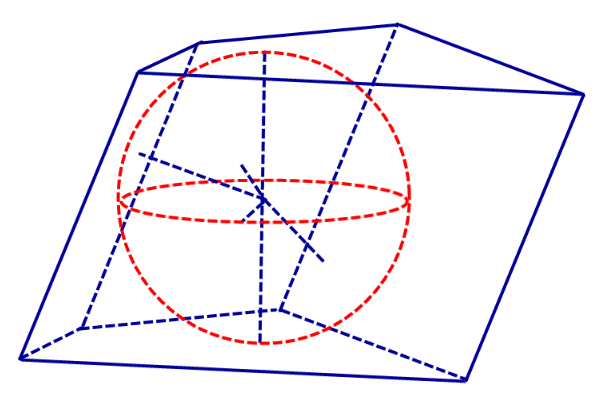
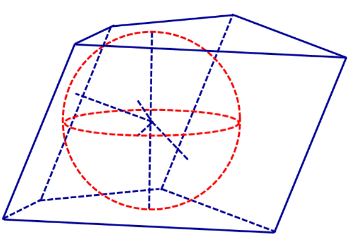
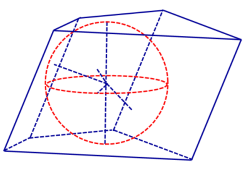
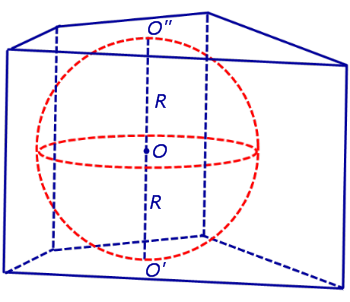
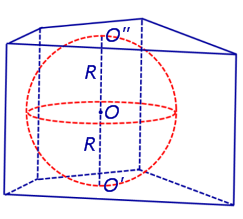
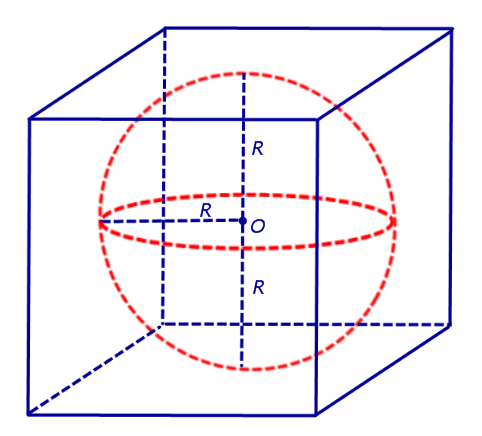
Определение 1. Сферой, вписанной в призму, называют такую сферу, которая касается плоскостей всех граней призмы, причем точки касания лежат на гранях призмы (рис. 1).
Определение 2. Если сфера вписана в призму, то призму называют описанной около сферы.
Таким образом, если призма описана около сферы, то плоскости всех граней призмы являются касательными плоскостями к этой сфере.
Далее мы будем рассматривать только прямые призмы.
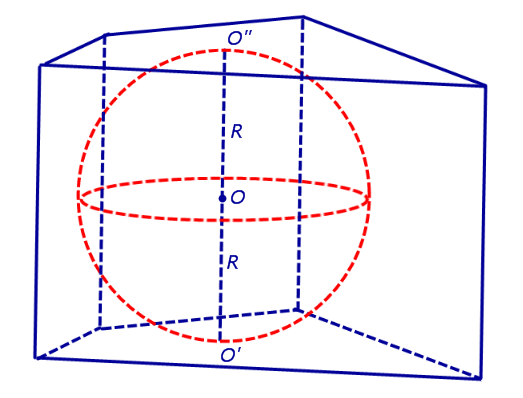
Утверждение. Если в прямую призму вписана сфера радиуса R , то высота призмы равна 2R , а в основания призмы можно вписать окружности радиуса R .
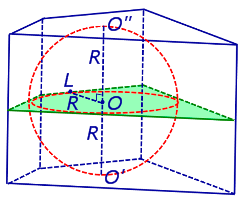
Обозначим буквой O центр вписанной сферы, а символами O’ и O» – точки касания сферы с плоскостями оснований призмы. Заметим, что плоскости оснований призмы параллельны, а радиусы OO’ и OO» проведены в точки касания сферы с плоскостями оснований призмы и, следовательно, перпендикулярны плоскостям оснований призмы. Поэтому прямая O’O» перпендикулярна плоскостям оснований призмы, центр вписанной сферы O является серединой отрезка O’O» , а высота призмы равна длине отрезка O’O» и равна 2R .
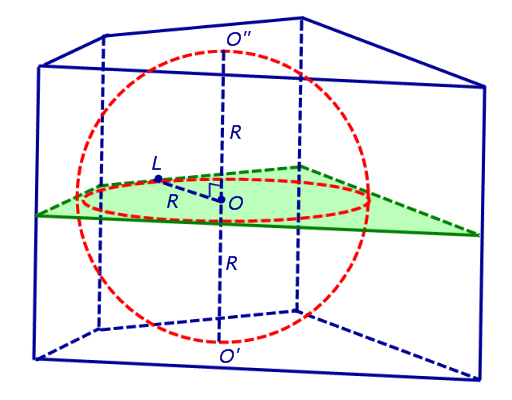
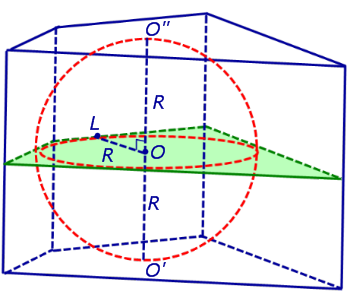
Проведем через точку O плоскость, перпендикулярную прямой O’O» , и докажем, что все точки касания сферы с боковыми гранями призмы лежат в этой плоскости. Для этого обозначим точку касания сферы с какой-либо гранью призмы буквой L и докажем, что прямая OL перпендикулярна прямой O’O» (рис. 3).
Действительно, радиус OL , проведенный в точку касания сферы с боковой гранью призмы перпендикулярен плоскости этой грани, а, значит, перпендикулярен любой прямой, лежащей на этой грани, и, в том числе, OL будет перпендикулярен боковому ребру призмы.
Рассматриваемая призма является прямой призмой, поэтому ее боковые ребра перпендикулярны к плоскостям оснований. Прямая O’O» также перпендикулярна к плоскостям оснований и, следовательно, параллельна боковым ребрам призмы. следовательно, параллельна боковым ребрам призмы. Таким образом, мы можем заключить, что прямая OL перпендикулярна прямой O’O» и, значит, лежит в плоскости, перпендикулярной прямой O’O» и проходящей через точку O .
Сечение призмы и вписанной в нее сферы плоскостью, перпендикулярной прямой O’O» и проходящей через точку O , представляет собой многоугольник, равный основаниям призмы, со вписанной в него окружностью радиуса R (рис. 3).
Следствие. В любой куб куб можно вписать сферу.
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Отношение объемов шара и куба, описанного около сферы, ограничивающей этот шар
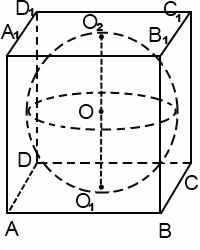
Задача 1. Найти отношение объемов шара и куба, описанного около сферы, ограничивающей этот шар.
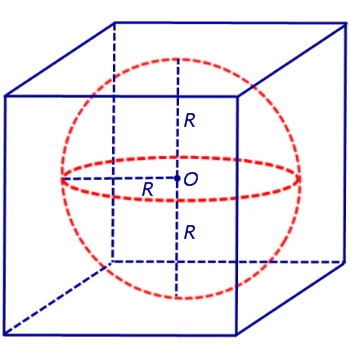
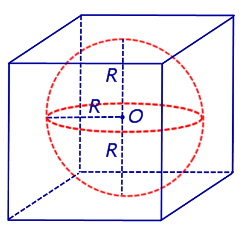
Решение. Если сфера радиуса R вписана в куб, то ребро куба равно 2R (рис. 4).
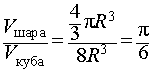 | (1) |
Ответ.
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Свойства правильной призмы, описанной около сферы.
Отношение объемов шара и правильной n — угольной призмы,
описанной около сферы, ограничивающей этот шар
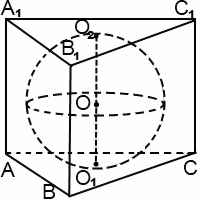
Задача 2. В правильную n — угольную призму с ребром основания a вписана сфера. Найти:
- Высоту призмы;
- Отношение объемов шара, ограниченного вписанной в правильную n — угольную призму сферой, и призмы.
Следствие 1. Отношение объема шара к объему правильной треугольной призмы, правильной треугольной призмы, описанной около сферы, ограничивающей этот шар, равно
Следствие 2. Отношение объема шара к объему правильной четырехугольной призмы, правильной четырехугольной призмы, описанной около сферы, ограничивающей этот шар, равно
Замечание. Как мы видим, при n = 4 формула для отношения объемов в ответе (пункт 2) совпадает с формулой (1).
Следствие 3. Отношение объема шара к объему правильной шестиугольной призмы, описанной около сферы, ограничивающей этот шар, равно
Видео:ВПИСАННАЯ И ОПИСАННАЯ ПРИЗМЫ // СТЕРЕОМЕТРИЯСкачать

Узнать ещё
Знание — сила. Познавательная информация
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Шар, вписанный в призму
Шар вписанный в призму, касается каждой ее грани. Диаметр вписанного шара равен высоте призмы, а также равен диаметру окружности, вписанной в основание призмы.
Центр шара лежит на середине высоты призмы, проведенной через центр вписанной в основание окружности. Если в основание призмы нельзя вписать окружность либо высота призмы не равна диаметру вписанной в основание окружности, то в такую призму шар вписать нельзя.
Если призма правильная, центр вписанного в нее шара является точкой пересечения бисекторных плоскостей призмы.
При решении задач на шар,вписанный в призму, можно рассмотреть сечение комбинации тел плоскостью, параллельной основаниям. Она представляет собой многоугольник, равный многоугольнику основания, с вписанной в него окружностью, радиус которой равен радиусу шара. Далее используем формулы, связывающие радиус вписанной окружности со сторонами основания, а также то, что центр вписанной в многоугольник окружности является точкой пересечения его биссектрис.
Выразим объем призмы через радиус вписанного шара — R. Объем призмы равен
Площадь основания ищем по формуле S=pr, где p — полупериметр основания, r — радиус вписанной в него окружности. Поскольку в нашем случае r=R и высота призмы H=2R, то
Но 2p=P — периметру основания. Окончательно имеем
Выразим площадь полной поверхности прямой призмы через радиус вписанного в нее шара. Площадь полной поверхности прямой призмы равна сумме площадей оснований и боковой поверхности:
Видео:Призма, вписанная в цилиндр.The prism inscribed in the cylinder.Скачать

Призма
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Призма
Призма – это многогранник, состоящий из двух равных многоугольников, расположенных в параллельных плоскостях, и $n$-го количества параллелограммов.
Многоугольники $ABCD$ и $A_1B_1C_1D_1$ – называются основаниями призмы.
Параллелограммы $АА_1В_1В, ВВ_1С_1С$ и т.д.- боковыми гранями.
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.
Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае – наклонной. Высота прямой призмы равна ее боковому ребру.
Формулы вычисления объема и площади поверхности призмы:
Чтобы были понятны формулы, введем обозначения:
$P_$ — периметр основания;
$S_$ — площадь основания;
$S_$ — площадь боковой поверхности;
$S_$ — площадь полной поверхности;
$h$ — высота призмы.
В основании призмы могут лежать различные многоугольники, рассмотрим площади некоторых из них.
В основании лежит треугольник.
- $S=/$, где $h_a$ — высота, проведенная к стороне $а$
- $S=/$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
- Формула Герона $S=√
$, где $р$ — это полупериметр $p=/$
- $S=p·r$, где $r$ — радиус вписанной окружности
- $S=/$, где $R$ — радиус описанной окружности
- Для прямоугольного треугольника $S=/$, где $а$ и $b$ — катеты прямоугольного треугольника.
В основании лежит четырехугольник
1. Прямоугольник
$S=a·b$, где $а$ и $b$ — смежные стороны.
2. Ромб
$S=/$, где $d_1$ и $d_2$ — диагонали ромба
$S=a^2·sinα$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.
3. Трапеция
$S=/$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.
Прямая призма называется правильной, если ее основания – правильные многоугольники.
Рассмотрим площади правильных многоугольников:
1. Для равностороннего треугольника $S=/$, где $а$ — длина стороны.
$S=a^2$, где $а$ — сторона квадрата.
3. Правильный шестиугольник
Шестиугольник разделим на шесть правильных треугольников и найдем площадь как:
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными $10$ и $24$, а её боковое ребро равно $20$.
Построим прямую призму, в основании которой лежит ромб.
Распишем формулу площади полной поверхности:
В прямой призме высота равна боковому ребру, следовательно, $h=С_1С=20$
Чтобы найти периметр основания, надо узнать сторону ромба. Рассмотрим один из прямоугольных треугольников, получившихся, при пересечении диагоналей и воспользуемся теоремой Пифагора.
Диагонали точкой пересечения делятся пополам, поэтому катеты прямоугольного треугольника равны $5$ и $12$.
Теперь найдем площадь основания: площадь ромба равна половине произведения его диагоналей.
Далее подставим все найденные величины в формулу полной поверхности и вычислим ее:
Цилиндр — это та же призма, в основании которой лежит круг.
Подобные призмы: при увеличении всех линейных размеров призмы в $k$ раз, её объём увеличится в $k^3$ раз.
Средняя линия треугольника параллельна основанию и равна его половине.
$MN$ — средняя линия, так как соединяет середины соседних сторон.
Подобие треугольников
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника больше сходственных сторон другого треугольника в некоторое число раз.
Число $k$ — коэффициент подобия (показывает во сколько раз стороны одного треугольника больше сторон другого треугольника.)
- Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$.
- Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Прямоугольный треугольник и его свойства:
В прямоугольном треугольнике катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
- Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
- Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$
Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом (sin) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом (tg) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
- Котангенсом (ctg) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
- В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
- Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
- Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | $/$ | $/$ | $/$ |
| $cosα$ | $/$ | $/$ | $/$ |
| $tgα$ | $/$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | $/$ |
Теорема синусов
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
Теорема косинусов
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
📽️ Видео
Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Геометрия 8 класс (Урок№32 - Вписанная окружность.)Скачать

8 класс, 38 урок, Вписанная окружностьСкачать

Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

Призма, описанная около шара, или шар, вписанный в призму.Скачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

GeoGebra: цилиндр, вписанный в правильную призмуСкачать

Окружность вписана в равносторонний треугольник, найти радиусСкачать

Призма, вписанная в шар. Prism, inscribed in a ball.Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

8 класс Геометрия. Окружность вписанная в четырехугольник и описанная около четырехугольника Урок #4Скачать

Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Как построить шестиугольник вписанный в окружностьСкачать