
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Уравнение дуги окружности в векторной форме записи
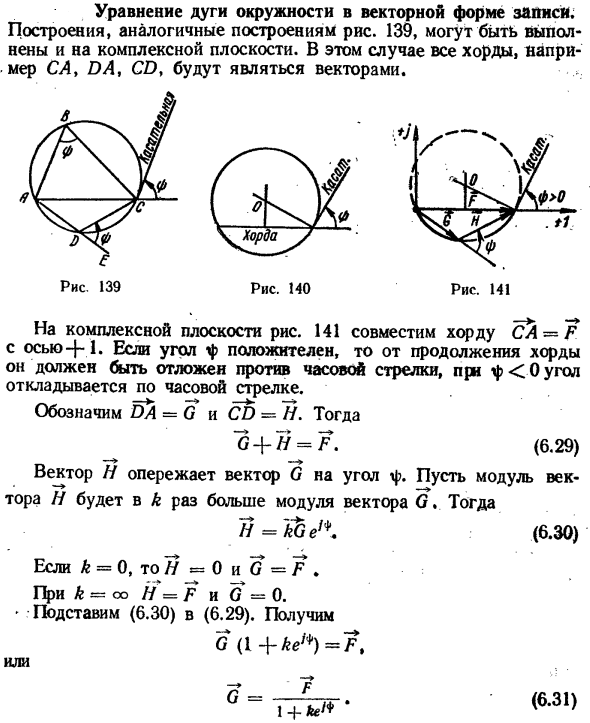
Уравнение дуги в векторной нотации. Структура 139, аналогичная структуре рисунка, может быть выполнена на комплексе plane. In в этом случае весь код, такой как SL, PL, SP и т. д. будут векторы.
- На комплексной плоскости рисунка 141 хорда C A-F совместима с осью 4 * h, если φ Людмила Фирмаль
Указывает DA = G и CD = N. — Г + Ч = Ф(6.29) Вектор H более продвинут на угол f, чем вектор G. модуль вектора H умножается на K модуля вектора G. H = кг A(6.30) Если Λ= 0, то 7? = 0 и G =? 。 если k-co H = F и G-0. Заменить ’(6.29) на ’ (6.30).Возьми Г(1 -] — ке^) = Ф Или X 7 (6.31)
Уравнение (6.31) называется уравнением дуги окружности в векторной системе счисления. * ?.-•••
- Если коэффициент£изменяется от 0 до Людмила Фирмаль
Важно отметить, что рабочая часть окружности или рабочая дуга-это та часть окружности, которая находится по другую сторону касательной к хорде F(рабочая дуга на рисунке 141 нарисована сплошной линией, а не сплошной линией).




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Окружность. 7 класс.Скачать

Уравнение дуги окружности в векторной форме записи
Построения, аналогичные построениям на рис. 4.18, а, могут быть выполнены и на комплексной плоскости. В этом случае все хорды, например СА, DA, DC, являются векторами.
На комплексной плоскости (рис. 4.18, в) совместим хорду CA = F с осью +1. Если угол |/ > 0, то от продолжения хорды его откладывают против часовой стрелки; если р 90°.
Видео:Математика это не ИсламСкачать

Круговые диаграммы
Из параграфа 3.4 известно, что синусоидально изменяющиеся функции времени (токи, напряжения) могут быть изображены векторами на комплексной плоскости. Если процесс в электрической цепи описывается уравнением, по форме тождественным уравнению (4.69), то геометрическим местом концов вектора тока (напряжения), выполняющего в уравнении электрической цепи те же функции, что и вектор G в уравнении (4.69), является окружность.
Под круговой диаграммой тока или напряжения понимают дугу окружности, являющуюся геометрическим местом концов вектора тока (напряжения) при изменении по модулю какого-либо сопротивления электрической цепи и сохранении неизменными остальных сопротивлений, частоты и ЭДС источников энергии.
С помощью круговых диаграмм производят графический анализ работы электрических цепей.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Циркулярные кривые 2-го порядка
Как известно, кривыми Безье нельзя построить дугу окружности или эллипса. В этой статье рассматриваются кривые, лишённые такого недостатка.
Видео:Как быстро распределить объекты по окружности в Corel DrawСкачать

Кривые Безье
Логика построения кривых Безье хорошо понятна из следующей анимации:
Чтобы получить формулу непосредственно из графического представления, достаточно определить вспомогательную функцию для линейной интерполяции между двумя точками, в которая при изменении параметра t от 0 до 1 возвращает промежуточные значения от a до b:
С её помощью можно последовательно найти необходимые точки — сначала найти
а затем уже через них найти
При желании, можно подставить функции друг в друга и сократить — хотя это особо и не упростит вычисления, зато позволит обобщить кривые на произвольное количество опорных точек (через полиномы Бернштейна). В нашем случае получим
Увеличение порядка кривых достигается тривиально — исходные точки задаются не константно, а как результат интерполяции между n+1 других контрольных точек:
Видео:начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Циркулярные кривые
Дуга окружности
Чтобы похожим образом построить дугу окружности, необходимо определить соответствующую логику построения — по аналогии с черчением окружности циркулем.
Изначально нам неизвестен центр окружности d — он находится через пересечение перпендикуляров к касательным в точках a и b (далее узловых); сами же касательные задаются с помощью точки c (далее направляющей). Для построения произвольной дуги окружности (меньшей 180°) достаточно, чтобы расстояния от направляющей точки до узловых были одинаковыми.
Дуга эллипса
Построить дугу эллипса уже посложнее — потребуется два вектора, вращающихся в разные стороны (подробнее здесь)
Используя озвученный выше способ нахождения точки d, мы уже не можем построить произвольную дугу эллипса — только лишь от 0° до 90° (в том числе и повёрнутую на некоторый угол).
Дуга гипотрохоиды
Задав условие, что в начале и конце черчения векторы должны лежать на одной прямой, мы получим дугу гипотрохоиды во всех остальных случаях. Это условие не случайно и (помимо однозначного определения кривой) гарантирует совпадение касательных в узловых точках. Как следствие, угловые пути, которые проходят оба вектора, станут разными, но в сумме по-прежнему будут давать 180°.
Как изменяется форма кривой в зависимости от положения направляющей точки, можно посмотреть на следующей анимации:
Видео:Как быстро распределить объекты по окружности в Adobe IllustratorСкачать

Алгоритм
Поскольку здесь мы имеем вращения на двумерной плоскости, математику построения этих кривых удобно описывать через комплексные числа.
1) находим точку пересечения нормалей касательных, проведённых от направляющей точки к узловым:
(здесь звёздочка означает комплексное сопряжение).
2) зная d, находим длины нормалей
и их сумму и разность
3) находим единичный вектор, от которого начинается построение
4) находим угловые пути, которые должны пройти каждый из векторов
При умножении векторов их длины умножаются, а углы — складываются. Здесь деление используется для противоположной задачи — найти разницу углов, т. е. угол между векторами.
Поскольку для функции аргумента длина вектора не играет роли, тот же результат можно получить и заменив деление умножением на комплексно сопряжённый вектор — такой вариант даже предпочтительнее, поскольку будет более численно устойчив на очень малых значениях из-за отсутствия деления; здесь же выбор в пользу деления сделан исключительно ради наглядности.
Здесь имеется ещё один крайне важный момент. Если бы мы сначала нашли углы для каждого вектора по отдельности, а потом бы считали разницу как
— результат не всегда был бы корректным из-за многозначности функции аргумента.
5) последовательно изменяя t от 0 до 1 с некоторым шагом, находим принадлежащую кривой точку по формуле
Видео:5 класс, 22 урок, Окружность и кругСкачать

Циркулярные сплайны
Так же, как и кривые Безье, эти кривые можно совмещать для кусочно-непрерывного построения сплайнов. Для обеспечения гладкости в узловых точках (стыковки) необходимо, чтобы узловая точка находилась на одной линии с двумя соседними направляющими точками. Для этого можно задавать узловые точки не явным образом, а через интерполяцию направляющих точек. Их также можно не задавать вообще, вычисляя полностью автоматически — например, как среднее между направляющих точек:
Справа для сравнения использован тот же подход с кривыми Безье 2-го порядка.
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Замечания и нюансы
В отличие от кривых Безье, здесь кривая не всегда лежит внутри фигуры из линий, соединяющих контрольные точки, например
Кроме того, существует вырожденный случай, который необходимо обрабатывать отдельно — когда направляющая точка лежит на одной прямой с узловыми точками. При этом кривая вырождается в прямую, а при попытке вычислить точку d возникает деление на ноль.
У этих кривых также имеется ограничения на кривизну линии, поскольку в соответствии с алгоритмом выбирается наименьший путь следования и кривая не может обогнуть больше, чем 180°. Это приводит к тому, что при кусочно-непрерывной интерполяции могут возникать острые углы при определённом положении направляющих точек (справа — те же точки для Безье):
Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Заключение
Дальнейшим развитием рассмотренного метода построения кривых является увеличение количества векторов, участвующих в построении кривой и, соответственно, увеличение количества направляющих точек. Однако, в отличие от кривых Безье, повышение порядка здесь не является очевидным и требует отдельного вдумчивого размышления. Также возможны различные методы комбинации их с кривыми Безье — в частности, интерполяции центра окружности рисующих векторов.
Рассмотренный метод построения кривых также не является единственным, частным случаем которого являются дуги окружности и эллипса — как минимум, эллипс можно построить через пересечение прямых в параллелограмме (правда, в этом варианте автор потерпел неудачу). Возможно, что существуют и другие решения, в том числе и варианты описанного в статье — пишите в комментариях, если вам что-то известно на эту тему.
Исходный код статьи можно скачать на GitHub.
📺 Видео
Физика - движение по окружностиСкачать

ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Центростремительное ускорение. 9 класс.Скачать

Archicad Штриховка в форме окружностиСкачать

10 класс, 11 урок, Числовая окружностьСкачать

Урок 89. Движение по окружности (ч.1)Скачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

ЕГЭ ПО МАТЕМАТИКЕ | ДВИЖЕНИЕ ПО ОКРУЖНОСТИ | +1 БАЛЛ ЗА 5 МИНУТ |Скачать