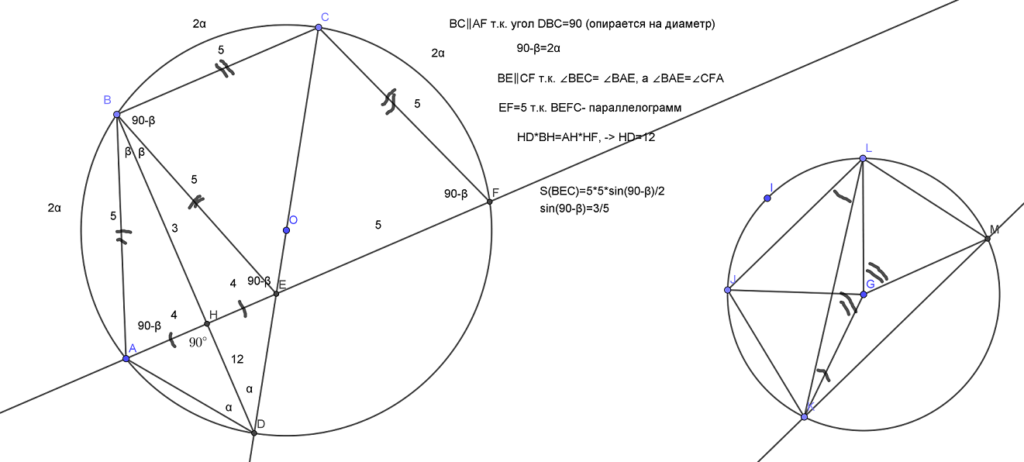
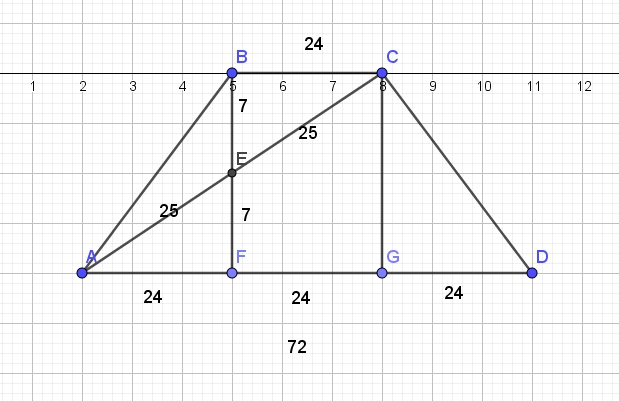
Окружность с центром О1 касается оснований ВС и AD и боковой стороны АВ трапеции ABCD. Окружность с центром O2 касается сторон ВС, CD и AD. Известно, что АВ = 10, ВС = 9, CD = 30, AD = 39.
а) Докажите, что прямая О1О2 параллельна основаниям трапеции АВСD.
а) Точка О1 равноудалена от прямых AD и ВС. Значит, точка О1 лежит на средней линии трапеции АВСD. Аналогично точка О2 лежит на средней линии трапеции АВСD, а значит, прямая О1О2 параллельна основаниям трапеции АВСD.
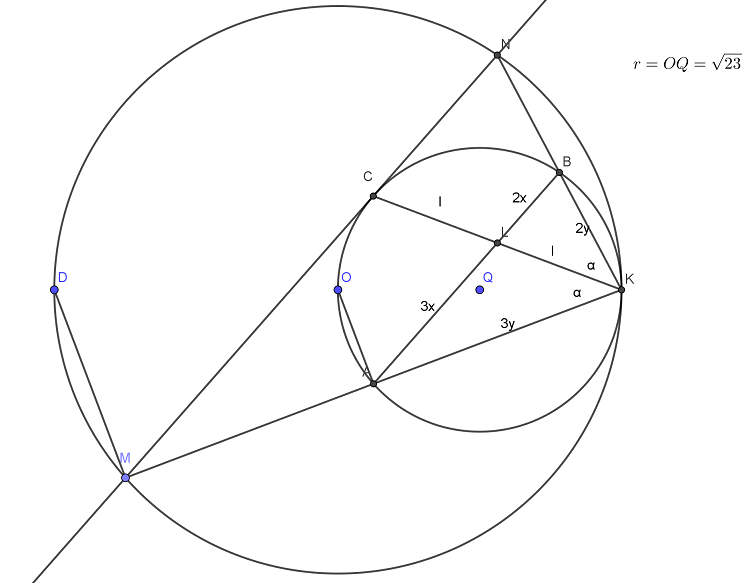
б) Пусть К — середина стороны АВ, а L — середина стороны CD. Точка О1 равноудалена от прямых АВ, ВС и AD, поэтому лучи АО1 и ВО1 являются биссектрисами углов DAB и ABC соответственно. Значит,
то есть Следовательно, КО1 — медиана, проведенная к гипотенузе АВ прямоугольного треугольника АО1В.
Аналогично треугольник СО2D прямоугольный, а LO2 — медиана, проведенная к его гипотенузе CD. Точки К, О1, О2 и L лежат на средней линии трапеции АВСD. Значит,
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Содержание
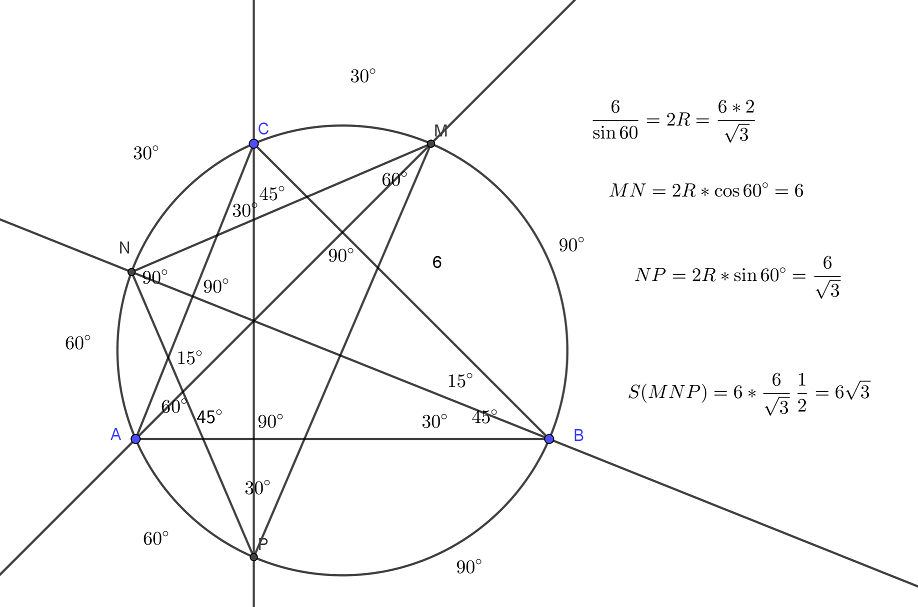
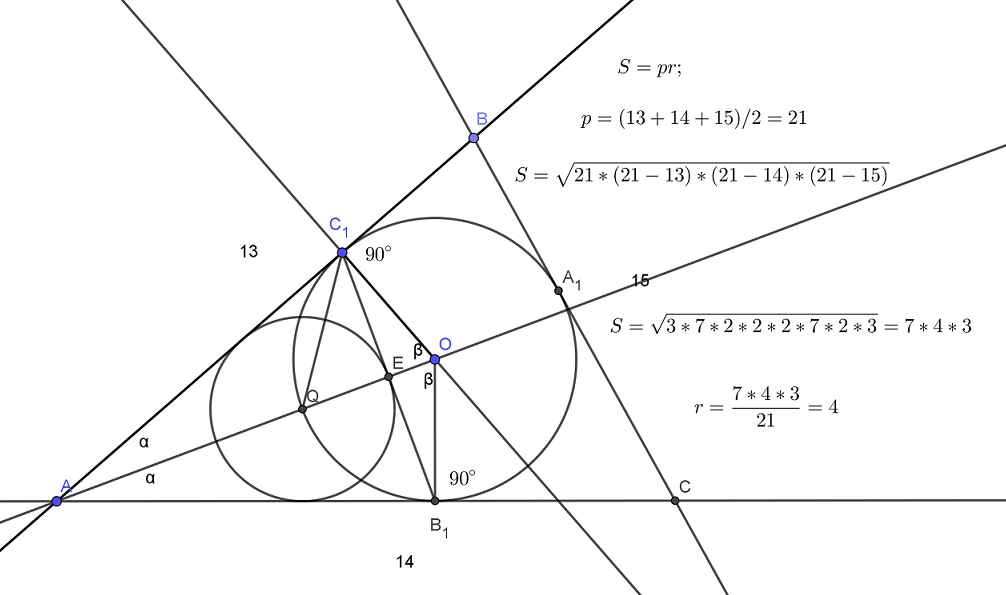
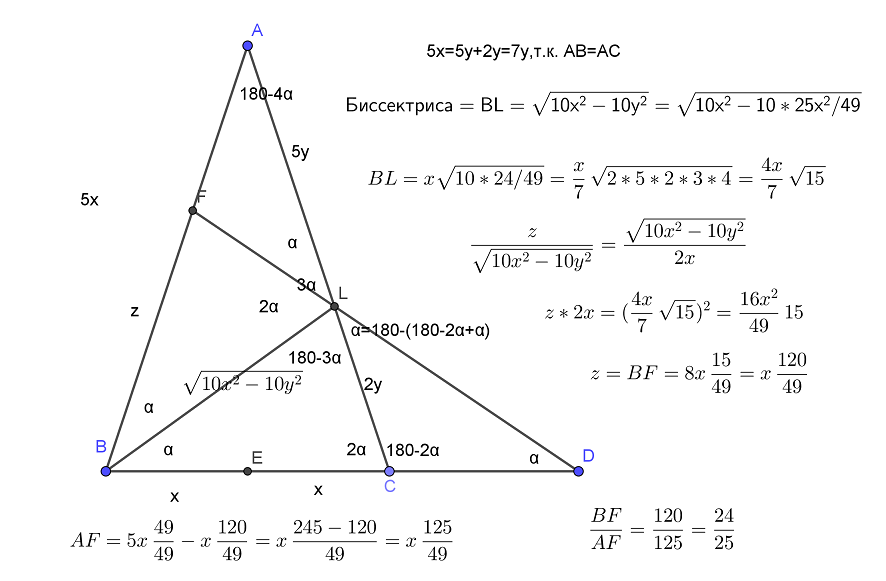
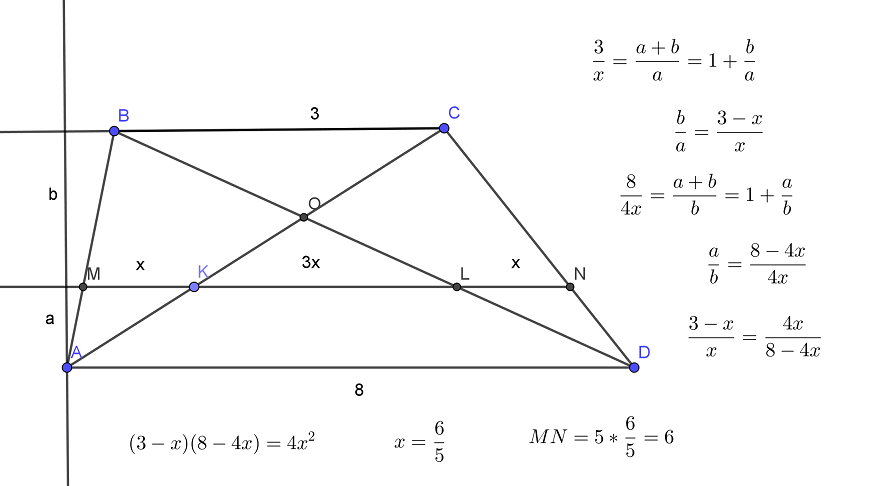
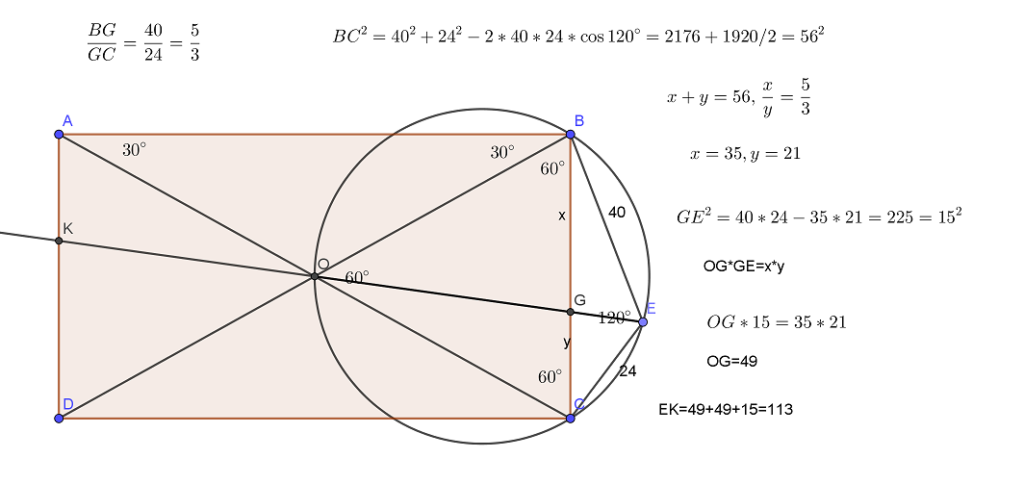
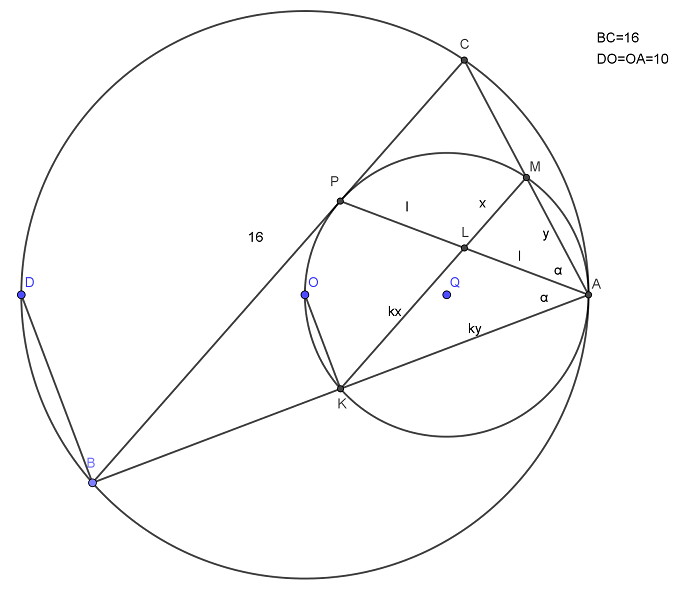
Видео:Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать  Рубрика: Задание 16 (планиметрия)Видео:🔴 В окружности с центром O отрезки AC и BD ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать  Решение задания 16, вариант 7, Ященко 36 вариантов, ЕГЭ-2019 (видео)Окружность с центром O1 касается оснований BC и AD, а также боковой стороны AB трапеции ABCD. Окружность с центром O2 касается сторон BC, CD и AD. Известно, что AB=9, BC=8, CD=4, AD=15. а) Докажите, что прямая 0102 параллельна основаниям трапеции Читать далее … Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать  Реальный ЕГЭ 2го июня 2017, задание 16Дана трапеция ABCD с диагоналями равными 8 и 15. Сумма оснований трапеции равна 17. а) Докажите, что диагонали перпендикулярны. б) Найдите высоту трапеции Сделаем дополнительное построение — проведем . Тогда , а т.к. BECD — параллелограмм. В треугольнике ACE стороны Читать далее … Видео:Геометрия Две окружности радиуса R с центрами O1 и O2 касаются друг друга. Их пересекает прямаяСкачать  Реальный ЕГЭ 29 мая 2019, задание 16В остроугольном треугольнике ABC все стороны различны. Прямая, содержащая высоту BH треугольника ABC, вторично пересекает описанную около этого треугольника окружность в точке K. Отрезок BN — диаметр этой окружности. a) Докажите, что AN=CK b) Найдите NK, если радиус описанной около Читать далее … Видео:ЕГЭ Задание 16 Две касающиеся окружностиСкачать  Решение задания 16, вариант 36, Ященко 36 вариантов, ЕГЭ-2018Дан прямоугольный треугольник ABC с прямым углом C. На катете AC взята точка М. Окружность с центром О и диаметром СМ касается гипотенузы в точке N. а) Докажите, что MN и ВО параллельны. б) Найдите площадь четырёхугольника BOMN,если СN=4 и Читать далее … Видео:ЕГЭ задание 16Скачать  Решение задания 16, вариант 35, Ященко 36 вариантов, ЕГЭ-2018Отрезок, соединяющий середины M и N оснований BC и AD соответственно трапеции ABCD, разбивает её на две трапеции, в каждую из которых можно вписать окружность. а) Докажите, что трапеция ABCD равнобедренная. б) Известно, что радиус этих окружностей равен 4, а Читать далее … Видео:№146. Отрезки АВ и CD — диаметры окружности с центром О. Найдите периметр треугольника AOD, еслиСкачать  Решение задания 16, вариант 34, Ященко 36 вариантов, ЕГЭ-2018Основание и боковая сторона равнобедренного треугольника равны 10 и 12 соответственно. а) Докажите, что средняя линия треугольника, параллельная основанию, пересекает окружность, вписанную в треугольник. б) Найдите длину отрезка этой средней линии, заключенного внутри окружности. Решение полностью аналогично варианту 15, посмотрите Читать далее … Видео:Ященко 2023, 12 вариантов. Вариант 3, задание 16.Скачать  Решение задания 16, вариант 33, Ященко 36 вариантов, ЕГЭ-2018Отрезок, соединяющий середины M и N оснований BC и AD соответственно трапеции ABCD, разбивает её на две трапеции, в каждую из которых можно вписать окружность. а) Докажите, что трапеция ABCD равнобедренная. б) Известно, что радиус этих окружностей равен 2, а Читать далее … Видео:Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать  Решение задания 16, вариант 32, Ященко 36 вариантов, ЕГЭ-2018Вневписанная окружность равнобедренного треугольника касается его боковой стороны. а) Докажите, что радиус этой окружности равен высоте треугольника, опущенной на основание. б) Известно, что радиус этой окружности в 6 раз больше радиуса вписанной окружности треугольника. В каком отношении точка касания вписанной Читать далее … Видео:№13 ЕГЭ 2023 по математике. Как начать понимать стереометрию?Скачать  Решение задания 16, вариант 31, Ященко 36 вариантов, ЕГЭ-2018Четырёхугольник ABCD вписан в окружность, причём сторона CD — диаметр этой окружности. Продолжение перпендикуляра AH к диагонали BD пересекает сторону CD в точке E, а окружность — в точке F, причём H — середина AE. а) Докажите, что четырёхугольник BCFE Читать далее … Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать  Решение задания 16, вариант 30, Ященко 36 вариантов, ЕГЭ-2018Четырёхугольник ABCD вписан в окружность, причём сторона CD — диаметр этой окружности. Продолжение перпендикуляра AH к диагонали BD пересекает сторону CD в точке E, а окружность — в точке F, причём H — середина AE. а) Докажите, что четырёхугольник BCFE Читать далее … Видео:№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать  Решение задания 16, вариант 29, Ященко 36 вариантов, ЕГЭ-2018Четырёхугольник ABCD вписан в окружность, причём сторона CD — диаметр этой окружности. Продолжение перпендикуляра AH к диагонали BD пересекает сторону CD в точке E, а окружность — в точке F, причём H — середина AE. а) Докажите, что четырёхугольник BCFE Читать далее … Видео:🔴 В угол C, равный 165°, вписана окружность с ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать  Решение задания 16, вариант 28, Ященко 36 вариантов, ЕГЭ-2018Четырёхугольник ABCD вписан в окружность, причём сторона CD — диаметр этой окружности. Продолжение перпендикуляра AH к диагонали BD пересекает сторону CD в точке E, а окружность — в точке F, причём H — середина AE. а) Докажите, что четырёхугольник BCFE Читать далее … Видео:16 задание с досрока ЕГЭ 2023. 2 задачи . Реально сложноСкачать  Решение задания 16, вариант 27, Ященко 36 вариантов, ЕГЭ-2018Четырёхугольник ABCD вписан в окружность, причём сторона CD — диаметр этой окружности. Продолжение перпендикуляра AH к диагонали BD пересекает сторону CD в точке E, а окружность — в точке F, причём H — середина AE. а) Докажите, что четырёхугольник BCFE Читать далее … Видео:Планиметрия с окружностями | Задачи из ЕГЭ прошлых лет | №17 ЕГЭ по математикеСкачать  Решение задания 16, вариант 26, Ященко 36 вариантов, ЕГЭ-2018Диагональ AC прямоугольника ABCD с центром O образует со стороной AB угол 30°. Точка E лежит вне прямоугольника, причём ∠BEC = 120°. а) Докажите, что ∠CBE = ∠COE. б) Прямая OE пересекает сторону AD прямоугольника в точке K. Найдите EK, Читать далее … Видео:Разбор 3 варианта из сборника Ященко. Зонты | Математика ОГЭ 2023 | УмскулСкачать  Решение задания 16, вариант 25, Ященко 36 вариантов, ЕГЭ-2018Основание и боковая сторона равнобедренного треугольника равны 26 и 31 соответственно. а) Докажите, что средняя линия треугольника, параллельная основанию, пересекает окружность, вписанную в треугольник. б) Найдите длину отрезка этой средней линии, заключенного внутри окружности. Решение аналогично варианту 15, посмотрите решение Читать далее … Видео:№1035. В окружности проведены хорды АВ и CD, пересекающиеся в точке Е. Найдите острыйСкачать  Решение задания 16, вариант 24, Ященко 36 вариантов, ЕГЭ-2018В треугольнике ABC известно, что ∠BAC=60°, ∠ABC=45°. Продолжения высот треугольника ABC пересекают описанную около него окружность в точках M,N,P. а) Докажите, что треугольник MNP — прямоугольный. б) Найдите площадь треугольника MNP, если известно, что BC = 10. Решается в точности Читать далее … Видео:№1,17 | Все теория по планиметрии за 4 часа | Решаем все прототипы №1 из ФИПИСкачать  Решение задания 16, вариант 23, Ященко 36 вариантов, ЕГЭ-2018В треугольнике ABC известно, что ∠BAC=60°, ∠ABC=45°. Продолжения высот треугольника ABC пересекают описанную около него окружность в точках M,N,P. а) Докажите, что треугольник MNP — прямоугольный. б) Найдите площадь треугольника MNP, если известно, что BC = 6. Решение смотри на Читать далее … Видео:[7] Окружности с нуля для ЕГЭ по математике. Внешнее касание окружностей. Конструкция из демоверсии.Скачать ![[7] Окружности с нуля для ЕГЭ по математике. Внешнее касание окружностей. Конструкция из демоверсии.](https://i.ytimg.com/vi/Ddj3m-1b_G4/0.jpg) Решение задания 16, вариант 22, Ященко 36 вариантов, ЕГЭ-2018Основание и боковая сторона равнобедренного треугольника равны 34 и 49 соответственно. а) Докажите, что средняя линия треугольника, параллельная основанию, пересекает окружность, вписанную в треугольник. б) Найдите длину отрезка этой средней линии, заключенного внутри окружности. Решается в точности как вариант 15, Читать далее … Видео:ОГЭ Задание 24 Площадь треугольника, трапецииСкачать  Решение задания 16, вариант 21, Ященко 36 вариантов, ЕГЭ-2018Окружность с центром O, вписанная в треугольник ABC, касается его сторон АВ, АС и ВС в точках , и соответственно. Биссектриса угла А пересекает эту окружность в точке Q, лежащей внутри треугольника . а) Докажите, что – биссектриса угла . Читать далее … Решение задания 16, вариант 20, Ященко 36 вариантов, ЕГЭ-2018Окружность с центром O, вписанная в треугольник ABC, касается его сторон АВ, АС и ВС в точках , и соответственно. Биссектриса угла А пересекает эту окружность в точке Q, лежащей внутри треугольника . а) Докажите, что – биссектриса угла . Читать далее … Решение задания 16, вариант 19, Ященко 36 вариантов, ЕГЭ-2018Окружность с центром O, вписанная в треугольник ABC, касается его сторон АВ, АС и ВС в точках , и соответственно. Биссектриса угла А пересекает эту окружность в точке Q, лежащей внутри треугольника . а) Докажите, что – биссектриса угла . Читать далее … Решение задания 16, вариант 18, Ященко 36 вариантов, ЕГЭ-2018Окружность с центром O, вписанная в треугольник ABC, касается его сторон АВ, АС и ВС в точках , и соответственно. Биссектриса угла А пересекает эту окружность в точке Q, лежащей внутри треугольника . а) Докажите, что – биссектриса угла . Читать далее … Решение задания 16, вариант 17, Ященко 36 вариантов, ЕГЭ-2018Окружность с центром O, вписанная в треугольник ABC, касается его сторон АВ, АС и ВС в точках , и соответственно. Биссектриса угла А пересекает эту окружность в точке Q, лежащей внутри треугольника . а) Докажите, что – биссектриса угла . Читать далее … Решение задания 16, вариант 16, Ященко 36 вариантов, ЕГЭ-2018На отрезке BD взята точка С. Биссектриса BL равнобедренного треугольника ABC с основанием BC является боковой стороной равнобедренного треугольника BLD с основанием BD. а) Докажите, что треугольник DCL равнобедренный. б) Известно, что . В каком отношении прямая DL делит сторону Читать далее … Решение задания 16, вариант 15, Ященко 36 вариантов, ЕГЭ-2018Основание и боковая сторона равнобедренного треугольника равны 26 и 38 соответственно. а) Докажите, что средняя линия треугольника, параллельная основанию, пересекает окружность, вписанную в треугольник. б) Найдите длину отрезка этой средней линии, заключённого внутри окружности. Решение задания 16, вариант 14, Ященко 36 вариантов, ЕГЭ-2018Прямая, параллельная основаниям BC и AD трапеции ABCD, пересекает боковые стороны AB и CD в точках M и N соответственно. Диагонали AC и BD пересекаются в точке O. Прямая MN пересекает стороны OA и OD треугольника AOD в точках K Читать далее … Решение задания 16, вариант 13, Ященко 36 вариантов, ЕГЭ-2018Вневписанная окружность равнобедренного треугольника касается его боковой стороны а) Докажите, что радиус этой окружности равен высоте треугольника, опущенной на основание. б) Известно, что радиус этой окружности в 4 раза больше радиуса вписанной окружности треугольника. В каком отношении точка касания вписанной Читать далее … Решение задания 16, вариант 12, Ященко 36 вариантов, ЕГЭ-2018Диагональ AC прямоугольника ABCD с центром O образует со стороной AB угол 30°. Точка E лежит вне прямоугольника, причём ∠BEC = 120°. а) Докажите, что ∠CBE = ∠COE. б) Прямая OE пересекает сторону AD прямоугольника в точке K. Найдите EK, Читать далее … Решение задания 16, вариант 11, Ященко 36 вариантов, ЕГЭ-2018Две окружности касаются внутренним образом в точке A, причем меньшая проходит через центр большей. Хорда BC большей окружности касается меньшей в точке P. Хорды AB и AC пересекают меньшую окружность в точках K и M соответственно. a) Докажите, что прямые Читать далее … Решение задания 16, вариант 10, Ященко 36 вариантов, ЕГЭ-2018Две окружности касаются внутренним образом в точке K, причем меньшая проходит через центр большей. Хорда МN большей окружности касается меньшей в точке С.Хорды КМ и КN пересекают меньшую окружность в точках А и В соответственно,а отрезки КС и АВ пересекаются Читать далее … Решение задания 16, вариант 9, Ященко 36 вариантов, ЕГЭ-2018Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MB пересекает окружность с диаметром AB в точке Читать далее … Решение задания 16, вариант 8, Ященко 36 вариантов, ЕГЭ-2018Диагонали AC и BD четырехугольника ABCD, вписанного в окружность, пересекаются в т. P, причем BC=CD. a) Докажите, что AB:BC=AP:PD b) Найдите площадь треугольника COD, где O — центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD — диаметр Читать далее … Решение задания 16, вариант 7, Ященко 36 вариантов, ЕГЭ-2018В прямоугольной трапеции ABCD с прямым углом при вершине A расположены две окружности. Одна из них касается боковых сторон и большего основания AD, вторая — боковых сторон, меньшего основания BC и первой окружности. a) Прямая, проходящая через центры окружностей, пересекает Читать далее … Решение задания 16, вариант 6, Ященко 36 вариантов, ЕГЭ-2018В равнобедренной трапеции ABCD основание AD в три раза больше основания BC. a) Докажите, что высота BH трапеции разбивает основание AD на отрезки, один из которых в два раза больше другого b) Найдите расстояние от вершины B до середины диагонали Читать далее … Решение задания 16, вариант 5, Ященко 36 вариантов, ЕГЭ-2018В равнобедренной трапеции ABCD основание AD в три раза больше основания BC. a) Докажите, что высота BH трапеции разбивает основание AD на отрезки, один из которых в два раза больше другого b) Найдите расстояние от вершины B до середины диагонали Читать далее … Решение задания 16, вариант 4, Ященко 36 вариантов, ЕГЭ-2018В равнобедренной трапеции ABCD основание AD в три раза больше основания BC. a) Докажите, что высота BF трапеции разбивает основание AD на отрезки, один из которых в два раза больше другого b) Найдите расстояние от вершины B до середины диагонали Читать далее … Решение задания 16, вариант 3, Ященко 36 вариантов, ЕГЭ-2018В трапеции ABCD основание AD в два раза меньше основания BC. Внутри трапеции взяли точку M так, что углы BAM и CDM — прямые. a) Докажите, что BM=CM b) Найдите угол ABC, если угол BCD=85 градусов, а расстояние от точки Читать далее … Решение задания 16, вариант 2, Ященко 36 вариантов, ЕГЭ-2018В трапеции ABCD основание AD в два раза меньше основания BC. Внутри трапеции взяли точку M так, что углы BAM и CDM — прямые. a) Докажите, что BM=CM b) Найдите угол ABC, если угол BCD=57 градусов, а расстояние от точки Читать далее … Решение задания 16, вариант 1, Ященко 36 вариантов, ЕГЭ-2018В трапеции ABCD основание AD в два раза меньше основания BC. Внутри трапеции взяли точку M так, что углы BAM и CDM — прямые. a) Докажите, что BM=CM b) Найдите угол ABC, если угол BCD=64 градуса, а расстояние от точки Читать далее … Решение задания 16, вариант 10, Ященко 36 вариантов, ЕГЭ-2017Основные идеи: Точки A и B — середины KM и KN соответственно, т.к. внутренняя окружность проходит через центр внешней и т.к. по двум углам (). как средняя линия. Т.к. , то дуги BC и AC равны (т.к. , то , Читать далее … Присоединяйся в мои чаты, задавай в них мне вопросыРешения заданий по темам:Рубрики
Контакты:Whatsapp: Окружность с центром o1 касается оснований bc и adБАЗА ЗАДАНИЙ Задание № 16. Планиметрия с доказательством. 1. Прямая, проходящая через вершину B прямоугольника ABCD перпендикулярно диагонали AC, пересекает сторону AD в точке M, равноудалённой от вершин B и D. 2. К окружности, вписанной в квадрат ABCD, проведена касательная, пересекающая стороны AB и AD в точках M и N соответственно. 3. Диагонали AC и BD четырёхугольника ABCD, вписанного в окружность, пересекаются в точке P, причём BC=CD. 4. В треугольнике ABC точки A 1 , B 1 , C 1 — середины сторон BC, AC и A B соответственно, AH— высота, ∠BAC = 60°, ∠BCA = 45°. 5. Две окружности касаются внутренним образом в точке A, причём меньшая проходит через центр большей. Хорда BC большей окружности касается меньшей в точке P. Хорды AB и AC пересекают меньшую окружность в точках K и M соответственно. 6. Две окружности касаются внутренним образом в точке A, причём меньшая окружность проходит через центр O большей. Диаметр BC большей окружности вторично пересекает меньшую окружность в точке M, отличной от A. Лучи AO и AM вторично пересекают большую окружность в точках P и Q соответственно. Точка C лежит на дуге AQ большей окружности, не содержащей точку P. 7. Две окружности касаются внутренним образом в точке K, причём меньшая проходит через центр большей. Хорда MN большей окружности касается меньшей в точке C. Хорды KM и KN пересекают меньшую окружность в точках A и B соответственно, а отрезки KC и AB пересекаются в точке L. 8. Дан прямоугольный треугольник ABC с прямым углом C. На катете AC взята точка M. Окружность с центром O и диаметром CM касается гипотенузы в точке N. 9. Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MB пересекает окружность с диаметром AB в точке D. 10. Точка M лежит на стороне BC выпуклого четырёхугольника ABCD, причём B и C — вершины равнобедренных треугольников с основаниями AM и DM соответственно, а прямые AM и MD перпендикулярны. 11. В равнобедренном тупоугольном треугольнике ABC на продолжение боковой стороны BC опущена высота AH. Из точки H на сторону AB и основание AC опущены перпендикуляры HK и HM соответственно. 12. Точка O — центр окружности, описанной около остроугольного треугольника ABC, I — центр вписанной в него окружности, H — точка пересечения высот. Известно, что ∠BAC = ∠OBC+∠OCB. 13. Точки P, Q, W делят стороны выпуклого четырёхугольника ABCD в отношении AP:PB = CQ:QB = CW:WD = 3:4, радиус окружности, описанной около треугольника PQW, равен 10, PQ = 16, QW = 12, угол PWQ— острый. 14. Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках C 1 , B 1 соответственно. 15. Дана трапеция ABCD с основаниями AD и BC. Диагональ BD разбивает её на два равнобедренных треугольника с основаниями AD и CD. 16. В прямоугольном треугольнике АВС с прямым углом С точки М и N – середины катетов АС и ВС соответственно, СН – высота. 17. В треугольнике АВС угол АВС равен 60°. Окружность, вписанная в треугольник, касается стороны AC в точке M. 18. В треугольнике АВС проведены высоты АК и СМ. На них из точек М и К опущены перпендикуляры МЕ и КН соответственно. 19. Окружность, вписанная в треугольник KLM, касается сторон KL, LM, MK в точках A, B и C соответственно. б) Найдите отношение LB:BM, если известно, что KC:CM = 3:2 и ∠ MKL = 60. 20. Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром O, построенная на боковой стороне AB как на диаметре, касается боковой стороны CD и второй раз пересекает большее основание AD в точке H, точка Q — середина CD. 21. Квадрат ABCD вписан в окружность. Хорда CE пересекает его диагональ BD в точке K. 22. В прямоугольном треугольнике ABC точки M и N – середины гипотенузы AB и катета BC соответственно. Биссектриса ∠ BAC пересекает прямую MN в точке L 23. Окружность касается стороны AC остроугольного треугольника ABC и делит каждую из сторон AB и BC на три равные части. 24. На катетах AC и BC прямоугольного треугольника ABC как на диаметрах построены окружности, второй раз пересекающиеся в точке M. Точка Q лежит на меньшей дуге MB окружности с диаметром BC. Прямая CQ второй раз пересекает окружность с диаметром AC в точке P. 25. Окружность, построенная на медиане BM равнобедренного треугольника ABC как на диаметре, второй раз пересекает основание BC в точке K. 26. В прямоугольной трапеции ABCD с прямым углом при вершине A расположены две окружности. Одна из них касается боковых сторон и большего основания AD, вторая – боковых сторон, меньшего основания BC и первой окружности. 27. В трапецию ABCD с основаниями AD и BC вписана окружность с центром O. 28. Дана трапеция с диагоналями равными 8 и 15. Сумма оснований равна 17. |