Окружность с центром на гипотенузе прямоугольного треугольника

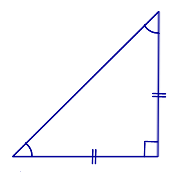Определение равнобедренного прямоугольного треугольника:

Равнобедренным прямоугольным треугольником называют такой прямоугольный треугольник, у которого равны катеты.

Свойство углов прямоугольного треугольника:

Острые углы равнобедренного прямоугольного треугольника равны 45° .

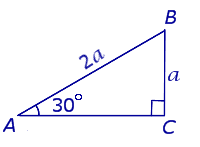Свойство прямоугольного треугольника с углом в 30° :

Катет прямоугольного треугольника, лежащий против угла в 30° , равен половине гипотенузы.

Признак прямоугольного треугольника с углом в 30° :

Если в прямоугольном треугольнике один из катетов равен половине гипотенузы, то этот катет лежит против угла в 30° .

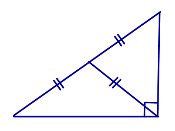Свойство медианы, проведенной к гипотенузе прямоугольного треугольника:

Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы.

Признак прямоугольного треугольника:

Если в треугольнике медиана равна половине стороны, к которой она проведена, то такой треугольник является прямоугольным.

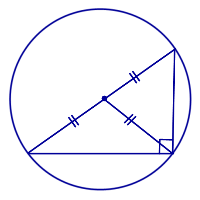Свойство окружности, описанной около прямоугольного треугольника:

Середина гипотенузы прямоугольного треугольника является центром описанной около него окружности.

Признак прямоугольного треугольника:

Если в треугольнике центр описанной окружности лежит на одной из сторон, то этот треугольник является прямоугольным треугольником, а центр описанной окружности совпадает с серединой гипотенузы.

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

Обратная теорема Пифагора:

Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то такой треугольник является прямоугольным

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Окружность, центр которой принадлежит гипотенуза прямоугольного треугольника, касается большего катета и проходит через вершину

Видео:Геометрия Окружность центр которой принадлежит гипотенузе прямоугольного треугольника касаетсяСкачать

Ваш ответ

Видео:№704. Окружность с центром О описана около прямоугольного треугольника, а) ДокажитеСкачать

Похожие вопросы

• Все категории
• экономические 43,279
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,949
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

Прямоугольный треугольник

Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).

Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.

Стороны, прилежащие к прямому углу, называются катетами .

Признаки равенства прямоугольных треугольников

Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и острому углу ).

Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).

Свойства прямоугольного треугольника

1. Сумма острых углов прямоугольного треугольника равна 90˚.

2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.

И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.

3. Теорема Пифагора:

, где – катеты, – гипотенуза. Видеодоказательство

4. Площадь прямоугольного треугольника с катетами :

5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты и гипотенузу следующим образом:

6. Центр описанной окружности – есть середина гипотенузы.

7. Радиус описанной окружности есть половина гипотенузы :

8. Медиана, проведенная к гипотенузе, равна ее половине

9. Радиус вписанной окружности выражается через катеты и гипотенузу следующим образом:

Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.

📺 Видео

Длина катета прямоугольного треугольника равна 8 см. Окружность с диаметром пересекает гипотенузуСкачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

2023 На окружности с центром в точке О отмечены точки А и Б так что угол аоб равен 45Скачать

Геометрия Центр окружности, вписанной в прямоугольный треугольник удален от концов гипотенузы на aСкачать

#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

Задача по геометрии на прямоугольный треугольник и теорему Пифагора из реального ОГЭ по математикеСкачать

ОГЭ. Задание 24. Геометрическая задача на вычисление.Скачать

ОГЭ. Задание 24. Геометрическая задача на вычислениеСкачать

Радиус окружности, описанной около прямоугольного треугольника, равен 4. Найдите гипотенузу.Скачать

Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Треугольник и окружность #shortsСкачать

№705. Около прямоугольного треугольника ABC с прямым углом С описана окружность. Найдите радиусСкачать

Как найти центр кругаСкачать

№1125. На сторонах прямоугольного треугольника как на диаметрах построены три полукруга.Скачать

ЕГЭ Задание 16 Вписанная окружность Теорема косинусовСкачать

Отрезки AC и BD – диаметры окружности с центром O ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать