Окружность пересекает стороны pq и qr треугольника pqr

Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AK = 18, а сторона AC в 1,2 раза больше стороны BC.

Это задание ещё не решено, приводим решение прототипа.

Окружность пересекает стороны A B и A C треугольника A B C в точках K и P соответственно и проходит через вершины B и C . Найдите длину отрезка K P , если A P = 16 , а сторона B C в 1,6 раза меньше стороны A B .

Видео:ОГЭ. Задание 24. Геометрическая задача на вычисление.Скачать

Решение №1128 Окружность пересекает стороны АВ и АС треугольника АВС в точках К и Р …

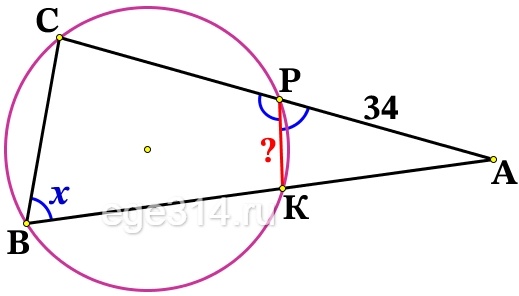
Окружность пересекает стороны АВ и АС треугольника АВС в точках К и Р соответственно и проходит через вершины В и С. Найдите длину отрезка КР, если АР = 34, а сторона ВС в 2 раза меньше стороны АВ.

Источник: ОГЭ 2021 Ященко (36 вар)

Четырёхугольник CBKP вписан в окружность, сумма противолежащих углов равна 180°. Пусть ∠В равен х , тогда противолежащий ∠СРК = 180° – х. Угол ∠АРК смежный к ∠СРК, тогда ∠АРК = 180 – (180 – х) = х. Значит ∠АРК = ∠В.
В ΔСАВ и ΔРАК: ∠АРК = ∠В, угол А общий, значит эти треугольники подобны по двум равным углам. Тогда и стороны подобны:

По условию АВ = 2·ВС , AP = 34 , тогда:

Ответ: 17.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 5 / 5. Количество оценок: 2

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время

В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.

Видео:ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

Обобщающий урок «Теоремы Менелая и Чевы»

Разделы: Математика

Цель:

• повторить и обобщить изученные теоремы;
• рассмотреть их применение при решении ряда задач;
• подготовка учащихся к вступительным экзаменам в ВУЗы;
• воспитывать эстетическое выполнение чертежей к задачам.

Оборудование: мультимедийный проектор. Приложение 1.

1. Организационный момент.

2. Проверка домашнего задания:

• доказательство теорем – 2 учащихся + 2 уч-ся – консультанты (проверяющие);
• решение домашних задач – 3 учащихся;
• работа с классом – устное решение задач:

Точка С₁ делит сторону АВ треугольника АВС в отношении 2 : 1. точка В₁ лежит на продолжении стороны АС за точку С, и АС = СВ₁. В каком отношении делит прямая В₁ С₁ сторону ВС? (на слайде 2).

Решение: По условиюИспользуя теорему Менелая, находим: .

В треугольнике АВС АD – медиана, точка О – середина медианы. Прямая ВО пересекает сторону АС в точке К.

В каком отношении точка К делит АС, считая от точки А? (на слайде 3).

Решение: Пусть ВD = DС = а, АО = ОD = m. Прямая ВК пересекает две стороны и продолжение третьей стороны треугольника АDС . По теореме Менелая .

В треугольнике АВС на стороне ВС взята точка N так, что NС = 3ВN; на продолжении стороны АС за точку А взята точка М так, что МА = АС. Прямая МN пересекает сторону АВ в точке F. Найдите отношение . (на слайде 4).

Решение: По условию задачи МА = АС, NС = 3 ВN. Пусть МА = АС = b, BN = k, NC = 3k. Прямая МN пересекает две стороны треугольника АВС и продолжение третьей. По теореме Менелая

.

На стороне PQ треугольника PQR взята точка N, а на стороне РR – точка L, причем NQ = LR. Точка пересечения отрезков QL и NR делит QR в отношении m : n, считая от точки Q. Найдите PN : PR. (на слайде 5).

Решение: По условию NQ = LR, . Пусть NA = LR = a, QF =km, LF = kn. Прямая NR пересекает две стороны треугольника PQL и продолжение третьей. По теореме Менелая

.

3. Отработка практических навыков.

1. Решение задач:

Докажите теорему: Медианы треугольника пересекаются в одной точке; точка пересечения делит каждую из них в отношении 2 : 1, считая от вершины. (рисунок 1 слайд 6).

Доказательство: Пусть АМ₁, ВМ₂, СМ₃ – медианы треугольника АВС. Чтобы доказать, что эти отрезки пересекаются в одной точке, достаточно показать, что Тогда по теореме Чевы (обратной) отрезки АМ₁, ВМ₂ и СМ₃ пересекаются в одной точке. Имеем:

Итак, доказано, что медианы треугольника пересекаются в одной точке.

Пусть О – точка пересечения медиан. Прямая М₃С пересекает две стороны треугольника АВМ₂ и продолжение третьей стороны этого треугольника. По теореме Менелая

или .

Рассматривая теорему Менелая для треугольников АМ₁С и АМ₂С, мы получаем, что

. Теорема доказана.

Докажите теорему: Биссектрисы треугольника пересекаются в одной точке. (рисунок 2 слайд 6).

Доказательство: Достаточно показать, что . Тогда по теореме Чевы (обратной) AL_1, BL_2, CL₃ пересекаются в одной точке. По свойству биссектрис треугольника:

. Перемножая почленно полученные равенства, получаем: . Итак, для биссектрис треугольника равенство Чевы выполняется, следовательно, они пересекаются в одной точке. Теорема доказана.

Докажите теорему: Высоты остроугольного треугольника пересекаются в одной точке. (рисунок 3 слайд 6).

Доказательство: Пусть АН₁, АН_2, АН₃ – высоты треугольника АВС со сторонами a, b, c. Из прямоугольных треугольников АВН₂ и ВСН₂ по теореме Пифагора выразим, соответственно, квадрат общего катета ВН₂, обозначив АН₂ = х, СН₂ = b – х.

(ВН₂) 2 = с 2 – х 2 и (ВН₂) 2 = а 2 – (b – х) 2 . приравнивая правые части полученных равенств, получаем с 2 – х 2 = а 2 – (b – х) 2 , откуда х = .

Тогда b –x = b — = .

Итак, АН₂ = , СН₂ = .

Аналогично рассуждая для прямоугольных треугольников АСН₂ и ВСН₃, ВАН₁ и САН₁, получим АН₃ = , ВН₃ = и ВН₁ = ,

СН₁ = .

Для доказательства теоремы достаточно показать, что . Тогда по теореме Чевы (обратной) отрезки АН₁, ВН₂ и СН₃ пересекаются в одной точке. Подставив в левую часть равенства выражения длин отрезков АН₃, ВН₃, ВН₁, СН₁, СН₂ и АН₂ через а, b, с, убеждаемся, что равенство Чевы для высот треугольника выполняется. Теорема доказана.

Задачи 5 – 7 самостоятельное решение 3 учащихся. (чертежи на экране).

2. остальные:

Докажите теорему: Если в треугольник вписана окружность, то отрезки, соединяющие вершины треугольника с точками касания противоположных сторон пересекаются в одной точке. (на рисунке 4 слайд 6).

Доказательство: Пусть А₁, В₁ и С₁ – точки касания вписанной окружности треугольника АВС. Для того, чтобы доказать, что отрезки АА₁, ВВ₁ и СС₁ пересекаются в одной точке, достаточно показать, что выполняется равенство Чевы:

. Используя свойство касательных, проведенных из одной точки, введем обозначения: ВС₁ = ВА₁ = х, СА₁ = СВ₁ = у, АВ₁ = АС₁ = z.

. Равенство Чевы выполняется, значит, указанные отрезки (биссектрисы треугольника) пересекаются в одной точке. Эту точку называют точкой Жергона. Теорема доказана.

3. Разбор задач 5, 6, 7.

Пусть АD – медиана треугольника АВС. На стороне АD взята точка К так, что АК : КD = 3 : 1. Прямая ВК разбивает треугольник АВС на два. Найдите отношение площадей этих треугольников. (на слайде 7 рисунок 1)

Решение: Пусть АD = DC = a, KD = m, тогда АК = 3m. Пусть Р – точка пересечения прямой ВК со стороной АС. Необходимо найти отношение . Так как треугольники АВР и РВС имеют равные высоты, проведенные из вершины В, то = . По теореме Менелая для треугольника ADC и секущей РВ имеем: . Итак, = .

В треугольнике АВС, описанном около окружности, АВ = 8, ВС = 5, АС = 4. А₁ и С₁ – точки касания, принадлежащие соответственно сторонам ВС и ВА. Р – точка пересечения отрезков АА₁ и СС₁. Точка Р лежит на биссектрисе ВВ₁. Найдите АР : РА₁.

(на слайде 7 рисунок 2)

Решение: Точка касания окружности со стороной АС не совпадает с В₁, так как треугольник АВС – разносторонний. Пусть С₁В = х, тогда, используя свойство касательных, проведенных к окружности из одной точки, введем обозначения (см рисунок) 8 – х + 5 – х = 4, х = .

Значит, С₁В = ВА₁ = , А₁С = 5 — = , АС₁ = 8 — = .

В треугольнике АВА₁ прямая С₁С пересекает две его стороны и продолжение третьей стороны. По теореме Менелая .

Стороны треугольника 5, 6 и 7. Найдите отношение отрезков, на которые биссектриса большего угла этого треугольника разделена центром окружности, вписанной в треугольник. (на слайде 7).

Решение: Пусть в треугольнике АВС АВ = 5, ВС = 7, АС = 6. Угол ВАС лежит против большей стороны в треугольнике АВС, значит, угол ВАС – больший угол треугольника. Центр вписанной окружности треугольника лежит на пересечении биссектрис. Пусть О – точка пересечения биссектрис. Необходимо найти АО : ОD. Так как АD – биссектриса треугольника АВС, то , то есть BD = 5k, DС = 6k. так как BF – биссектриса треугольника АВС, то , то есть AF = 5m, FC = 7m. Прямая BF пересекает две стороны и продолжение третьей стороны треугольника ADC. По теореме Менелая .

4. Самостоятельное решение задач 9, 10, 11. – 3 учащихся.

Задача 12 (для всех оставшихся учащихся класса):

Биссектрисы ВЕ и АD треугольника АВС пересекаются в точке Q. Найдите площадь треугольника АВС, если площадь треугольника BQD = 1, 2АС = 3 АВ, 3ВС = 4 АВ. (рисунок 4 на слайде 7).

Решение: Пусть АВ = а, тогда АС = , ВС = . АD — биссектриса треугольника АВС, тогда , то есть BD = 2p, DC = 3p. ВЕ – биссектриса треугольника АВС, тогда , АЕ = 3 k, ЕС = 4k. В треугольнике ВЕС прямая АD пересекает две его стороны и продолжение третьей стороны. По теореме Менелая , , , то есть EQ = 9m, QB = 14m. Треугольники QBD и EBC имеют общий угол, значит , S_ЕВС = .

Треугольники АВС и ВЕС имеют равные высоты, проведенные из вершины В, значит, , тогда S_ABC = _.

5. Разбор задач 9, 10, 11.

Решение задач – практикум:

А. На сторонах ВС, СА, АВ равнобедренного треугольника АВС с основанием АВ взяты точки А_1, В₁, С_1, так что прямые АА₁, ВВ₁, СС₁ – конкурентные.

Докажите, что

По теореме Чевы имеем: (1 ).

По теореме синусов:, откуда СА₁ = СА .,

, откуда А₁В = АВ . , ,

откуда АВ₁ = АВ . , , откуда В₁С = ВС . , так как СА = ВС по условию. Подставив полученные равенства в равенство (1 ) получим:

.

Что и требовалось доказать.

В. На стороне АС треугольника АВС взята такая точка М, что АМ = ?АС, а на продолжении стороны ВС – такая точка N, что BN = СВ. В каком отношении точка Р – точка пересечения отрезков АВ и MN делит каждый из этих отрезков?

По теореме Менелая для треугольника АВС и секущей MN имеем:

. По условию следовательно ,

так как 0,5 . (-2) . х = 1, — 2х = — 2, х = 1.

Для треугольника MNC и секущей АВ по теореме Менелая имеем: по условию

значит, — , откуда, .

8. Самостоятельное решение задач: 1 вариант:

1. На продолжениях сторон АВ, ВС, АС треугольника АВС взяты соответственно точки С₁, А₁, В₁ так, что АВ = ВС₁, ВС = СА₁, СА = АВ₁. Найдите отношение в котором прямая АВ₁ делит сторону А₁С₁ треугольника А₁В₁С₁. (3 балла).

2. На медиане СС₁ треугольника АВС взята точка М. Прямые АМ и ВМ пересекают стороны треугольника соответственно в точках А₁ и В₁. Докажите, что прямые АВ и А₁В₁ параллельны. (3 балла).

3. Пусть на продолжении сторон АВ, ВС и АС треугольника АВС взяты соответственно точки С₁, А₁ и В_1. Докажите, что точки А₁, В_1, С₁ лежат на одной прямой тогда и только тогда, когда выполняется равенство . (4 балла).

4. Используя теорему Чевы, докажите, что высоты треугольника или их продолжения пересекаются в одной точке. (4 балла).

5. Докажите, что прямые, проходящие через вершины треугольника и точки касания вневписанных окружностей, пересекаются в одной точке (точке Нагеля). (Окружность называется вневписанной в треугольник, если она касается одной стороны этого треугольника и продолжений двух других его сторон). (5 баллов).

6. Пусть на сторонах АВ, ВС и АС треугольника АВС взяты соответственно точки С₁, А₁ и В₁ так, что прямые АА₁, ВВ₁, СС₁ пересекаются в точке О. Докажите, что выполняется равенство . (5 баллов).

7. Пусть на ребрах АВ, ВС, СD и АD тетраэдра АВСD взяты соответственно точки А₁, В₁, С₁, D_1. Докажите, что точки А₁, В₁, С₁, D₁ лежат в одной плоскости тогда и только тогда, когда выполняется равенство (5 баллов).

1. Точки А₁ и В₁ делят стороны ВС и АС треугольника АВС в отношениях 2 : 1 и 1 : 2. Прямые АА₁ и ВВ₁ пересекаются в точке О. Площадь треугольника АВС равна 1. Найдите площадь треугольника ОВС. (3 балла).

2. Отрезок МN, соединяющий середины сторон АD и ВС четырехугольника АВСD делится диагоналями на три равные части. Докажите, что АВСD – трапеция, одно из оснований АВ или СD, которое в двое больше другого. (3 балла).

3. Пусть на стороне АВ и продолжении сторон ВС и АС треугольника АВС взяты соответственно точки С₁, А₁ и В₁. Докажите, что прямые АА₁, ВВ₁, СС₁ пересекаются в одной точке или параллельны тогда и только тогда, когда выполняется равенство . (4 балла).

4. Используя теорему Чевы, докажите, что высоты треугольника или их продолжения пересекаются в одной точке. (4 балла).

5. Докажите, что прямые, проходящие через вершины треугольника и точки касания вневписанных окружностей, пересекаются в одной точке (точке Нагеля). (Окружность называется вневписанной в треугольник, если она касается одной стороны этого треугольника и продолжений двух других его сторон). (5 баллов).

6. Пусть на сторонах АВ, ВС и АС треугольника АВС взяты соответственно точки С₁, А₁, В₁ так, что прямые АА₁, ВВ₁ и СС₁ пересекаются в точке О. Докажите, что выполняется равенство . (5 баллов).

7. Пусть на ребрах АВ, ВС, СD и АD тетраэдра АВСD взяты соответственно точки А₁, В₁, С₁, D_1. Докажите, что точки А₁, В₁, С₁, D₁ лежат в одной плоскости тогда и только тогда, когда выполняется равенство (5 баллов).

9. Домашнее задание: учебник § 3, № 855, № 861, № 859.

🎦 Видео

Математика ОГЭ Задание 26 Отношение площадейСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать

ОГЭ 23 КАК РЕШИТЬ ЗАДАЧУ НА ПОДОБНЫЕ ТРЕУГОЛЬНИКИСкачать

2038 центр окружности описанной около треугольника ABC лежит на стороне ABСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

2031 окружность центром в точке О описана около равнобедренного треугольника ABCСкачать

На окружности по разные стороны от диаметра AB ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Задача на окружности из ОГЭ-2023!! Разбор за 30 секСкачать

№971. Напишите уравнение окружности, проходящей через точки А (-3; 0) и B (0; 9), если известноСкачать

Все типы 15 задания ОГЭ 2022 математика | Геометрия на ОГЭСкачать

ЕГЭ Математика Задание 6#27935Скачать

Как правильно решить задание про четырёхугольник? / Разбор заданий на ОГЭ по геометрииСкачать

Задание 16 ОГЭ по математике. Окружность описана около квадратаСкачать

Треугольник и окружность #shortsСкачать

№166. Отрезки АВ и CD пересекаются в их общей середине О. Точки М и N — середины отрезков АС и BD.Скачать

Решение Варианта 267 ОГЭ Ларн № 1 - 25Скачать

Хорды AC и BD окружности пересекаются в точке P, BP=6, CP=8, DP=12. Найдите AP.Скачать