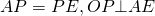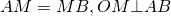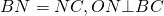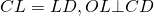Окружность описана около пятиугольника

Что такое описанная окружность? Какими свойствами она обладает?

Описанная около выпуклого многоугольника окружность — это окружность, которая проходит через все вершины многоугольника.

Многоугольник, около которого описана окружность, называется вписанным.

В выпуклый многоугольник можно вписать окружность, если все серединные перпендикуляры к его сторонам пересекаются в одной точке.

Центр вписанной в многоугольник окружности — точка пересечения серединных перпендикуляров к его сторонам.

Центр описанной окружности равноудалён от вершин многоугольника.

Расстояние от центра до любой вершины многоугольника равно радиусу описанной окружности.

Окружность с центром в точке O и радиусом R описана около пятиугольника ABCDE.

ABCDE — вписанный пятиугольник.

O — точка пересечения серединных перпендикуляров к сторонам ABCD, то есть

Точка O равноудалена от вершин пятиугольника.

Расстояние от точки O до любой вершины равно радиусу:

Около любого правильного многоугольника можно описать окружность. В любой правильный многоугольник также можно вписать окружность. Центр вписанной и описанной окружности лежат в центре правильного многоугольника.

В отличие от вписанной окружности, общей формулы для нахождения радиуса описанной около многоугольника окружности нет. Радиус описанной окружности можно найти как радиус окружности, описанной около любого из треугольников, вершины которого являются вершинами описанного многоугольника.

Например, для описанного пятиугольника ABCDE радиус можно найти как радиус окружности, описанной около одного из треугольников ABC, ABD, ABE, BCD, BCE, ACD, ADE и т.д.

Формулы для нахождения радиуса описанной окружности существуют в частных случаях: для правильных многоугольников, треугольников, прямоугольника.

Видео:110. Окружность, описанная около правильного многоугольникаСкачать

2 Comments

Огромное спасибо за все статьи, что есть на этом сайте! Благодаря вам восполнила пробелы в теории, из-за которых не могла решить задачки, и теперь щёлкаю задания как орехи. Лучший сайт по геометрии!

Видео:9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

Вписанные многоугольники

В основном курсе геометрии доказывается, что около всякого треугольника можно описать окружность. Оказывается, для четырехугольников это уже не имеет место.

Теорема 5. Около четырехугольника можно описать окружность, тогда и только тогда, когда сумма его противоположных углов равна 180°.

Доказательство. Пусть ABCD — четырехугольник, около которого описана окружность (рис. 19, а). Докажем, что ?B + ?D = 180°. Действительно, эти углы измеряются половинами соответствующих дуг ADC и ABC, которые вместе составляют всю окружность. Следовательно, сами углы в сумме измеряются половиной дуги окружности, т.е. их сумма равна 180°.

Обратно, пусть в четырехугольнике ABCD сумма противоположных углов равна 180°. Через вершины A, B, C проведем окружность. Предположим, что эта окружность не проходит через вершину D (рис. 19, б). Обозначим точку пересечения окружности с прямой AD через D’. Тогда четырехугольник ABCD’ вписан в окружность и, следовательно, ?B +?D’=180°. Но по условию ?B +?D = 180°. Поэтому ?D =?D’, что невозможно, так как прямые DC и D’C не являются параллельными. Полученное противоречие показывает, что окружность, проходящая через точки A, B и C должна пройти и через точку D.

Теорема 6. В выпуклый четырехугольник можно вписать окружность, тогда и только тогда, когда суммы его противоположных сторон равны.

Доказательство. Пусть ABCD — четырехугольник, в который вписана окружность, касающаяся его сторон в точках M, N, P, Q (рис. 20, а). Дока­жем, что AB + CD = BC + AD. Действительно, из равенства отрезков касательных, проведенных к окружности из одной точки следуют равенства: AM = AQ, BM = BN, CN = CP, DP = DQ. Поэтому, AB + CD = AM + MB + CP + PD = AQ + QD + BN + NC = AD + BC.

Обратно, пусть в выпуклом четырехугольнике ABCD выполняется равенство AB + CD = BC + AD. Покажем, что в него можно вписать окружность. Для этого достаточно проверить, что биссектрисы углов этого четырехугольника пересекаются в одной точке. Эта точка будет равноудалена от всех сторон четырехугольника и, следовательно, будет центром искомой вписанной окружности. Если в данном четырехугольнике выполняется равенство AB=BC, то этот четырехугольник ромб. Ясно, что биссектрисы углов ромба пересекаются в одной точке — точке пересечения его диагоналей. Пусть ABBC. Предположим для определенности AB > BC (рис. 20, б). Из условия AB + CD = BC + AD следует, что AB — BC = AD — CD. Возьмем на AB точку E так, что BE=BC. Тогда AE = AB-BC. Возьмем на AD точку F так, что DF=DC. Тогда AF = AD — CD. Следовательно, AE=AF.

Треугольники AEF, BCE, CDF — равнобедренные. Поэтому биссектрисы углов A, B, D являются серединными перпендикулярами к отрезкам EF, EC, CF. Следовательно, они пересекаются в одной точке — центре окружности, описанной около треугольника EFC. Эта точка будет равноудалена от всех сторон исходного четырехугольника, т.е. будет искомым центром вписанной окружности.

Теорема Птолемея для четырехугольника, вписанного в окружность, утверждает, что произведение его диагоналей равно сумме произведений противоположных сторон. Мы докажем более сильную теорему.

Теорема 7. Произведение диагоналей произвольного четырехугольника меньше или равно сумме произведений его противоположных сторон, причем равенство достигается только в случае четырехугольника, вписанного в окружность.

Доказательство. Пусть ABCD — четырехугольник. Воспользуемся инверсией с центром в точке A и радиусом R (рис. 21). Напомним, что при инверсии точкам X, отличным от A, сопоставляются точки X’ на луче AX, для которых При этом окружности, не проходящие через точку A, переходят в окружности, а окружности, проходящие через точку A, за исключением самой точки A, переходят в прямые.

Пусть точки B, C и D переходят соответственно в точки B’, C’ и D’. Тогда треугольники ABC и A’C’B’, ADC и AC’D’, ABD и AD’B’ подобны и, следовательно, имеют место равенства

Складывая почленно эти равенства, получим

Следовательно, имеет место неравенство

При этом, равенство достигается только в случае, когда точки B’, C’, D’ принадлежат одной прямой. Это выполняется только в случае, если точки B, C, D принадлежат окружности, проходящей через точку A.

Рассмотрим теперь пятиугольники, вписанные в окружность.

Теорема 8. Сумма любых двух несмежных углов вписанного пятиугольника больше 180°.

Доказательство следует из того, что углы A и C пятиугольника ABCDE опираются на дуги, в сумме составляющие всю окружность плюс дугу DE (рис. 22).

Естественный вопрос, который возникает после этого — является полученное условие достаточным для того, чтобы около пятиугольника можно было описать окружность?

Пример такого пятиугольника легко построить. Возьмем какой-нибудь вписанный пятиугольник ABCDE (рис. 23) и, продолжая две его стороны, построим пятиугольник ABCD’E’ так, чтобы сторона D’E’ была параллельна DE. Тогда углы этого пятиугольника будут равны углам исходного, и около него нельзя описать окружность.

Поставим другой вопрос, связанный с достаточным условием вписанности пятиугольника. Пусть ABCDE — пятиугольник, сумма любых двух несмежных углов которого больше 180°. Существует ли пятиугольник A’B’C’D’E’ с такими же углами, около которого можно описать окружность?

Прежде чем ответить на этот вопрос выразим углы между диагоналями вписанного пятиугольника ABCDE, выходящими из одной вершины через углы самого пятиугольника.

Легко видеть, что ?CAD = ?B + ?E — 180°. Аналогичным образом выражаются и другие углы (рис. 24).

Вернемся теперь к поставленному вопросу. Для ответа на него рассмотрим какую-нибудь окружность и разделим ее на дуги, равные удвоенным углам между диагоналями исходного пятиугольника, выходящим из одной вершины. Концы этих дуг будут вершинами искомого пятиугольника вписанного в окружность.

Таким образом, имеет место следующая теорема.

Теорема 9. Для произвольного пятиугольника ABCDE, суммы любых двух несмежных углов которого больше 180°, существует пятиугольник A’B’C’D’E’ с такими же углами, около которого можно описать окружность.

Ситуация с вписанными в окружность семиугольниками, девятиугольниками и т. д. аналогична рассмотренной ситуации с пятиугольниками.

Для вписанных многоугольников с четным числом сторон ситуация аналогична ситуации с вписанным четырехугольником.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Нахождение радиуса описанной вокруг правильного многоугольника окружности

В публикации представлена формула, с помощью которой можно найти радиус окружности, описанной около правильного многоугольника, а также приведен пример решения задачи для лучшего понимания представленного материала.

Видео:Построение пятиугольника циркулем и линейкойСкачать

Формула расчета радиуса окружности

На рисунке изображен правильный шестиугольник с описанной вокруг него окружностью, но формула ниже подходит для любого правильного n-угольника.

где a – длина стороны.

Примечание: зная радиус описанного круга можно найти сторону равностороннего n-угольника (формула выводится из представленной выше):

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Пример задачи

Дан правильный пятиугольник с длиной стороны 8 см. Вычислите радиус описанной около данной фигуры окружности.

Решение:
Применим соответствующую формулу, подставив в нее известное нам значение.

🎦 Видео

Окружность, описанная около правильного многоугольника | Геометрия 7-9 класс #105 | ИнфоурокСкачать

Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

Формулы радиусов описанной и вписанной окружностей правильного многоугольника 2Скачать

Вписанная и описанная окружность - от bezbotvyСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Построение пятиугольника циркулемСкачать

9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать

ПОСТРОИТЬ ПРАВИЛЬНЫЙ ПЯТИУГОЛЬНИК [construction a regular pentagon]Скачать

Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

ЗАДАЧА ПРО ПЯТИУГОЛЬНИКСкачать

Описанная окружностьСкачать

Задача 6 №27916 ЕГЭ по математике. Урок 133Скачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Правильный многоугольник. Окружность, описанная около правильного многоугольника.Скачать