Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.
Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
Квадрат касательной равен произведению секущей на ее внешнюю часть
Центральный угол — это угол, вершина которого совпадает с центром окружности.
Дугой называется часть окружности, заключенная между двумя точками.
Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.
Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.
Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.
Периметр сектора: P = s + 2R.
Площадь сектора: S = Rs/2 = ПR 2 а/360°.
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.
Видео:5 класс, 22 урок, Окружность и кругСкачать

Вопросы и тест к зачету по теме «Окружность»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Видео:Окружность. Круг. 5 класс.Скачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»
Сертификат и скидка на обучение каждому участнику
Вопросы к зачету по теме «Окружность»
Взаимное расположение прямой и окружности (все случаи в зависимости от соотношения между радиусом окружности и расстоянием от центра окружности до прямой). Секущая.
Касательная к окружности, определение. Свойство касательной. Признак касательной.
Теорема об отрезках касательных, проведенных из одной точки к окружности.
Построение касательной к окружности, проведенной через данную точку (два случая: точка лежит на окружности и точка – вне окружности).
Определение центрального и вписанного углов.
Градусная мера дуги, обозначение, измерение.
Теорема о величине вписанного угла (рассмотреть 3 случая).
Свойство вписанных углов, опирающихся на одну и ту же дугу (хорду).
Теорема о свойстве отрезков двух пересекающихся хорд окружности.
Четыре замечательные точки треугольника.
Теорема о точке пересечения биссектрис треугольника. Теорема о вписанной в треугольник окружности.
Теорема о точке пересечения высот треугольника – ортоцентре.
Теорема о точке пересечения медиан треугольника – центре тяжести.
Серединный перпендикуляр к отрезку и его свойство. Теорема о точке пересечения серединных перпендикуляров к сторонам треугольника. Теорема об описанной около треугольника окружности.
Вписанные и описанные многоугольники ( определения).
Теорема об описанном около окружности четырехугольнике (прямая и обратная).
Теорема о вписанном в окружность четырехугольнике (прямая и обратная).
Построение среднего пропорционального двух отрезков.
Теорема об отрезках касательной и секущей, проведенных из одной точки к окружности.
Теорема об отрезках секущих, проведенных из одной точки к окружности.
Теорема об угле между касательной и секущей, проведенных через одну точку окружности.
Теоремы об измерении углов с вершиной вне и внутри окружности.
Тест к зачету по теме «окружность»
Прямая и окружность имеют две общие точки, если расстояние от _________________________ до______________ _________меньше ___________________________.
Могут ли две касательные к одной окружности быть параллельными?___________________
Если прямая АВ – касательная к окружности с центром О и В – точка касания, то прямая АВ и _____________ ОВ _______________________________________________
Верно ли, что градусная мера дуги окружности может быть больше 180 градусов?___________
Верно ли, что если сумма градусных мер двух дуг окружности равна 360 градусам, то эти дуги имеют общие концы?___________
Могут ли вписанные углы, опирающиеся на одну и ту же дугу, не быть равными?___________
Определите, является ли треугольник АВМ остроугольным, прямоугольным или тупоугольным, если точки А и В – концы диаметра окружности, а точка М лежит на окружности?__________________
Определите, является ли вписанный угол АВС острым, прямым или тупым, если точка Р лежит на дуге АВС и угол АРС – острый?____________________________
Может ли градусная мера центрального угла быть меньше градусной меры соответствующей ему дуги?_________________________
Если вписанный угол опирается на диаметр, то __________________________________
Если угол ABD – вписанный, а AOD – центральный, то ABD = —- AOD .
Если отрезки АВ и АТ отрезки касательных к окружности, то __________________________________
Если хорды AB и CD пересекаются в точке Е, то верно равенство:_____________
Если AB — касательная, AD – секущая и АМ — ее внешняя часть, то справедливо равенство:___________________________________________
Центром окружности, вписанной в треугольник, является точка___________________________________________________________________
Если точка равноудалена от сторон угла, то она лежит на _____________________________________
Если точка лежит на серединном перпендикуляре, проведенном к данному отрезку, то она_____________________________________________________________________
Около любого ___________________________можно описать окружность. Ее центром является точка пересечения_____________________________ , т.к. она равноудалена от __________________________
Точка пересечения ________________ треугольника делит их в отношении _________, считая от _________________
Если центром вписанной в треугольник окружности является точка пересечения медиан, то этот треугольник а) прямоугольный, б) равнобедренный, в) равносторонний
Определите вид треугольника, если центр описанной окружности лежит на одной из его сторон._____________________________
Определите вид треугольника, если точка пересечения его высот совпадает с вершиной треугольника __________________________
Определите, около какого параллелограмма ( не являющегося квадратом) всегда можно описать окружность_________________________
Определите, каким свойством должны обладать диагонали прямоугольника, чтобы в него можно было вписать окружность___________________________________________________________
Каким свойством должен обладать четырехугольник, чтобы около него можно было описать окружность?______________________________________________________________________
Если в четырехугольник ABCD вписана окружность, то_____________________________
Треугольник вписан в окружность. Определите его вид, если ни одна из его сторон не больше диаметра окружности____________________________________________
Даны две трапеции. Известно, что около первой нельзя описать окружность, а во вторую нельзя вписать окружность. Какая из этих трапеций может быть равнобедренной?__________________
Тест к зачету по теме «окружность»
Прямая и окружность имеют только одну общую точку, если расстояние от _________________________ до______________ _________равно ___________________________.
Могут ли две касательные к одной окружности быть перпендикулярными?___________________
Если прямая АВ проходит через конец радиуса ОК и АВ перпендикулярна ОК, то АВ является ______________________________ к данной окружности.
Верно ли, что градусная мера центрального угла может быть больше 180 градусов?___________
Верно ли, что если две различные дуги имеют общие концы, то сумма их градусных мер равна 360 градусам?___________
Могут ли два вписанных угла быть равными, если они опираются на разные дуги?__________________________________
Определите, является ли треугольник АВМ остроугольным, прямоугольным или тупоугольным, если АВ и АС – хорды окружности, а дуга АВС меньше полуокружности?__________________
Определите, является ли вписанный угол АВС острым, прямым или тупым, если точка Р лежит на дуге АВС и угол АРС –тупой?____________________________
Может ли градусная мера вписанного угла быть больше градусной меры соответствующей ему дуги?_________________________
Если вписанный угол опирается на диаметр, то __________________________________
Если угол AB С – вписанный, а AO С – центральный, то AB С= —- AO С.
Если хорды МР и ТК пересекаются в точке Е, то верно равенство:_____________
Если ВМ и ВТ – отрезки касательных к окружности, то________________________________________
Если ТН — касательная, ТМ– секущая и ТК — ее внешняя часть, то справедливо равенство:___________________________________________
Центром окружности, описанной около треугольника, является точка___________________________________________________________________
Если точка лежит на биссектрисе угла, то она_____________________________________
Если точка равноудалена от концов отрезка, то она лежит на __________________________________
В любой ___________________________можно вписать окружность. Ее центром является точка пересечения_____________________________ , т.к. она равноудалена от __________________________
Точка пересечения ________________ треугольника делит их в отношении _________, считая от _________________
Если центром вписанной в треугольник окружности является точка пересечения высот , то этот треугольник а) прямоугольный, б) равнобедренный, в) равносторонний
Определите вид треугольника, если центр описанной окружности лежит на одной из его сторон._____________________________
Определите вид треугольника, если точка пересечения его высот совпадает с вершиной треугольника __________________________
Определите, в какой параллелограмм ( не являющегося квадратом) всегда можно вписать окружность_________________________
Определите, каким свойством должны обладать диагонали ромба, чтобы около него можно было описать окружность___________________________________________________________
Каким свойством должен обладать четырехугольник, чтобы около него можно было описать окружность?______________________________________________________________________
Если в четырехугольник МРТК вписана окружность, то_____________________________
Треугольник вписан в окружность. Определите его вид, если диаметр окружности меньше любой из его сторон ____________________________________________
Даны две трапеции. Известно, что около первой можно описать окружность, а во вторую можно вписать окружность. Какая из этих трапеций может быть прямоугольной?__________________
Краткое описание документа:
Зачеты — форма организации контроля и учета успеваемости учащихся, они решают задачи систематизации, углубления и закрепления знаний, умений и навыков по важнейшим разделам и темам программы, готовят учащихся к сдаче итогового экзамена. Цель учителя – добиться того, чтобы каждый учащийся овладел важнейшими умениями и навыками. Поэтому, если ученик не справился с зачетом, надо организовать доработку соответствующего материала, и его повторную проверку.
Данный зачет проводится в завершении темы «Окружность» письменно на уроке и подразумевает проверку знаний теории. Практическая часть зачета предусматривается на другом уроке. Проверяются как знания базового уровня так и повышенного . Это дает возможность учителю судить о готовности или неготовности каждого ученика к дальнейшему продвижению по курсу, скорректировать дальнейшую работу, выявив учащихся с затруднениями и пробелами, а также тех, кто усвоил материал на высоком уровне; определить эффективность организации, методов и средств обучения; выявить степень правильности, объем, глубину усвоенных знаний. Зачет развивает у учащихся умение анализировать, систематизировать информацию, воспитывает серьезное отношение к обучению и формирует умение оценивать свой уровень знаний и стремление повышать его. Круг вопросов, вынесенных на зачет, и дата зачета известны учащимся задолго до проведения зачета. В ходе подготовки к зачету обсуждаются и решаются задачи разного уровня: базового и повышенного, задаются и обсуждаются дифференцированные домашние контрольные работы разного уровня сложности.
Зачет оценивается отметками от 3 до 5 или «незачтено» по количеству набранных баллов за каждый из ответов.
Видео:Окружность и круг, 6 классСкачать

Окружность и круг вопросы с ответами
Тесты по геометрии 7 класс. Тема: «Окружность»
Правильный вариант ответа отмечен знаком +
1. Радиусом окружности называется отрезок … Закончите определение:
— соединяющий две любые точки окружности
+ соединяющий центр окружности с какой-либо точкой окружности
— пересекающий окружность в двух точках
— ограничивающий дугу окружности
2. Окружность – это совокупность … точек на плоскости, которые находятся на одинаковом расстоянии от заданной точки O, которая называется центром окружности. Вставьте пропущенное слово:
3. Часть плоскости, ограниченной окружностью, называется:
4. Центр окружности – это:
— точка, делящая радиус пополам
+ точка, равноудаленная от всех точек окружности
— точка, которая находится в пределах окружности
— точка, расположенная на диаметре окружности
5. Отрезок, проходящий через две точки и центр окружности, называется:
6. Как называется прямая, имеющая одну общую точку с окружностью?
7. Какой отрезок называется хордой?
+ соединяющий 2 точки окружности
— равный двум радиусам
— разделяющий окружность на 2 равные дуги
8. Дуга окружности – это:
+ часть окружности, ограниченная хордой
— множество равноудаленных от центра окружности точек
— две точки, соединенные отрезком
— часть окружности, равная радиусу
9. Диаметр, перпендикулярный хорде… Закончите утверждение:
+ делит эту хорду и дуги, которые она стягивает, пополам
— делится хордой пополам
— равен произведению длины радиуса и хорды
— называется секущей окружности
тест 10. Если 2 хорды равны, следовательно, они… Закончите утверждение:
— проходят через центр окружности
— выходят из одной точки окружности
— пересекают друг друга
+ стягивают 2 одинаковые дуги
11. Укажите формулу диаметра окружности D:
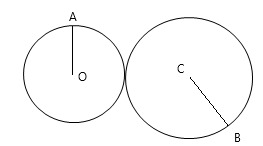
12. Две окружности пересекаются в одной точке. Радиус OA=20 см, радиус CB=30 см. Найдите расстояние между двумя центрами окружностей.
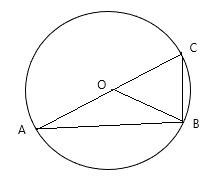
13. Дана окружность с центром O, в которую вписан треугольник ABC. Медиана треугольника OB=8 см. Чему равен диаметр окружности?
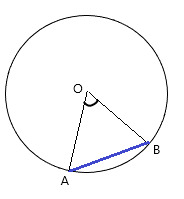
14. Дана окружность с центром О. Угол AOB=60 о , радиус OB=10 см. Найдите хорду AB.
15. Через три точки, которые не лежат на одной прямой… Закончите утверждение:
— можно провести три различных окружности
— можно провести равносторонний треугольник
+ можно провести только одну окружность
— нельзя построить параллельные прямые
16. Если две окружности соприкасаются в одной точке, то на какой прямой лежит эта точка?
+ на прямой, что проходит через центры окружностей
— на прямой, перпендикулярной радиусам окружностей
— на прямой, соединяющей центры вписанных в окружности треугольников
17. Как вычислить длину окружности через радиус?
18. Чему равно кратчайшее расстояние от центра окружности к касательной?
— квадратному корню из диаметра
— медиане вписанного треугольника
19. Секущая окружности – это:
— одна из сторон описанного треугольника
— прямая, параллельная диаметру окружности
— хорда, которая равна радиусу окружности
+ прямая, которая проходит через 2 точки окружности
тест-20. Если радиус окружности перпендикулярен к хорде, то он… Закончите утверждение:
— равен длине хорды
+ разделяет хорду пополам в точке их пересечения
— делит хорду в отношении 1:2
— делится пополам в точке пересечения с хордой
21. Что такое центральный угол окружности?
— угол, вершина которого лежит на окружности, а стороны угла пересекают окружность
— угол, равный 60 0
+ угол, вершиной которого является центр окружности
— угол, одна из сторон которого проходит через центр окружности
22. Если вписанный угол равен 90 0 , то он… Закончите утверждение:
+ опирается на диаметр
— имеет равные стороны
— имеет сторону, проходящую через центр окружности
— имеет сторону, равную радиусу
23. Как называется часть окружности, которая соединяет 2 точки на окружности?
24. Как измеряется вписанный угол?
— равен дуге, на которую он опирается
— равен центральному углу, опирающемуся на ту же дугу
+ равен половине дуги, на которую он опирается
25. Если вписанные углы опираются на одну дугу, то они… Закончите утверждение:
+ равны между собой
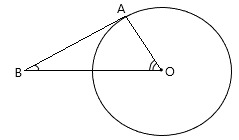
26. Дана окружность с центром O. AB – касательная к окружности. Угол ABO=33 0 , чему равен угол BOA?
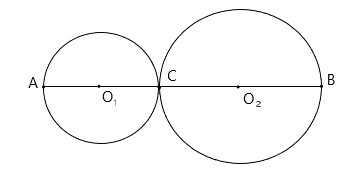
27. Даны две окружности с центрами O2 и O1, которые касаются в точке C. Радиус меньшей окружности равен 4 см, длина отрезка AB=20 см. Чему равен радиус большей окружности?
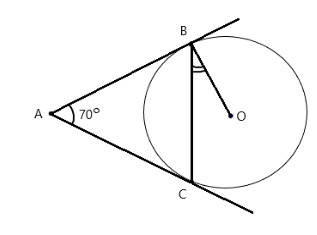
28. Лучи AB и AC касаются окружности с центром О в точках B и C. Угол BAC=70 0 . Найдите угол OBC.
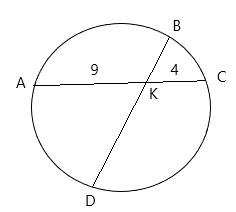
29. Найдите длину хорды BD, если AK=9 см, KC=4 см, BK:KD = 1:4.
тест_30. A – точка касания окружности с центром O и прямой AB. OA=9 см, AB=12 см. Найдите длину отрезка CB.
🔥 Видео
Всё про углы в окружности. Геометрия | МатематикаСкачать

Математика 5 класс (Урок№26 - Окружность и круг. Сфера и шар.)Скачать

Математика 3 класс (Урок№33 - Круг. Окружность (центр, радиус, диаметр)Скачать

Длина окружности. Площадь круга. 6 класс.Скачать

Окружность и круг. Центр, радиус, диаметр, хорда, дуга, сектор и длина окружности, площадь круга.Скачать

Круг. Окружность | Математика 3 класс #21 | ИнфоурокСкачать

Окружность. 7 класс.Скачать

МАТЕМАТИКА 5 класс: Окружность и кругСкачать

Окружность. Круг. Практическая часть - решение задачи. 5 класс.Скачать

Окружность и круг. Длина окружности. Площадь круга. Урок 15. Математика 6 классСкачать

Круг. Окружность (центр, радиус, диаметр)Скачать

Окружность и круг | Математика 5 класс #22 | ИнфоурокСкачать

Математика 5 Окружность КругСкачать

Видеоурок 14. Круг и окружность. Математика 3 классСкачать

Длина окружности. Практическая часть - решение задачи. 6 класс.Скачать

Чем отличается круг от окружностиСкачать
МЕРЗЛЯК-6. КРУГ И ОКРУЖНОСТЬ. ПАРАГРАФ-24Скачать