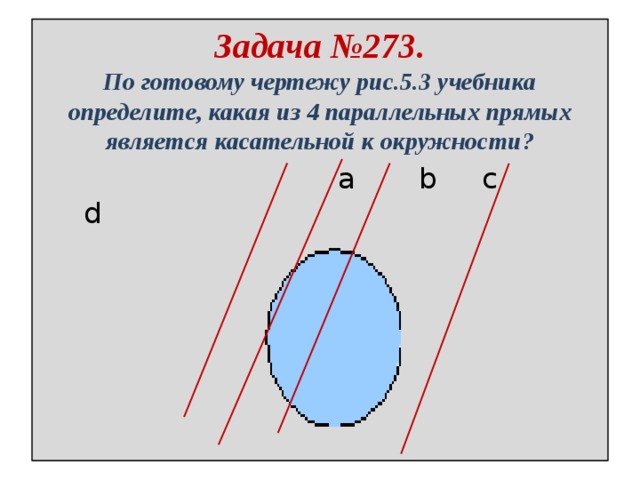
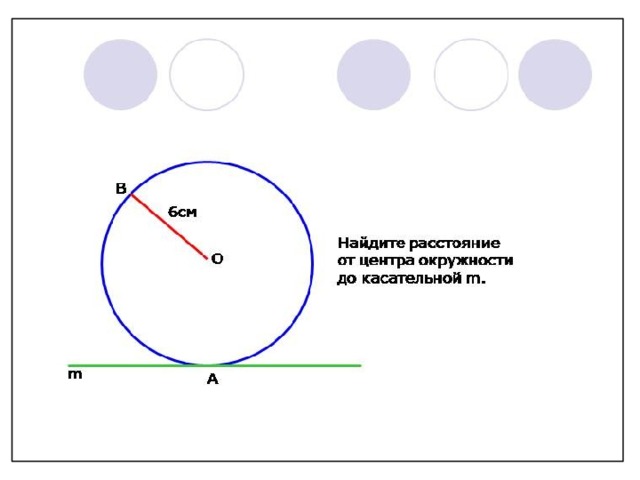
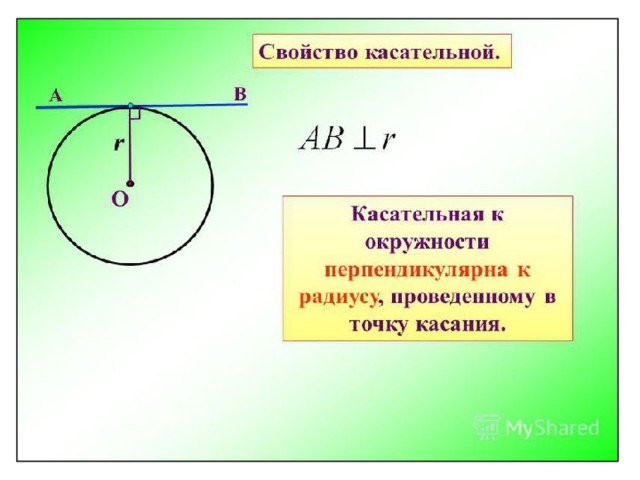
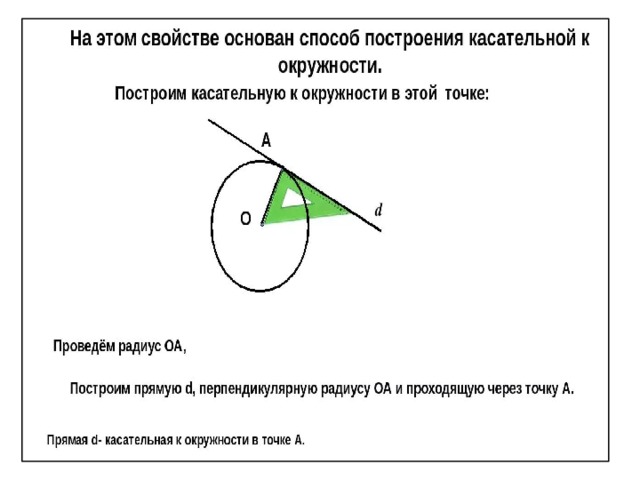
Секущие, касательные — все это сотни раз можно было слышать на уроках геометрии. Но выпуск из школы позади, проходят года, и все эти знания забываются. Что следует вспомнить?
- Сущность
- История открытия и изучения
- Свойства
- Построение
- Интересное
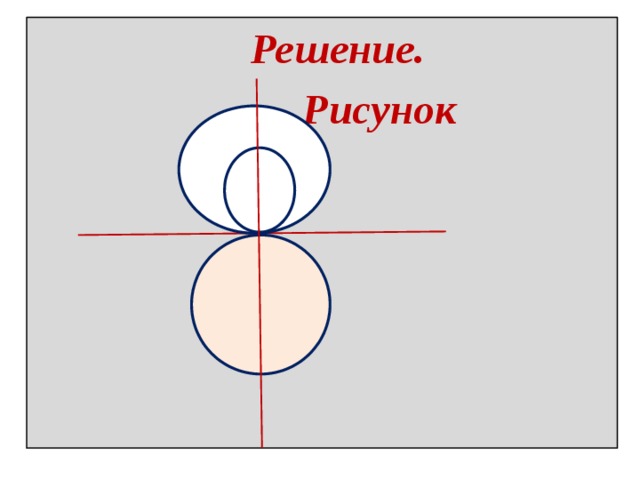
- Две окружности
- Типы и разновидности
- Решение задач
- Примеры из жизни
- Касательная к окружности
- Касательная к окружности, секущая и хорда — в чем разница
- Свойства касательной к окружности
- Задача
- Задача 1
- Задача 2
- Задача 1
- Задача 2
- Задача 1
- Задача 2
- Касательная к окружности
- Просмотр содержимого документа «Касательная к окружности»
- 📸 Видео
Видео:Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

Сущность
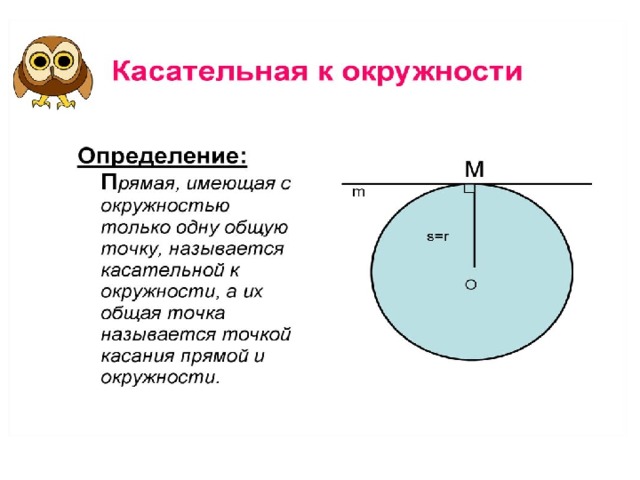
Термин «касательная к окружности» знаком, наверное, всем. Но вряд ли у всех получится быстро сформулировать его определение. Между тем касательной называют такую прямую, лежащую в одной плоскости с окружностью, которая пересекает ее только в одной точке. Их может существовать огромное множество, но все они обладают одинаковыми свойствами, о которых речь пойдет ниже. Как нетрудно догадаться, точкой касания называют то место, где окружность и прямая пересекаются. В каждом конкретном случае она одна, если же их больше, то это будет уже секущая.
Видео:8 класс, 32 урок, Касательная к окружностиСкачать

История открытия и изучения
Понятие касательной появилось еще в древности. Построение этих прямых сначала к окружности, а потом к эллипсам, параболам и гиперболам с помощью линейки и циркуля проводилось еще на начальных этапах развития геометрии. Разумеется, история не сохранила имя первооткрывателя, но очевидно, что еще в то время людям были вполне известны свойства касательной к окружности.
В Новое время интерес к этому явлению разгорелся вновь — начался новый виток изучения этого понятия в сочетании с открытием новых кривых. Так, Галилей ввел понятие циклоиды, а Ферма и Декарт построили к ней касательную. Что же касается окружностей, кажется, еще для древних не осталось секретов в этой области.
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Свойства
Радиус, проведенный в точку пересечения, будет перпендикулярен прямой. Это
Из вышесказанного есть важное следствие. Для каждой точки окружности можно построить касательную, но при этом только одну. Доказательство этого достаточно просто: теоретически опустив на нее перпендикуляр из радиуса, выясняем, что образованный треугольник существовать не может. И это значит, что касательная — единственная.
Видео:Окружность, касательная, секущая и хорда | МатематикаСкачать

Построение
Среди прочих задач по геометрии есть особая категория, как правило, не
Итак, даны окружность и точка, лежащая вне ее границ. И необходимо провести через них касательную. Как же это сделать? Прежде всего, нужно провести отрезок между центром окружности О и заданной точкой. Затем с помощью циркуля следует разделить его пополам. Чтобы это сделать, необходимо задать радиус — чуть более половины расстояния между центром изначальной окружности и данной точкой. После этого нужно построить две пересекающиеся дуги. Причем радиус у циркуля менять не надо, а центром каждой части окружности будут изначальная точка и О соответственно. Места пересечений дуг нужно соединить, что разделит отрезок пополам. Задать на циркуле радиус, равный этому расстоянию. Далее с центром в точке пересечения построить еще одну окружность. На ней будет лежать как изначальная точка, так и О. При этом будет еще два пересечения с данной в задаче окружностью. Именно они и будут точками касания для изначально заданной точки.
Видео:ОГЭ за одну минуту | ОГЭ, математика, задание 16 (окружность и касательная)Скачать

Интересное
Именно построение касательных к окружности привело к рождению
Кроме того, касательная к окружности связана с геометрическим смыслом тангенса. Именно от этого и происходит его название. В переводе с латыни tangens — «касательная». Таким образом, это понятие связано не только с геометрией и дифференциальным исчислением, но и с тригонометрией.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Две окружности
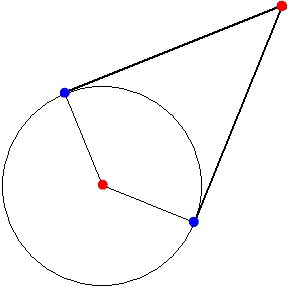
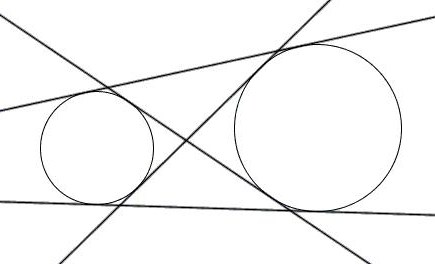
Не всегда касательная затрагивет лишь одну фигуру. Если к одной окружности можно провести огромное множество прямых, то почему же нельзя наоборот? Можно. Вот только задача в этом случае серьезно усложняется, ведь касательная к двум окружностям может проходить не через любые точки, а взаимное расположение всех этих фигур может быть очень
Видео:Касательные к окружностиСкачать

Типы и разновидности
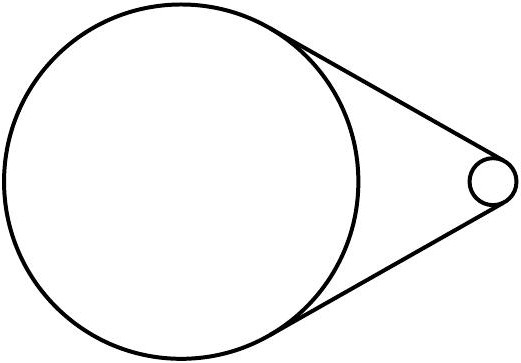
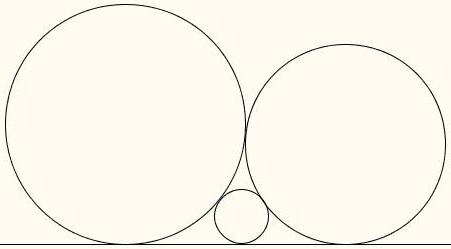
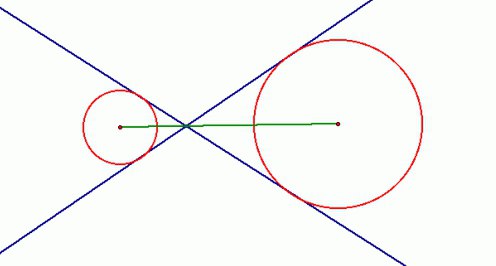
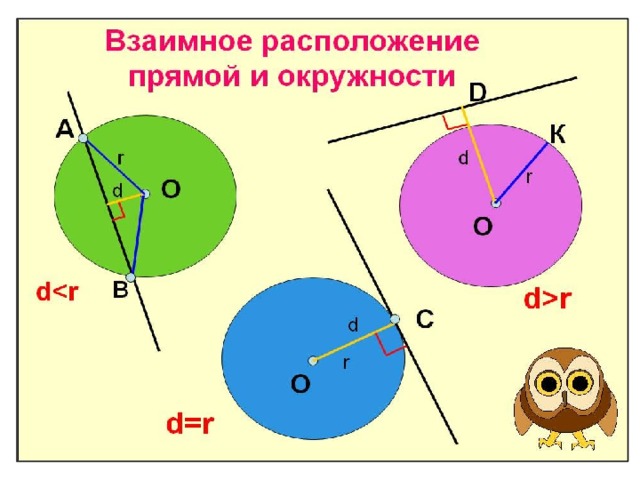
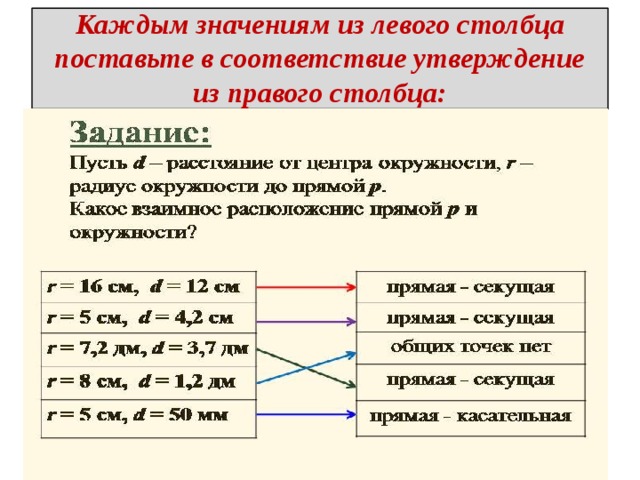
Когда речь идет о двух окружностях и одной или нескольких прямых, то даже если известно, что это касательные, не сразу становится ясно, как все эти фигуры расположены по отношению друг к другу. Исходя из этого, различают несколько разновидностей. Так, окружности могут иметь одну или две общие точки или не иметь их вовсе. В первом случае они будут пересекаться, а во втором — касаться. И вот тут различают две разновидности. Если одна окружность как бы вложена во вторую, то касание называют внутренним, если нет — то внешним. Понять взаимное расположение фигур можно не только, исходя из чертежа, но и располагая информацией о сумме их радиусов и расстоянии между их центрами. Если две эти величины равны, то окружности касаются. Если первая больше — пересекаются, а если меньше — то не имеют общих точек.
Так же и с прямыми. Для любых двух окружностей, не имеющих общих точек, можно
Если речь идет об окружностях, которые имеют одну общую точку, то задача серьезно упрощается. Дело в том, что при любом взаимном расположении в этом случае касательная у них будет только одна. И проходить она будет через точку их пересечения. Так что построение трудности не вызовет.
Если же фигуры имеют две точки пересечения, то для них может быть построена прямая, касательная к окружности как одной, так и второй, но только внешняя. Решение этой проблемы аналогично тому, что будет рассмотрено далее.
Видео:Секущая и касательная. 9 класс.Скачать

Решение задач
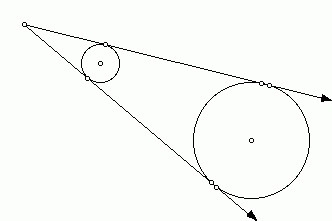
Как внутренняя, так и внешняя касательная к двум окружностям, в построении не так уж просты, хоть эта проблема и решаема. Дело в том, что для этого используется вспомогательная фигура, так что додуматься до такого способа самостоятельно
Прежде всего, около центра большей окружности нужно построить вспомогательную. При этом на циркуле должна быть установлена разница между радиусами двух изначальных фигур. Из центра меньшей окружности строятся касательные к вспомогательной. После этого из О1 и О2 проводятся перепендикуляры к этим прямым до пересечения с изначальными фигурами. Как следует из основного свойства касательной, искомые точки на обеих окружностях найдены. Задача решена, по крайнем мере, ее первая часть.
Для того чтобы построить внутренние касательные, придется решить практически
Касательная к окружности или даже двум и больше — не такая уж сложная задача. Конечно, математики давно перестали решать подобные проблемы вручную и доверяют вычисления специальным программам. Но не стоит думать, что теперь необязательно уметь делать это самостоятельно, ведь для правильного формулирования задания для компьютера нужно многое сделать и понять. К сожалению, есть опасения, что после окончательного перехода на тестовую форму контроля знаний задачи на построение будут вызывать у учеников все больше трудностей.
Что же касается нахождения общих касательных для большего количества окружностей, это не всегда возможно, даже если они лежат в одной плоскости. Но в некоторых случаях можно найти такую прямую.
Видео:Окружность №16 из ОГЭ. Свойства хорд, касательных, секущих.Скачать

Примеры из жизни
Общая касательная к двум окружностям нередко встречается и на практике, хоть это и не всегда заметно. Конвейеры, блочные системы, передаточные ремни шкивов, натяжение нити в швейной машинке, да даже просто велосипедная цепь — все это примеры из жизни. Так что не стоит думать, что геометрические задачи остаются лишь в теории: в инженерном деле, физике, строительстве и многих других областях они находят практическое применение.
Видео:Урок по теме КАСАТЕЛЬНАЯ К ОКРУЖНОСТИСкачать

Касательная к окружности
О чем эта статья:
Видео:Доказательство того, что радиус перпендикулярен касательной | Окружность | ГеометрияСкачать

Касательная к окружности, секущая и хорда — в чем разница
В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.