Около трапеции описана окружность центр которой лежит внутри трапеции

Геометрия | 5 — 9 классы

Около трапеции описана окружность, центр которой лежит внутри трапеции ; Высота трапеции = 27 ; Основания = 48 и 30 ; Найти радиус окружности.

И если не затруднит, то с объяснениями, пожалуйста).

Около трапеции описана окружность — значит, трапеция вписанная и равнобедренная, т.

К. в окружность можно вписать только равнобедренную трапецию.

Сделаем рисунок, обозначим вершины углов трапеции привычными АВСДЧерез центр окружности проведем перпендикулярно к основаниям трапеции диаметр.

Его отрезок МК, заключенный между основаниями трапеции, является ее высотой и делит основания пополам.

( Основания — хорды, перпендикуляр из центра окружности к хорде делит ее пополам).

Соединим центр О с вершинами С и Д.

Обозначим ОК = х, тогда ОМ = 27 — х

R² = КД² + ОК² Приравняем значения радиуса.

225 + (27 — х)² = 576 + х²

Видео:Около трапеции описана окружностьСкачать

В окружность радиуса 41 вписана трапеция, основания которой равны 18 и 80, причем центр окружности лежит внутри трапеции?

В окружность радиуса 41 вписана трапеция, основания которой равны 18 и 80, причем центр окружности лежит внутри трапеции.

Найдите высоту этой трапеции.

Видео:Основания равнобедренной трапеции равны 72 и 30. Центр окружности, описанной около трапеции... (ЕГЭ)Скачать

В окружность радиуса 41 вписана трапеция, основания которой равны 18 и 80, причем центр окружности лежит внутри трапеции?

В окружность радиуса 41 вписана трапеция, основания которой равны 18 и 80, причем центр окружности лежит внутри трапеции.

Найдите высоту этой трапеции.

Видео:Задача про трапецию, описанную около окружностиСкачать

В окружность радиуса 41 вписана трапеция, основания которой равны 18 и 80 , причем центр окружности лежит внутри трапеции?

В окружность радиуса 41 вписана трапеция, основания которой равны 18 и 80 , причем центр окружности лежит внутри трапеции.

Найдите высоту этой трапеции.

Видео:Задание 6 ЕГЭ по математике #157Скачать

Около трапеции с основаниями 48 и 30 описана окружность?

Около трапеции с основаниями 48 и 30 описана окружность.

Найти её радиус, если высота трапеции 27.

Видео:Геометрия Равнобокая трапеция вписана в окружность, центр которой принадлежит одному из основанияСкачать

Около трапеции с высотой 8 описана окружность, центр которой лежит внутри трапеции?

Около трапеции с высотой 8 описана окружность, центр которой лежит внутри трапеции.

Большее основание трапеции видно из центра окружности под углом 110 * , а меньшее под углом 70 * .

Найдите плорщадь трапеции.

Видео:Радиус описанной окружности трапецииСкачать

В равнобедренной трапеции длины оснований равны 14 см и 40 см, а длина высоты — 9 см?

В равнобедренной трапеции длины оснований равны 14 см и 40 см, а длина высоты — 9 см.

Найдите радиус окружности, описанной около этой трапеции.

Известно, что центр окружности лежит внутри трапеции.

Видео:Задача 6 №27926 ЕГЭ по математике. Урок 141Скачать

Центр окружности радиуса R, описанной около трапеции, лежит на одном из оснований?

Центр окружности радиуса R, описанной около трапеции, лежит на одном из оснований.

Найдите периметр трапеции, если один из ее углов равен 60.

Видео:ЕГЭ математика 2023 Вариант 2 задача 1Скачать

Основания равнобедренной трапеции равны 32 и 24?

Основания равнобедренной трапеции равны 32 и 24.

Радиус описанной окружности равен 20.

Центр окружности лежит внутри трапеции.

Найдите высоту трапеции.

Видео:Где центр окружности? ТрапецияСкачать

В равнобедренной трапеции длины оснований равны 6 см и 4 см, а длина высоты — 4 см?

В равнобедренной трапеции длины оснований равны 6 см и 4 см, а длина высоты — 4 см.

Найдите радиус окружности, описанной около этой трапеции.

Известно, что центр окружности лежит внутри трапеции.

Видео:ЕГЭ ПЛАНИМЕТРИЯ ОПИСАННАЯ ОКРУЖНОСТЬ ОКОЛО РАВНОБЕДРЕННОЙ ТРАПЕЦИИ | ТЕЛЕМОСТ НАПРЯМУЮ С ТРАПЕЦИЕЙСкачать

Центр окружности радиуса R, описанной около трапеции, лежит на одном из оснований?

Центр окружности радиуса R, описанной около трапеции, лежит на одном из оснований.

Найдите периметр трапеции, если один из ее углов равен 60.

Вы перешли к вопросу Около трапеции описана окружность, центр которой лежит внутри трапеции ; Высота трапеции = 27 ; Основания = 48 и 30 ; Найти радиус окружности?. Он относится к категории Геометрия, для 5 — 9 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Геометрия. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.

Возможно, кому — то пригодится решение — привожу своё : Пусть BC = AD = aBC = AD = a, тогда из условия BP = a / 4, PC = 3a / 4, AQ = 2a / 5, QD = 3a / 5BP = a / 4, PC = 3a / 4, AQ = 2a / 5, QD = 3a / 5. MOMO и ONON найдём как средние линии трапеций ..

Решение 22см — одна из сторон, т. К. сумма от точки пересекч к соседним сторонам равна одной стороне. 22 — 6 = 16см — вторая сторона.

Х + х — 6 = 22 2х — 6 = 22 2х = 22 + 6 2х = 28 х = 28 / 2 х = 14 одна сторона это Х то есть 14 а вторая х — 6 то есть 14 — 6 = 8.

1) вектор а = 2i — j 2) координаты вектора c .

Вот, пожалуйста✩ ^ _ ^ Все очень просто решается по теореме Пифагора.

Решение задания приложено.

ВС = MB — MC = 18, 2 — 9, 4 = 8, 8 Ответ : 1.

1). треугольники КВА = КАD по 2 — ум сторонам и углу между ними, т. К. АD = АВ (ABCD ромб), КА — общая, углы КАВ = КАD. 2) Из равенства треугольников следует что КВ = КD.

3 и 4 не могут существовать, т. К у треугольника сумма любых двух сторон должна быть больше третьей.

Примем коэффициент подобия стороны треугольника за — х, значит : ▪одна сторона — 4х ▪ вторая сторона — 6х ▪ третья сторона — 7х ▪периметр треугольника это сумма всех его сторон, а т. К. тругольники подобные, значит стороны одного треуг. Соответстве..

Видео:Трапеция и вписанная окружностьСкачать

Задача 17558 Основания равнобедренной трапеции равны.

Условие

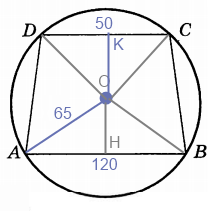
Основания равнобедренной трапеции равны 120 и 50. Центр окружности, описанной около трапеции, лежит внутри трапеции, а радиус окружности равен 65. Найдите высоту трапеции.

Решение

Высота трапеции в данном случае есть ничто иное, как сумма высот двух равнобедренных треугольников AOB и DOC, опущенных на их основания AB и DC соответственно.

OA = OB = DO = OC = r = 65.
AH = AB/2 = 120/2 = 60.

[b]Перейдем к вычислениям.[/b]

Высота треугольника AOB вычисляется по теореме Пифагора:

OH = sqrt(AO^2-AH^2) = sqrt(65^2-60^2) = 25

Аналогично для высоты треугольника DOC

OK = sqrt(65^2-25^2) = 60

Следовательно высота трапеции равно KH = OH + OK = 25+60 = 85.

[b]Ответ:[/b] 85

Видео:Трапеция в окружности. Задача Шаталова.Скачать

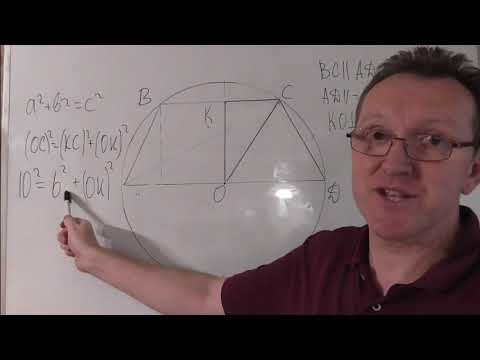
Около трапеции описана окружность центр которой лежит внутри трапеции

Вопрос по геометрии:

Около трапеции описана окружность, центр которой лежит внутри трапеции; Высота трапеции = 27; Основания = 48 и 30; Найти радиус окружности.
И если не затруднит, то с объяснениями, пожалуйста)

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Около трапеции описана окружность — значит, трапеция вписанная и равнобедренная, т.к. в окружность можно вписать только равнобедренную трапецию.
Сделаем рисунок, обозначим вершины углов трапеции привычными АВСД Через центр окружности проведем перпендикулярно к основаниям трапеции диаметр.
Его отрезок МК, заключенный между основаниями трапеции, является ее высотой и делит основания пополам. ( Основания — хорды, перпендикуляр из центра окружности к хорде делит ее пополам).
Соединим центр О с вершинами С и Д.
ОС=ОД=R
Обозначим ОК=х, тогда ОМ =27-х
По т. Пифагора
R²=МС²+ОМ²
R²=КД²+ОК² Приравняем значения радиуса.
МС²+ОМ²=КД²+ОК²
225+(27-х)²=576+х²
54х=378
х=7
ОК=7
R²=КД²+ОК²
R²=24²+7²
R²=625
R=25

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

🎬 Видео

Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

Окружность, вписанная в трапециюСкачать

Боковые стороны трапеции, описанной около окружности, равны 13 и 1. Найдите среднюю линию трапеции.Скачать

11.43.1. Планиметрия. Гордин Р.К.Скачать

Планиметрия 27 | mathus.ru | окружность, касающаяся основания трапеции и вписанной в нее окружностиСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Окружность и трапеция | ЕГЭ-2018. Задание 16. Математика. Профильный уровень | Борис Трушин +Скачать