Курс школьной геометрии » Окружность

Около прямоугольника можно описать окружность доказательство

Обновлено
Описанная окружность

Окружность описанная около многоугольника — это окружность, на которой лежат все вершины многоугольника. Вписанный в окружность многоугольник — это многоугольник, все вершины которого лежат на окружности. На рисунке 1 четырехугольник АВСD вписан в окружность с центром О, а четырехугольник АЕСD не является вписанным в эту окружность, так как вершина Е не лежит на окружности.

Около прямоугольника можно описать окружность доказательство

Теорема

Около любого треугольника можно описать окружность.
Содержание
  1. Доказательство
  2. Доказательство
  3. Доказательство
  4. Доказательство
  5. Доказательство
  6. Прямоугольник. Онлайн калькулятор
  7. Свойства прямоугольника
  8. Диагональ прямоугольника
  9. Окружность, описанная около прямоугольника
  10. Формула радиуса окружности описанной около прямоугольника
  11. Периметр прямоугольника
  12. Формулы сторон прямоугольника через его диагональ и периметр
  13. Признаки прямоугольника
  14. Описанная и вписанная окружность
  15. теория по математике 📈 планиметрия
  16. Описанная окружность
  17. Вписанная окружность
  18. Вписанный и описанный треугольники
  19. Вписанный и описанный четырехугольники
  20. 🎬 Видео

Доказательство

Дано: произвольный Около прямоугольника можно описать окружность доказательствоАВС.

Доказать: около Около прямоугольника можно описать окружность доказательствоАВС можно описать окружность.

Доказательство:

1. Проведем серединные перпендикуляры к сторонам Около прямоугольника можно описать окружность доказательствоАВС, которые пересекутся в точке О (по свойству серединных перпендикуляров треугольника). Соединим точку О с точками А, В и С (Рис. 2).

Около прямоугольника можно описать окружность доказательство

Точка О равноудалена от вершин Около прямоугольника можно описать окружность доказательствоАВС (по теореме о серединном перпендикуляре), поэтому ОА = ОВ = ОС. Следовательно, окружность с центром О радиуса ОА проходит через все три вершины треугольника, значит, является описанной около Около прямоугольника можно описать окружность доказательствоАВС. Теорема доказана.

Замечание 1

Около треугольника можно описать только одну окружность.

Доказательство

Предположим, что около треугольника можно описать две окружности. Тогда центр каждой из них равноудален от его вершин и поэтому совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника. Следовательно, эти окружности совпадают, т.е. около треугольника можно описать только одну окружность. Что и требовалось доказать.

Замечание 2

Около четырехугольника не всегда можно описать окружность.

Доказательство

Рассмотрим, например, ромб, не являющийся квадратом. Такой ромб можно «поместить» в окружность так, что две его вершины будут лежать на этой окружности (Рис. 3), но нельзя «поместить» ромб в окружность так, чтобы все его вершины лежали на окружности, т.к. диаметр окружности, равный одной из диагоналей ромба, будет больше (меньше) второй диагонали, т.е. нельзя описать окружность. Что и требовалось доказать.

Около прямоугольника можно описать окружность доказательство

Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:

В любом вписанном четырехугольнике сумма противоположных углов равна 180 0 .

Доказательство

Рассмотрим четырехугольник АВСD, вписанный в окружность (Рис. 4).

Около прямоугольника можно описать окружность доказательство

Углы В и D — вписанные, тогда по теореме о вписанном угле: Около прямоугольника можно описать окружность доказательствоВ = Около прямоугольника можно описать окружность доказательствоОколо прямоугольника можно описать окружность доказательствоАDС, Около прямоугольника можно описать окружность доказательствоD = Около прямоугольника можно описать окружность доказательствоОколо прямоугольника можно описать окружность доказательствоАВС, откуда следует Около прямоугольника можно описать окружность доказательствоВ + Около прямоугольника можно описать окружность доказательствоD = Около прямоугольника можно описать окружность доказательствоОколо прямоугольника можно описать окружность доказательствоАDС + Около прямоугольника можно описать окружность доказательствоОколо прямоугольника можно описать окружность доказательствоАВС = Около прямоугольника можно описать окружность доказательство(Около прямоугольника можно описать окружность доказательствоАDС + Около прямоугольника можно описать окружность доказательствоАВС). Дуги АDС и АВС вместе составляют окружность, градусная мера которой равна 360 0 , т.е. Около прямоугольника можно описать окружность доказательствоАDС + Около прямоугольника можно описать окружность доказательствоАВС = 360 0 , тогда Около прямоугольника можно описать окружность доказательствоВ + Около прямоугольника можно описать окружность доказательствоD = Около прямоугольника можно описать окружность доказательствоОколо прямоугольника можно описать окружность доказательство360 0 = 180 0 . Что и требовалось доказать.

Верно и обратное утверждение:

Если сумма противоположных углов четырехугольника равна 180 0 , то около него можно описать окружность.

Доказательство

Дано: четырехугольник АВСD, Около прямоугольника можно описать окружность доказательствоBАD + Около прямоугольника можно описать окружность доказательствоBСD = 180 0 .

Доказать: около АВСD можно описать окружность.

Доказательство:

Проведем окружность через три вершины четырехугольника: А, В и D (Рис. 5), — и докажем, что она проходит также через вершину С, т.е. является описанной около четырехугольника АВСD.

Около прямоугольника можно описать окружность доказательство

Предположим, что это не так. Тогда вершина С лежит либо внутри круга, либо вне его.

Рассмотрим первый случай, когда точка С лежит внутри круга (Рис. 6).

Около прямоугольника можно описать окружность доказательство

Около прямоугольника можно описать окружность доказательствоВСD — внешний угол Около прямоугольника можно описать окружность доказательствоСFD, следовательно, Около прямоугольника можно описать окружность доказательствоBСD = Около прямоугольника можно описать окружность доказательствоВFD + Около прямоугольника можно описать окружность доказательствоFDE. (1)

Углы ВFD и FDE — вписанные. По теореме о вписанном угле Около прямоугольника можно описать окружность доказательствоВFD = Около прямоугольника можно описать окружность доказательствоОколо прямоугольника можно описать окружность доказательствоВАD и Около прямоугольника можно описать окружность доказательствоFDE = Около прямоугольника можно описать окружность доказательствоОколо прямоугольника можно описать окружность доказательствоЕF, тогда, подставляя данные равенства в (1), получим: Около прямоугольника можно описать окружность доказательствоBСD = Около прямоугольника можно описать окружность доказательствоОколо прямоугольника можно описать окружность доказательствоВАD + Около прямоугольника можно описать окружность доказательствоОколо прямоугольника можно описать окружность доказательствоЕF = Около прямоугольника можно описать окружность доказательство(Около прямоугольника можно описать окружность доказательствоВАD + Около прямоугольника можно описать окружность доказательствоЕF), следовательно, Около прямоугольника можно описать окружность доказательствоВСDОколо прямоугольника можно описать окружность доказательствоОколо прямоугольника можно описать окружность доказательствоОколо прямоугольника можно описать окружность доказательствоВАD.

Около прямоугольника можно описать окружность доказательствоBАD — вписанный, тогда по теореме о вписанном угле Около прямоугольника можно описать окружность доказательствоBАD = Около прямоугольника можно описать окружность доказательствоОколо прямоугольника можно описать окружность доказательствоВЕD, тогда Около прямоугольника можно описать окружность доказательствоBАD + Около прямоугольника можно описать окружность доказательствоBСDОколо прямоугольника можно описать окружность доказательствоОколо прямоугольника можно описать окружность доказательство(Около прямоугольника можно описать окружность доказательствоВЕD + Около прямоугольника можно описать окружность доказательствоВАD).

Дуги ВЕD и ВАD вместе составляют окружность, градусная мера которой равна 360 0 , т.е. Около прямоугольника можно описать окружность доказательствоВЕD + Около прямоугольника можно описать окружность доказательствоВАD = 360 0 , тогда Около прямоугольника можно описать окружность доказательствоBАD + Около прямоугольника можно описать окружность доказательствоBСDОколо прямоугольника можно описать окружность доказательствоОколо прямоугольника можно описать окружность доказательствоОколо прямоугольника можно описать окружность доказательство360 0 = 180 0 .

Итак, мы получили, что Около прямоугольника можно описать окружность доказательствоBАD + Около прямоугольника можно описать окружность доказательствоBСDОколо прямоугольника можно описать окружность доказательство180 0 . Но это противоречит условию Около прямоугольника можно описать окружность доказательствоBАD + Около прямоугольника можно описать окружность доказательствоBСD =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность.

Рассмотрим второй случай, когда точка С лежит вне круга (Рис. 7).

Около прямоугольника можно описать окружность доказательство

По теореме о сумме углов треугольника в Около прямоугольника можно описать окружность доказательствоВСF: Около прямоугольника можно описать окружность доказательствоС + Около прямоугольника можно описать окружность доказательствоВ + Около прямоугольника можно описать окружность доказательствоF = 180 0 , откуда Около прямоугольника можно описать окружность доказательствоС = 180 0 — ( Около прямоугольника можно описать окружность доказательствоВ + Около прямоугольника можно описать окружность доказательствоF). (2)

Около прямоугольника можно описать окружность доказательствоВ — вписанный, тогда по теореме о вписанном угле Около прямоугольника можно описать окружность доказательствоВ = Около прямоугольника можно описать окружность доказательствоОколо прямоугольника можно описать окружность доказательствоЕF. (3)

Около прямоугольника можно описать окружность доказательствоF и Около прямоугольника можно описать окружность доказательствоВFD — смежные, поэтому Около прямоугольника можно описать окружность доказательствоF + Около прямоугольника можно описать окружность доказательствоВFD = 180 0 , откуда Около прямоугольника можно описать окружность доказательствоF = 180 0 — Около прямоугольника можно описать окружность доказательствоВFD = 180 0 — Около прямоугольника можно описать окружность доказательствоОколо прямоугольника можно описать окружность доказательствоВАD. (4)

Подставим (3) и (4) в (2), получим:

Около прямоугольника можно описать окружность доказательствоС = 180 0 — (Около прямоугольника можно описать окружность доказательствоОколо прямоугольника можно описать окружность доказательствоЕF + 180 0 — Около прямоугольника можно описать окружность доказательствоОколо прямоугольника можно описать окружность доказательствоВАD) = 180 0 — Около прямоугольника можно описать окружность доказательствоОколо прямоугольника можно описать окружность доказательствоЕF — 180 0 + Около прямоугольника можно описать окружность доказательствоОколо прямоугольника можно описать окружность доказательствоВАD = Около прямоугольника можно описать окружность доказательство(Около прямоугольника можно описать окружность доказательствоВАD — Около прямоугольника можно описать окружность доказательствоЕF), следовательно, Около прямоугольника можно описать окружность доказательствоСОколо прямоугольника можно описать окружность доказательствоОколо прямоугольника можно описать окружность доказательствоОколо прямоугольника можно описать окружность доказательствоВАD.

Около прямоугольника можно описать окружность доказательствоА — вписанный, тогда по теореме о вписанном угле Около прямоугольника можно описать окружность доказательствоА = Около прямоугольника можно описать окружность доказательствоОколо прямоугольника можно описать окружность доказательствоВЕD, тогда Около прямоугольника можно описать окружность доказательствоА + Около прямоугольника можно описать окружность доказательствоСОколо прямоугольника можно описать окружность доказательствоОколо прямоугольника можно описать окружность доказательство(Около прямоугольника можно описать окружность доказательствоВЕD + Около прямоугольника можно описать окружность доказательствоВАD). Но это противоречит условию Около прямоугольника можно описать окружность доказательствоА + Около прямоугольника можно описать окружность доказательствоС =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность. Что и требовалось доказать.

Примечание:

Окружность всегда можно описать:

Поделись с друзьями в социальных сетях:

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Окружность вписанная в треугольник и описанная около треугольника.

Прямоугольник. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ прямоугольника, радиус описанной вокруг прямоугольника окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Прямоугольник − это параллелограмм, у которого все углы прямые (Рис.1).

Около прямоугольника можно описать окружность доказательство

Можно дать и другое определение прямоугольника.

Определение 2. Прямоугольник − это четырехугольник, у которого все углы прямые.

Видео:№709. Докажите, что если около параллелограмма можно описать окружность, то этот параллелограммСкачать

№709. Докажите, что если около параллелограмма можно описать окружность, то этот параллелограмм

Свойства прямоугольника

Так как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника.

  • 1. Стороны прямоугольника являются его высотами.
  • 2. Все углы прямоугольника прямые.
  • 3. Квадрат диагонали прямоугольника равен сумме квадратов его соседних двух сторон.
  • 4. Диагонали прямоугольника равны.
  • 5. Около любого прямоугольника можно описать окружность, при этом диаметр описанной окружности равна диагонали прямоугольника.

Длиной прямоугольника называется более длинная пара его сторон.

Шириной прямоугольника называется более короткая пара его сторон.

Видео:№708. Докажите, что можно описать окружность: а) около любого прямоугольника; б) около любойСкачать

№708. Докажите, что можно описать окружность: а) около любого прямоугольника; б) около любой

Диагональ прямоугольника

Определение 3. Диагональ прямоугольника − это отрезок, соединяющий две несмежные вершины прямоугольника.

Около прямоугольника можно описать окружность доказательство

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. Прямоугольник имеет две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

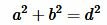Около прямоугольника можно описать окружность доказательство
Около прямоугольника можно описать окружность доказательство.(1)

Из равенства (1) найдем d:

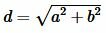Около прямоугольника можно описать окружность доказательство.(2)

Пример 1. Стороны прямоугольника равны Около прямоугольника можно описать окружность доказательство. Найти диагональ прямоугольника.

Решение. Для нахождения диаметра прямоугольника воспользуемся формулой (2). Подставляя Около прямоугольника можно описать окружность доказательствов (2), получим:

Около прямоугольника можно описать окружность доказательство

Ответ: Около прямоугольника можно описать окружность доказательство

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Вписанная и описанная окружность - от bezbotvy

Окружность, описанная около прямоугольника

Определение 4. Окружность называется описанной около прямоугольника, если все вершины прямоугольника находятся на этой окружности (Рис.3):

Около прямоугольника можно описать окружность доказательство

Видео:№710. Докажите, что если около трапеции можно описать окружность, то эта трапеция равнобедренная.Скачать

№710. Докажите, что если около трапеции можно описать окружность, то эта трапеция равнобедренная.

Формула радиуса окружности описанной около прямоугольника

Выведем формулу вычисления радиуса окружности, описанной около прямоугольника через стороны прямоугольника.

Нетрудно заметить, что радиус описанной около прямоугольника окружности равна половине диагонали (Рис.3). То есть

( small R=frac )(3)

Подставляя (3) в (2), получим:

( small R=frac<large sqrt> )(4)

Пример 2. Стороны прямоугольника равны Около прямоугольника можно описать окружность доказательство. Найти радиус окружности, описанной вокруг прямоугольника.

Решение. Для нахождения радиуса окружности описанной вокруг прямоугольника воспользуемся формулой (4). Подставляя Около прямоугольника можно описать окружность доказательствов (4), получим:

Около прямоугольника можно описать окружность доказательство
Около прямоугольника можно описать окружность доказательство

Ответ: Около прямоугольника можно описать окружность доказательство

Видео:Геометрия Известно, что около четырехугольника ABCD можно описать окружность и что продолжениеСкачать

Геометрия Известно, что около четырехугольника ABCD можно описать окружность и что продолжение

Периметр прямоугольника

Определение 5. Периметр прямоугольника − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Периметр прямоугольника вычисляется формулой:

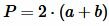Около прямоугольника можно описать окружность доказательство(5)

где ( small a ) и ( small b ) − стороны прямоугольника.

Пример 3. Стороны прямоугольника равны Около прямоугольника можно описать окружность доказательство. Найти периметр прямоугольника.

Решение. Для нахождения периметра прямоугольника воспользуемся формулой (5). Подставляя Около прямоугольника можно описать окружность доказательствов (5), получим:

Около прямоугольника можно описать окружность доказательство

Ответ: Около прямоугольника можно описать окружность доказательство

Видео:Геометрия Докажите, что если около ромба можно описать окружность, то этот ромб является квадратомСкачать

Геометрия Докажите, что если около ромба можно описать окружность, то этот ромб является квадратом

Формулы сторон прямоугольника через его диагональ и периметр

Выведем формулу вычисления сторон прямоугольника, если известны диагональ ( small d ) и периметр ( small P ) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие ( small frac P2>d ) (это следует из неравенства треугольника).

Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:

Около прямоугольника можно описать окружность доказательство(6)
Около прямоугольника можно описать окружность доказательство(7)

Из формулы (7) найдем ( small b ) и подставим в (6):

Около прямоугольника можно описать окружность доказательство(8)
Около прямоугольника можно описать окружность доказательство(9)

Упростив (4), получим квадратное уравнение относительно неизвестной ( small a ):

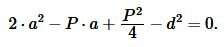Около прямоугольника можно описать окружность доказательство(10)

Вычислим дискриминант квадратного уравнения (10):

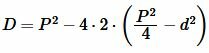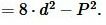Около прямоугольника можно описать окружность доказательствоОколо прямоугольника можно описать окружность доказательство(11)

Сторона прямоугольника вычисляется из следующих формул:

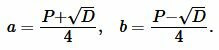Около прямоугольника можно описать окружность доказательство(12)

После вычисления ( small a ), сторона ( small b ) вычисляется или из формулы (12), или из (8).

Примечание. Легко можно доказать, что

( frac

>d ; ⇒ ; P>2cdot d ; ⇒ ) ( small P^2>4 cdot d^2 ; ⇒ ; 4d^2-P^2 2d .) Следовательно выполняется неравенство (*).

Пример 4. Диагональ прямоугольника равна Около прямоугольника можно описать окружность доказательство, а периметр равен Около прямоугольника можно описать окружность доказательство. Найти стороны прямоугольника.

Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант ( small D ) из формулы (11). Для этого подставим Около прямоугольника можно описать окружность доказательство, Около прямоугольника можно описать окружность доказательствов (11):

Около прямоугольника можно описать окружность доказательство

Подставляя значения Около прямоугольника можно описать окружность доказательствои Около прямоугольника можно описать окружность доказательствов первую формулу (12), получим:

Около прямоугольника можно описать окружность доказательство

Найдем другую сторону ( small b ) из формулы (8). Подставляя значения Около прямоугольника можно описать окружность доказательствои Около прямоугольника можно описать окружность доказательствов формулу, получим:

Около прямоугольника можно описать окружность доказательство

Ответ: Около прямоугольника можно описать окружность доказательство, Около прямоугольника можно описать окружность доказательство

Видео:Как узнать, что около четырехугольника можно описать окружность?😍 #математика #математикаегэ #егэСкачать

Как узнать, что около четырехугольника можно описать окружность?😍 #математика #математикаегэ #егэ

Признаки прямоугольника

Признак 1. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.

Признак 2. Если квадрат диагонали параллелограмма равен сумме квадратов его смежных сторон, то этот параллелограмм является прямоугольником.

Признак 3. Если углы параллелограмма равны, то этот параллелограмм является прямоугольником.

Видео:#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая Эйлера

Описанная и вписанная окружность

теория по математике 📈 планиметрия

Видео:Вокруг любого треугольника можно описать окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Вокруг любого треугольника можно описать окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРА

Описанная окружность

Окружность называется описанной вокруг многоугольника, если все вершины многоугольника принадлежат этой окружности. Многоугольник в этом случае называется вписанным в окружность.

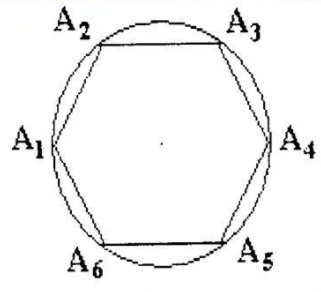
Любой правильный многоугольник можно вписать в окружность. На рисунке описанная окружность проходит через каждую вершину правильного шестиугольника.

Около прямоугольника можно описать окружность доказательство

Видео:9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

9 класс, 22 урок, Окружность, описанная около правильного многоугольника

Вписанная окружность

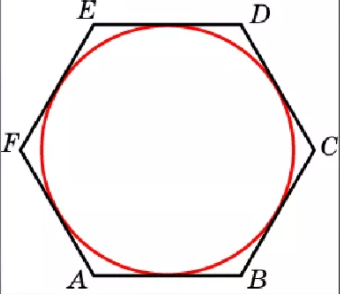
Окружность называется вписанной в многоугольник, если она касается всех его сторон. Многоугольник в этом случае называется описанным около окружности.

В любой правильный многоугольник можно вписать окружность. На рисунке окружность вписана в правильный шестиугольник, она касается всех его сторон.

Около прямоугольника можно описать окружность доказательство

Вписанный и описанный треугольники

Центр описанной около треугольника окружности лежит на пересечении серединных перпендикуляров, проведенных к сторонам треугольника.

В любой треугольник можно вписать окружность: 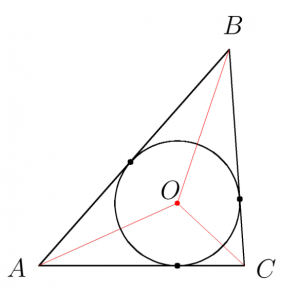Около прямоугольника можно описать окружность доказательствоЦентр вписанной окружности

Центр окружности, вписанной в треугольник, лежит на пересечении его биссектрис.

Вписанный и описанный четырехугольники

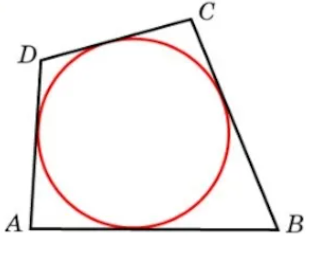
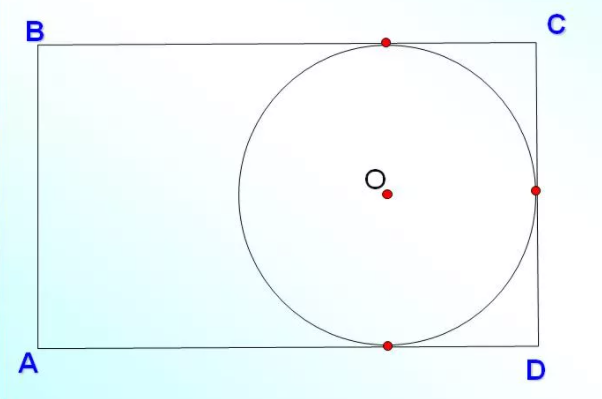
Не во всякий четырехугольник можно вписать окружность. Например, в прямоугольник нельзя вписать окружность. По рисунку видно, что окружность касается только трех его сторон, что не соответствует определению.

Около прямоугольника можно описать окружность доказательствоУсловие вписанной в 4-х угольник окружности

Окружность является вписанной в четырехугольник, если суммы длин противоположных сторон равны.

Около прямоугольника можно описать окружность доказательство

На рисунке выполняется данное условие, то есть AD + BC=DC + AB

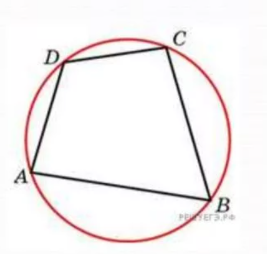
Окружность является описанной около четырехугольника, если суммы противоположных углов равны 180 градусов.

Около прямоугольника можно описать окружность доказательство

На рисунке окружности описана около четырехугольника, следовательно выполнено условие, что сумма углов А и С равна сумме углов B и D и равна 180 градусов.

🎬 Видео

Геометрия Можно ли описать окружность около четырехугольника ABCD если AB = 4 см AD = 3 см BD = 6смСкачать

Геометрия Можно ли описать окружность около четырехугольника ABCD если AB = 4 см AD = 3 см BD = 6см

Геометрия 8 класс (Урок№33 - Описанная окружность.)Скачать

Геометрия 8 класс (Урок№33 - Описанная окружность.)

Если в четырёхугольник можно вписать окружностьСкачать

Если в четырёхугольник можно вписать окружность

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnline

Геометрия Найдите диагональ AC четырехугольника ABCD если около него можно описать окружность и ABСкачать

Геометрия Найдите диагональ AC четырехугольника ABCD если около него можно описать окружность и AB

5 Описанная окружность около четырехугольника. СвойствоСкачать

5 Описанная окружность около четырехугольника. Свойство

Всё про углы в окружности. Геометрия | МатематикаСкачать

Всё про углы в окружности. Геометрия | Математика

8 класс, 39 урок, Описанная окружностьСкачать

8 класс, 39 урок, Описанная окружность

Построить описанную окружность (Задача 1)Скачать

Построить описанную окружность (Задача 1)
Поделиться или сохранить к себе: