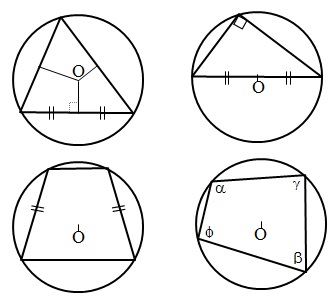
Огэ треугольник вписан в окружность (2 видео)

Огэ треугольник вписан в окружность

Задание 17. Треугольник ABC вписан в окружность с центром в точке О. Точки О и С лежат в одной полуплоскости относительно прямой АВ. Найдите угол АСВ, если угол АОВ равен 73°.

Угол AOB является центральным, так как точка O – центр окружности, следовательно, градусная мера дуги AB равна также 167°. Угол ACB является вписанным в окружность углом и опирается на дугу AB. Известно, что величина вписанного угла равна половине градусной меры дуги, на которую он опирается, то есть

Содержание

Вписанные треугольники в окружность огэ
Треугольник вписанный в окружность
Определение
Формулы
Радиус вписанной окружности в треугольник
Радиус описанной окружности около треугольника
Площадь треугольника
Периметр треугольника
Сторона треугольника
Средняя линия треугольника
Высота треугольника
Свойства
Доказательство
Вписанные треугольники в окружность огэ
Задание №16 ОГЭ по математике
Теория к заданию №16
Материал для подготовки к ОГЭ по геометрии по теме:»Центральные и вписанные углы»
Выберите документ из архива для просмотра:
📸 Видео

Видео:ОГЭ по математике. Треугольник вписан в окружность . (Вар. 4) √ 17 модуль геометрия ОГЭСкачать

Вписанные треугольники в окружность огэ

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Треугольник вписанный в окружность

Видео:ОГЭ 2023. РАЗБОР ЗАДАНИЯ №16 "Окружность"Скачать

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Видео:Задание 16 (В1) ОГЭ по математике ▶ №11 (Минутка ОГЭ)Скачать

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

Площадь треугольника вписанного в окружность,
если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = frac ab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

Периметр треугольника вписанного в окружность,
если известны все стороны:

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

Сторона треугольника вписанного в окружность,
если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

Средняя линия треугольника вписанного
в окружность, если известно основание:

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

Высота треугольника вписанного в окружность,
если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Видео:16 задача ОГЭ: четырёхугольник, вписанный в окружность; подобные треугольникиСкачать

Свойства

Центр вписанной в треугольник окружности
находится на пересечении биссектрис.
В треугольник, вписанный в окружность,
можно вписать окружность, причем только одну.
Для треугольника, вписанного в окружность,
справедлива Теорема Синусов, Теорема Косинусов
и Теорема Пифагора.
Центр описанной около треугольника окружности
находится на пересечении серединных перпендикуляров.
Все вершины треугольника, вписанного
в окружность, лежат на окружности.
Сумма всех углов треугольника — 180 градусов.
Площадь треугольника вокруг которого описана окружность, и
треугольника, в который вписана окружность, можно найти по
формуле Герона.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

Проведем серединные
перпендикуляры — HO, FO, EO.
O — точка пересечения серединных
перпендикуляров равноудалена от
всех вершин треугольника.
Центр окружности — точка пересечения
серединных перпендикуляров — около
треугольника описана окружность — O,
от центра окружности к вершинам можно
провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

Видео:Задание 16 ОГЭ по математике. Окружность вписана в равносторонний треугольник.Скачать

Вписанные треугольники в окружность огэ

Центральный угол AOB опирается на хорду AB длиной 6. При этом угол OAB равен 60°. Найдите радиус окружности.

Рассмотрим треугольник AOB: он равнобедренный, его боковые стороны равны радиусу.

Углы при основании равнобедренного треугольника равны. Пусть AOB равен x, тогда x + 60° + 60° = 180°, где x = 60°. Треугольник, у которого все углы равны, — равносторонний треугольник; значит, радиус равен 6.

В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 30°. Найдите величину угла OAB.

Вписанные углы ВСD и ВАD опираются на одну и ту же дугу окружности, поэтому они равны. Тем самым, угол OAB = 30°.

Найдите градусную меру центрального &angle;MON, если известно, NP — диаметр, а градусная мера &angle;MNP равна 18°.

Треугольник MON — равнобедренный. Тогда &angle;MON = 180° − 2·18° = 144°.

Найдите &angle;DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно.

Дуга FD, не содержащая точку Е, равна 360° − 150° − 68° = 142°, поэтому &angle;DEF = 71°.

Найдите градусную меру &angle;ACB, если известно, что BC является диаметром окружности, а градусная мера центрального &angle;AOC равна 96°.

Так как &angle;AOC и &angle;AOB — смежные, &angle;AOB = 180° − &angle;AOC = 84°. Центральный угол равен дуге, на которую он опирается, поэтому градусная мера дуги AB равна 84°. Угол ACB — вписанный и равен половине дуги, на которую опирается, поэтому &angle;ACB = 42°.

Приведем решение Артура Ахметьянова.

Треугольник AOC равнобедренный, поскольку AO = OC как радиусы окружности, тогда

Видео:Углы в окружности. 16 задание ОГЭ математика 2023 | Молодой РепетиторСкачать

Задание №16 ОГЭ по математике

В 16 задании ОГЭ по математике необходимо решить простую задачу по геометрии. Для успешного решения необходимо обладать базовыми знаниями по геометрии вообще, так как сложно выделить какую-то одну тему, по которой даны задания. Это относится ко всему модулю геометрии. Я рекомендую повторить понятия центральные и вписанные углы, свойства касательных к окружности, взаимосвязь между радиусом описанной или вписанной окружности в геометрические фигуры — в первую очередь прямоугольный треугольник и квадрат.

Теория к заданию №16

Несмотря на то, что в задании №16 могут потребоваться любые знания по геометрии, в данном разделе мы разберем теорию по теме «окружность».

Начнем рассмотрение с понятия вписанная окружность:

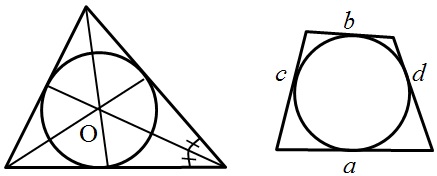
Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.
Если окружность вписана в произвольный четырехугольник, тогда попарные суммы противолежащих сторон равны между собой: a + b = c + d

Длинна окружности и площадь: Касательная и секущая:

Касательная – прямая, имеющая с окружностью одну общую точку.
Секущая – прямая, имеющая с окружностью две общие точки.

Описанная окружность и её свойства:

Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к его трем сторонам.
Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы.
Около трапеции можно описать окружность только тогда, когда трапеция равнобочная.
Если окружность описана около произвольного четырехугольника, тогда попарные суммы противолежащих углов равны между собой.

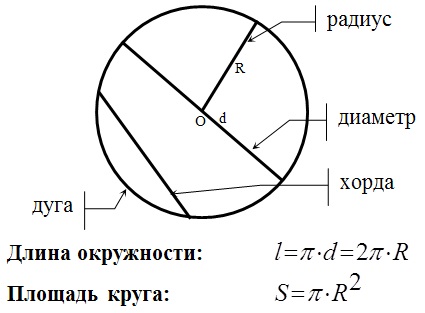
Хорда – отрезок, соединяющий две точки окружности.

Диаметр, делящий хорду пополам, перпендикулярен хорде.
В окружности равные хорды равноудалены от центра окружности.
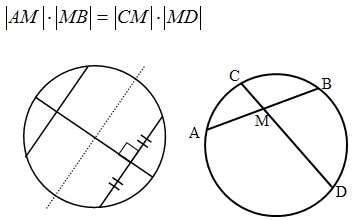
Отрезки пересекающихся хорд связаны равенством:

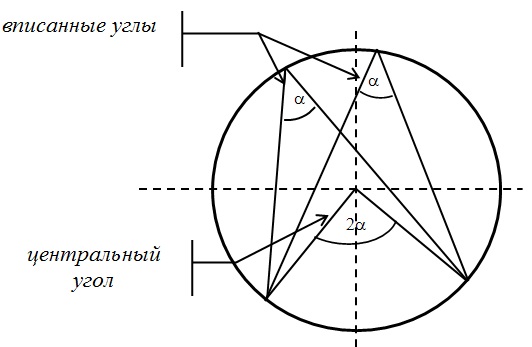
Центральный и вписанный углы:

Ниже я разобрал три различных примера 10 задания. Если у вас остались пожелания, или вы хотите разобрать задачу, которой здесь нет, напишите об этом в комментарии.

Внимательно посмотрим на рисунок. Угол ABC опирается на дугу ADC, а угол CAD — на дугу DC. Угол, который нам необходимо найти — ABD, опирается на дугу AD — которая является частью дуги ADC за вычетом дуги DC. Значит, угол ABD равен разности углов ABC и CAD:

∠ABD = 92 — 60 = 32

pазбирался: Даниил Романович | обсудить разбор | оценить

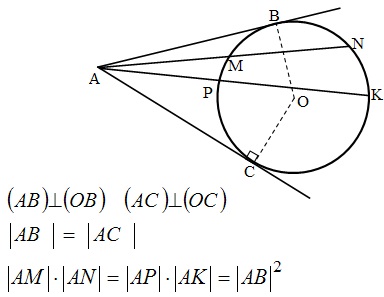
Во-первых, касательные равны между собой по длине, а значит треугольник с основанием AB равнобедренный. Угол при вершине этого треугольника равен 2 градуса по условию, значит углы при основании равны:

Во-вторых, касательные перпендикулярны радиусу, то есть угол между ними и радиусом равен 90 градусов.

Заметим, что угол ABO, который необходимо найти, является частью угла между касательной и радиусом, а именно за вычетом угла, который мы нашли в первом пункте. Значит, этот угол равен:

pазбирался: Даниил Романович | обсудить разбор | оценить

Для решения необходимо вспомнить, что центр описанной около прямоугольного треугольника окружности расположен в середине гипотенузы. То есть гипотенуза является диаметром, а её половина — радиусом.

По теореме Пифагора найдем гипотенузу AB:

AB² = BC² + AC² = 12² + 16² = 144 + 256 = 400

Гипотенуза равна 20, значит радиус — 10.

pазбирался: Даниил Романович | обсудить разбор | оценить

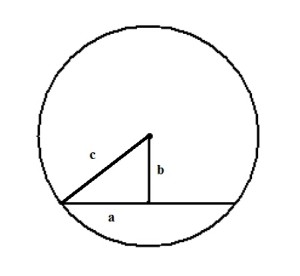
Для решения данной задачи необходимо провести радиус окружности к точке начала хорды:

Получаем прямоугольный треугольник, где гипотенуза c — радиус и равна 13 см, b — расстояние до хорды — 5 см. По теореме Пифагора находим катет a: a² + b² = c² a² = c² — b² = 13² — 5² = 169 — 25 = 144 Откуда а = √144 = 12 Но а — лишь половина хорды, поэтому вся

Хорда — длинный эластичный продольный тяж у хордовых животных; осевой скелет их предковых и некоторых современных форм. Тянется вдоль тела ниже центральной нервной системы и выше полости тела.

pазбирался: Даниил Романович | обсудить разбор | оценить

Сторона АВ треуг-ка АСВ является диаметром окружности. Это означает, что угол АСВ опирается на диаметр. Тогда угол АСВ равен 90 0 , и, следовательно, ∆АСВ прямоугольный. Если ∆АСВ прямоугольный, то для нахождения одной из его сторон можно применить т.Пифагора. По т.Пифагора

АС 2 +ВС 2 =АВ 2 (1)

По условию АС=16, радиус окружности R=10. Если R=10, то АВ=2R=2·10=20. Тогда из (1) получим: 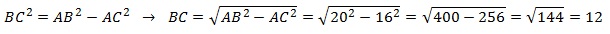Ответ: 12

pазбирался: Даниил Романович | обсудить разбор | оценить

Поскольку вершина О угла АОВ лежит в центре окружности, значит, этот угол центральный. А если так, то он равен величине дуги АВ. Т.е. ᴗАВ=113 0 . Угол АСВ является вписанным. Следовательно, его величина равна половине дуги, на которую он опирается. Из рисунка видно, что оба угла (АОВ и АСВ) опираются на одну и ту же дугу. Т.к. ᴗАВ=113 0 , то угол АСВ равен

0,5 · ᴗАВ = 0,5 · 113 0 = 56,5 0 .

pазбирался: Даниил Романович | обсудить разбор | оценить

Радиус вписанной в квадрат окружности равен 22 √ 2 . Найти диагональ этого квадрата.

Для начала надо сделать построения на чертеже, чтобы увидеть, как располагаются известные и неизвестные элементы и чем они еще могут являться на чертеже.

Обозначим диагональ АВ, точкой О – центр окружности, С – один из углов квадрата. Покажем расстояние от центра окружности до стороны квадрата – радиус r. Если радиус равен 22 √ 2 , то сторона квадрата будет в два раза больше, т.е. 44 √ 2 .

Рассмотрим прямоугольный треугольник АВС, который является равнобедренным (так как по условию дан квадрат) и боковые стороны равны по 44 √ 2 . Нам надо найти диагональ, т.е. гипотенузу данного треугольника. Вспомним, что для нахождения гипотенузы равнобедренного треугольника есть формула с=а √ 2 , где с – гипотенуза, а – катет. Подставим в неё наши данные:

с=44 √ 2 × √ 2 =44 √ 4 =44 × 2=88

pазбирался: Даниил Романович | обсудить разбор | оценить

Видео:Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать

Материал для подготовки к ОГЭ по геометрии по теме:»Центральные и вписанные углы»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Литература.docx

1.Федеральный институт педагогических измерений. Открытый банк заданий ОГЭ 2016.

2.Математика экспресс — подготовка ОГЭ 2016 Ф. Ф. Лысенко, С. Ю. Кулабухова. Легион Ростов – на – Дону.

3.Математика подготовка к ОГЭ -2016 40 тренировочных вариантов

Ф. Ф. Лысенко, С. Ю. Кулабухова. Легион Ростов – на – Дону.

4.Математика ОГЭ тематические тестовые задания 15 вариантов

С. С. Минаев, Н. Б. Мельникова. Москва 2016 «Экзамен».

Выбранный для просмотра документ аналоги1.docx

Тематический тренажёр для подготовки к ОГЭ по геометрии по теме «Вписанные и центральные углы».

Составила Грефенштейн Нина Николаевна МБОУ СОШ №7

ADA70A Т очка О – центр окружности, ∠ AOB =130° (см. рисунок). Найдите величину угла ACB (в градусах).

Точка О — центр окружности, ∠ BOC = 160 ° (см. рисунок). Найдите величину угла BAC (в градусах).

Точка О – центр окружности, ∠ AOB =84° (см. рисунок). Найдите величину угла ACB (в градусах).

Треугольник ABC вписан в окружность с центром
в точке O . Точки O и C лежат в одной полуплоскости относительно прямой AB . Найдите угол ACB , если угол AOB равен 67° . Ответ дайте в градусах.

вписан в окружность с центром
в точке O . Точки O и C лежат в одной полуплоскости относительно прямой AB . Найдите угол ACB , если угол AOB равен 113° . Ответ дайте в градусах.

вписан в окружность с центром
в точке O . Точки O и C лежат в одной полуплоскости относительно прямой AB . Найдите угол ACB , если угол AOB равен 47° . Ответ дайте в градусах.

Треугольник ABC вписан в окружность с центром
в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 167°. Ответ дайте в градусах.

Треугольник ABC вписан в окружность с центром
в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 59°. Ответ дайте в градусах.

Треугольник ABC вписан в окружность с центром
в точке O . Точки O и C лежат в одной полуплоскости относительно прямой AB . Найдите угол ACB , если угол AOB равен 73° . Ответ дайте в градусах.

Треугольник ABC вписан в окружность с центром
в точке O . Точки O и C лежат в одной полуплоскости относительно прямой AB . Найдите угол ACB , если угол AOB равен 115° . Ответ дайте в градусах.

Треугольник ABC вписан в окружность с центром
в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 173°. Ответ дайте в градусах.

Треугольник ABC вписан в окружность с центром
в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 153°. Ответ дайте в градусах.

Точка O — центр окружности, на которой лежат точки A , B и C . Известно, что ∠ ABC =69° и ∠ OAB =48° .
Найдите угол BCO . Ответ дайте в градусах.

Точка O — центр окружности, на которой лежат точки A, B и C. Известно, что ∠ ABC=71° и ∠ OAB=22°.
Найдите угол BCO. Ответ дайте в градусах.

Точка O — центр окружности, на которой лежат точки A , B и C . Известно, что ∠ ABC =61° и ∠ OAB =8° .
Найдите угол BCO . Ответ дайте в градусах.

Точка O — центр окружности, на которой лежат точки A , B и C . Известно, что ∠ ABC =76° и ∠ OAB =33° .
Найдите угол BCO . Ответ дайте в градусах.

Выбранный для просмотра документ ответы.docx

Выбранный для просмотра документ пояснительная записка.docx

Тематический тренажёр для подготовки к ОГЭ по геометрии по теме «Вписанные и центральные углы».

Составила Грефенштейн Нина Николаевна МБОУ СОШ №7

Пособие предназначено для подготовки девятиклассников к основному государственному экзамену, но может быть полезно уже, начиная с четвёртой четверти, в 8 классе. При подготовке к ОГЭ в 9 классе следует учесть, что для успешной сдачи экзаменов необходимо повторить весь материал, изучаемый в основной школе, который включает в себя 27 тем, одна из которых по геометрии «Вписанные и описанные окружности».

Учителю при подготовке к уроку, приходится тратить, много времени для выбора заданий по данной теме из различных источников. Данный тренажёр поможет учителю и ученикам.

Пособие состоит из нескольких частей:

Оно может быть использовано на уроке. Например, используя тренажёр, учащиеся могут выполнить большое число заданий базового уровня по определённой теме. При работе с хорошо успевающими учащимися, тренажёр может быть использован для самостоятельной отработки практических навыков по решению заданий. При работе со слабоуспевающими учащимися позволяет рассмотреть решение задач базового уровня, где простым языком изложены методы решения задач по данной теме всех типов встречающихся на экзамене. Тематический тренажёр может быть использован также и для самостоятельной подготовки к ОГЭ, для домашних работ, для организации диагностики и контроля ( самоконтроля), решить, а затем проверить правильность решения с помощью ответов. Если ответы не совпадут, следует ещё раз решить задачу, а при необходимости найти подобную среди разобранных примеров. Тренажёр может быть полезен также при изучении методов решения задач более сложного уровня.

Предлагаю Вашему вниманию задания по теме : «Центральные и вписанные углы».

Воспользовавшись тренажёром можно развить навыки безошибочного решения заданий первой части экзамена по данной теме и сэкономить время для решения более сложных задач.