Одна окружность вписана в прямоугольную трапецию, а вторая касается большей боковой стороны и продолжений оснований.
а) Докажите, что расстояние между центрами окружностей равно большей боковой стороне трапеции.
б) Найдите расстояние от вершины одного из прямых углов трапеции до центра второй окружности, если точка касания первой окружности с большей боковой стороной трапеции делит её на отрезки, равные 2 и 50.
а) Пусть O — центр окружности, вписанной в прямоугольную трапецию ABCD с основаниями AD и BC, O1 — центр окружности, касающейся большей боковой стороны и продолжений оснований трапеции (рис. 1).
Точка O лежит на биссектрисах углов BCD и ADC, следовательно,
Точка O1 лежит на биссектрисе угла, смежного с углом BCD, значит, Аналогично, углы CO1D и ODO1 — прямые. Значит, OCO1D — прямоугольник, поэтому CD = OO1.
б) Пусть окружность, вписанная в трапецию ABCD, касается стороны AD в точке P, а стороны CD — в точке M, вторая окружность касается прямой AD в точке Q (рис. 2).
Радиусы окружностей OP и O1Q равны половине расстояния между параллельными прямыми AD и BC. Получаем, что OO1QP — прямоугольник, следовательно, OO1 = PQ.
В прямоугольном треугольнике COD имеем:
В прямоугольном треугольнике AQO1 имеем:
Расстояние от вершины прямого угла трапеции до центра второй окружности равно
Ответ:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Содержание
Видео:Геометрия В прямоугольную трапецию вписана окружность. Точка касания делит большую боковую сторонуСкачать  Одна окружность вписана в прямоугольную трапецию, а вторая касается большей боковой стороны и продолжений оснований 1)Доказать, что расстояние между центрами окружностей равно большей боковой стороне ?Геометрия | 5 — 9 классы Одна окружность вписана в прямоугольную трапецию, а вторая касается большей боковой стороны и продолжений оснований 1)Доказать, что расстояние между центрами окружностей равно большей боковой стороне трапеции 2)Найти расстояние от вершины одного из прямых углов трапеции до центра второй окружности, если точка касания первой окружности с большей боковой стороной делит ее на отрезки , равные 2 и 50. Распишите пожалуйста подробно! Окружности будут равные, т. К. их диаметры равны, как отрезки параллельных прямых, заключенные между параллельными основаниями трапеции)) центры окружностей расположены на биссектрисах соотв углов : CO1, DO1, CO2, DO2 CO1 _|_ DO1 как биссектрисы углов, сумма которых = 180 градусов))) аналогично CO2 _|_ DO2 CO2DO1 — — прямоугольник, диагонали прямоугольника равны : CD = O1O2 радиус окружностей можно найти из прямоугольного треугольника, построив еще одну высоту трапеции))) отрезки касательных к окружности, проведенныхиз одной точки, равны))). Видео:Геометрия В прямоугольную трапецию вписана окружность. Найдите её радиус, если основания трапецииСкачать 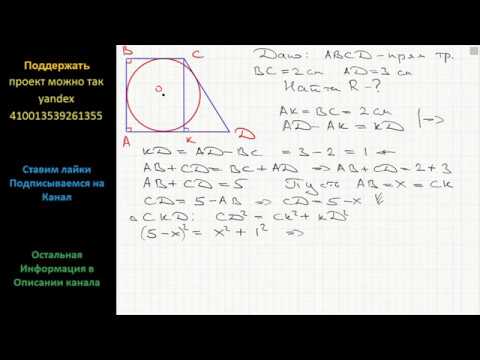 В прямоугольно трапеции один из углов равен 60 градусам, а большая боковая сторона равна 8 см?В прямоугольно трапеции один из углов равен 60 градусам, а большая боковая сторона равна 8 см. Найти основание трапеции и радиус вписанной в нее окружности. Видео:Геометрия В прямоугольную трапецию вписана окружность. Точка касания делит большую боковую сторонуСкачать  Центр вписанной в равнобедренную трапецию окружности отдален от одной из его вершин на 6 см?Центр вписанной в равнобедренную трапецию окружности отдален от одной из его вершин на 6 см. Найдите периметр трапеции если точка касания окружности делит боковую сторону трапеции в отношении 9 и 16. Видео:Геометрия В равнобокую трапеция вписана окружность Одна из ее боковых сторон точкой касания делитсяСкачать  Точка касания окружности, вписанной в прямоугольную трапецию, делит большую боковую сторону на отрезки длинной 3 см и 12 см?Точка касания окружности, вписанной в прямоугольную трапецию, делит большую боковую сторону на отрезки длинной 3 см и 12 см. Найдите площадь трапеции. Видео:Геометрия В прямоугольную трапецию вписана окружность радиуса 12 см Большая из боковых сторон точкойСкачать  Расстояние от центра вписанной в прямоугольную трапецию окружности до концов большей боковой стороны, равны 6 и 8?Расстояние от центра вписанной в прямоугольную трапецию окружности до концов большей боковой стороны, равны 6 и 8. Найти площадь трапеции. Видео:Геометрия В прямоугольную трапецию вписана окружность. Точка касания делит большую боковую сторонуСкачать  Помогите пожалуйстаВ прямоугольную трапецию вписана окружность?В прямоугольную трапецию вписана окружность. Большая боковая сторона точкой касания делится на отрезки 9см и 16см. Найти площадь трапеции. Видео:ЕГЭ ВПИСАННАЯ ОКРУЖНОСТЬ В ПРЯМОУГОЛЬНУЮ ТРАПЕЦИЮ | ЗАДНИЙ ХОД В МАТЕМАТИКЕ ИЛИ КАКОЙ ТО ПОДВОХ |Скачать  Центр окружности описанной около трапеции лежит на ее большем основании?Центр окружности описанной около трапеции лежит на ее большем основании. Боковая сторона трапеции равна 15 радиус окружности 12. 5. найдите площадь трапеции. Видео:Геометрия Точка касания окружности, вписанной в прямоугольную трапецию, делит ее меньшее основаниеСкачать  Одно из оснований равнобедеренной трапеции равно 4?Одно из оснований равнобедеренной трапеции равно 4. Найдите расстояние между точками касания с её боковыми сторонами вписанной в трапецию окружности радиуса 4. Видео:ОГЭ. Математика. Задание 26 | Прямоугольная трапеция и окружность | Борис Трушин |Скачать  Расстояние от центра вписанной в прямоугольную трапецию окружности до концов большой боковой стороны равны 6 см и 8 см?Расстояние от центра вписанной в прямоугольную трапецию окружности до концов большой боковой стороны равны 6 см и 8 см. Найдите площадь трапеции. Видео:Геометрия Равнобокая трапеция вписана в окружность, центр которой принадлежит одному из основанияСкачать  Окружность вписанная в прямоугольную трапецию , делит точкой касания большую боковую сторону на отрезки длиной 25 и 36 см ?Окружность вписанная в прямоугольную трапецию , делит точкой касания большую боковую сторону на отрезки длиной 25 и 36 см . Найдите радиус окружности. Видео:Задача про трапецию, описанную около окружностиСкачать  В прямоугольной трапеции точка касания вписанной окружности делит большую боковую сторону на отрезки 9 см 16 см?В прямоугольной трапеции точка касания вписанной окружности делит большую боковую сторону на отрезки 9 см 16 см. Найдите площадь трапеции. Если вам необходимо получить ответ на вопрос Одна окружность вписана в прямоугольную трапецию, а вторая касается большей боковой стороны и продолжений оснований 1)Доказать, что расстояние между центрами окружностей равно большей боковой стороне ?, относящийся к уровню подготовки учащихся 5 — 9 классов, вы открыли нужную страницу. В категории Геометрия вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы. Видео:Геометрия Точка касания окружности, вписанной в прямоугольную трапецию, делит ее большее основаниеСкачать  Одна окружность вписана в прямоугольную трапецию втораяБАЗА ЗАДАНИЙ Задание № 16. Планиметрия с доказательством. 57. Одна окружность вписана в прямоугольную трапецию, а вторая касается большей боковой стороны и продолжений оснований. а) Докажите, что расстояние между центрами окружностей равно большей боковой стороне трапеции. 58. В остроугольном треугольнике ABC проведены высоты AK и CM. На них из точек M и K опущены перпендикуляры ME и KH соответственно. 59. Точка М – середина гипотенузы АВ треугольника АВС. Серединный перпендикуляр к гипотенузе пересекает катет ВС в точке N. а) Докажите, что ∠ CAN = ∠ CMN 60. В равнобедренной трапеции ABCD основание AD в два раза больше основания BC. 61. В трапеции ABCD основание AD в два раза больше основания BC. Внутри трапеции взяли точку M так, что углы ABM и DCM прямые. 62. Около остроугольного треугольника ABC описана окружность с центром O. На продолжении отрезка AO за точку O отмечена точка K так, что ∠BAC +∠AKC=90°. а) Докажите, что четырёхугольник OBKC вписанный. б) Найдите радиус окружности, описанной около четырёхугольника OBKC, если cos ∠BAC=3/5, а BC=48. 63. В равнобедренной трапеции ABCD основание AD в три раза больше основания BC. 64. В трапеции ABCD боковая сторона AB перпендикулярна основаниям. Из точки A на сторону CD опустили перпендикуляр AH. На стороне AB отмечена точка E так, что прямые CD и CE перпендикулярны. 65. В треугольнике ABC угол ABC тупой, H — точка пересечения продолжений высот, угол AHC равен 60°. 66. В трапеции ABCD с основаниями ВС и AD углы ABD и ACD прямые. 67. Точка Е — середина стороны BС квадрата АВСD. Серединные перпендикуляры к отрезкам АЕ и ЕС пересекаются в точке O. 68. Точка O — центр окружности, описанной около остроугольного треугольника ABC, а BH — высота этого треугольника. 69. В выпуклом четырёхугольнике ABCD известны стороны и диагональ: AB = 3, BC = CD = 5, AD = 8, AC = 7. 70. Четырёхугольник ABCD вписан в окружность радиуса R = 8. Известно, что AB=BC=CD=12. 71. Окружность с центром О 1 касается оснований ВС и AD и боковой стороны АВ трапеции ABCD. Окружность с центром O 2 касается сторон ВС, CD и AD. Известно, что АВ = 10, ВС = 9, CD = 30, AD = 39. 72. Окружность с центром в точке O высекает на всех сторонах трапеции ABCD равные хорды. б) Найдите высоту трапеции, если окружность пересекает боковую сторону AB в точках K и L так, что AK = 11, KL = 10, LB = 4. 73. Окружность проходит через вершины A, B и D параллелограмма ABCD, пересекает сторону BC в точках B и E и пересекает сторону CD в точках K и D. 74. Высоты тупоугольного треугольника АВС с тупым углом АВС пересекаются в точке Н. Угол АНС равен 60 градусов. 75. В трапецию ABCD c основаниями ВС и AD вписана окружность с центром О, СН – высота трапеции, Е – точка пересечения диагоналей. 76. Серединный перпендикуляр к стороне АВ треугольника АВС пересекает сторону АС в точке D. Окружность с центром О, вписанная в треугольник ADB, касается отрезка AD в точке Р, а прямая ОР пересекает сторону АВ в точке К. а) Докажите, что около четырехугольника ВDОК можно описать окружность. б) Найдите радиус этой окружности, если АВ = 10, АС = 8, ВС = 6. 77. Окружность, вписанная в треугольник ABC, касается сторон BC и AC в точках M и N соответственно, E и F — середины сторон AB соответственно. Прямые MN и EF пересекаются в точке D. а) Докажите, что треугольник DFN равнобедренный. б) Найдите площадь треугольника BED, если AB = 20 и ∠ABC = 60°. 78. Медианы AA 1 , BB 1 , CC 1 треугольника ABC пересекаются в точке M. Известно, что AC = 3MB. а) Докажите, что треугольник ABC прямоугольный. б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 12. 79. Четырёхугольник ABCD вписан в окружность. Диаметр CC 1 перпендикулярен стороне AD и пересекает её в точке M, а диаметр DD 1 перпендикулярен стороне AB и пересекает её в точке N. б) Найдите углы четырёхугольника ABCD, если угол CDB вдвое меньше угла ADB. Ответ: б) 72°, 126°, 108°, 54° 80. В прямоугольном треугольнике ABC с прямым углом C известны стороны AC=12, BC=5. Окружность радиусом 0,5 с центром O на стороне BC проходит через вершину C. Вторая окружность касается катета AC, гипотенузы треугольника, а также внешним образом касается первой окружности. а) Докажите, что радиус второй окружности меньше, чем 1/5 длины катета AC. б) Найдите радиус второй окружности. 81. Окружность с центром O проходит через вершины B и C большей боковой стороны прямоугольной трапеции ABCD и касается боковой стороны AD в точке T. а) Докажите, что угол BOC вдвое больше угла BTC. б) Найдите расстояние от точки T до прямой BC, если основания трапеции AB и CD равны 4 и 9 соответственно. 82. Окружность с центром O, вписанная в треугольник ABC, касается его сторон BC, AB и AC в точках K, L и M соответственно. Прямая KM вторично пересекает в точке P окружность радиуса AM с центром A. а) Докажите, что прямая AP параллельна прямой BC. б) Пусть ∠ABC =90°, AM =3, CM =2, Q— точка пересечения прямых KM и AB, а T—такая точка на отрезке PQ, что ∠OAT= 45°. Найдите QT. 83. На гипотенузе AB и на катетах BC и AC прямоугольного треугольника ABC отмечены точки M, N и K соответственно, причем прямая KN параллельна прямой AB и BM =BN =KN/2. Точка P — середина отрезка KN. а) Докажите, что четырехугольник BCPM — равнобедренная трапеция. б) Найдите площадь треугольника ABC, если BM=1 и ∠BCM=15°. 84. В прямоугольном треугольнике ABC точка M лежит на катете AC, а точка N лежит на продолжении катета BC за точку C, причём CM=BC и CN=AC. Отрезки CP и CQ — биссектрисы треугольников ACB и NCM соответственно. а) Докажите, что CP и СQ перпендикулярны. 85. Дана трапеция ABCD с основаниями BC и AD. Точки M и N являются серединами сторон AB и CD соответственно. Окружность, проходящая через точки B и С, пересекает отрезки BM и CN в точках P и Q (отличных от концов отрезков). а) Докажите, что точки M, N, P и Q лежат на одной окружности. б) Найдите радиус окружности, описанной около треугольника MPQ, если прямая DP перпендикулярна прямой PC, AB= 25, BC = 3, CD = 28, AD = 20. 86. В остроугольном треугольнике ABC, ∠A=60°. Высоты BN и CM треугольника ABC пересекаются в точке H. Точка O — центр окружности, описанной около ∆ABC. а) Докажите, что AH=AO. 87. Точка O — центр вписанной в треугольник ABC окружности. Прямая OB вторично пересекает описанную около этого треугольника окружность в точке P. а) Докажите, что ∠POC=∠PCO. 88. Около остроугольного треугольника ABC с различными сторонами описали окружность с диаметром BN. Высота BH пересекает эту окружность в точке K. а) Докажите, что AN=CK. б) Найдите KN, если ∠BAC=35°, ∠ACB=65°, а радиус окружности = 12. 89. Около ∆ABC описана окружность. Прямая BO, где O — центр вписанной окружности, вторично пересекает описанную окружность в точке P. а) Докажите, что OP=AP. б) Найдите расстояние от точки P до прямой AC, если ∠ABC=120°. а радиус описанной окружности равен 18. 🎬 ВидеоУрок 2. Вписанная окружность в четырехугольник. Диаметр - высотаСкачать  Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать  Задание 16 ОГЭ по математике. Окружность вписана в трапецию.Скачать  Простая, но очень противная задача на окружности из ЕГЭ | Планиметрия 83 | mathus.ru #егэ2024Скачать  Планиметрия 27 | mathus.ru | окружность, касающаяся основания трапеции и вписанной в нее окружностиСкачать  🔴 В прямоугольной трапеции основания ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать  Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать  2121 периметр прямоугольной трапеции описанной около окружности равен 100Скачать  |














