Объясните как через данную точку окружности провести касательную к этой

Вопрос по геометрии:

Объясните как через данную точку окружности провести касательную к этой окружности

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Соединить эту точку с центром окружности — получаем радиус. Проводим через точку окружности прямую, перпендикулярно к этому радиусу. Это будет касательная.

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:Построение касательной к окружностиСкачать

Объясните как через данную точку окружности провести

Видео:Строим касательную к окружности (Задача 3).Скачать

Касательная к окружности

О чем эта статья:

Видео:Построение касательной к окружности.Скачать

Касательная к окружности, секущая и хорда — в чем разница

В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.

Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.

Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).

Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой.

Видео:Как с помощью одной линейки построить касательную к окружности?Скачать

Свойства касательной к окружности

Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.

Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.

Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:

• окружность с центральной точкой А;
• прямая а — касательная к ней;
• радиус АВ, проведенный к касательной.

Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.

Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.

В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.

Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Задача

У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.

Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.

Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.

∠АОС = 180° — ∠САО — ∠АСО = 180° — 90° — 28° = 62°

Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, АВ = 62°.

Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.

Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.

Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°.

Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны.

Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.

Задача 1

У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.

Решение

Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.

∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).

Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:

∠BDC = ∠BDA × 2 = 30° × 2 = 60°

Итак, угол между касательными составляет 60°.

Задача 2

К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК.

Решение

Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.

Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.

∠МNК = (180° — ∠МКN) : 2 = (180° — 50°) : 2 = 65°

Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.

Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.

Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.

Задача 1

Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.

Решение

Исходя из соотношения касательной и секущей МА 2 = МВ × МС.

Найдем длину внешней части секущей:

МС = МВ — ВС = 16 — 12 = 4 (см)

МА 2 = МВ × МС = 16 х 4 = 64

Задача 2

Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.

Решение

Допустим, что МО = у, а радиус окружности обозначим как R.

В таком случае МВ = у + R, а МС = у – R.

Поскольку МВ = 2 МА, значит:

МА = МВ : 2 = (у + R) : 2

Согласно теореме о касательной и секущей, МА 2 = МВ × МС.

(у + R) 2 : 4 = (у + R) × (у — R)

Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:

Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).

Ответ: MO = 10 см.

Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.

Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.

Задача 1

Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.

Решение

Согласно свойствам угла между касательной и хордой, ∠АВС = ½ АВ.

АВ = ∠АВС × 2 = 32° × 2 = 64°

Задача 2

У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.

Решение

Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:

КМ = 2 ∠МКВ = 2 х 84° = 168°

Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.

∠ОКМ = ∠ОМК = (180° — ∠КОМ) : 2

Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:

∠ОМК = (180° — ∠КОМ) : 2 = (180° — 168°) : 2 = 6°

Видео:8 класс, 32 урок, Касательная к окружностиСкачать

Объясните как через данную точку окружности провести

Вопрос по геометрии:

Объясните как через данную точку окружности провести касательную к этой окружности

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Соединить эту точку с центром окружности — получаем радиус. Проводим через точку окружности прямую, перпендикулярно к этому радиусу. Это будет касательная.

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Объясните как через данную точку окружности провести касательную к этой окружности?

Геометрия | 5 — 9 классы

Объясните как через данную точку окружности провести касательную к этой окружности.

Соединить эту точку с центром окружности — получаем радиус.

Проводим через точку окружности прямую, перпендикулярно к этому радиусу.

Это будет касательная.

Видео:Касательные к окружностиСкачать

Из данной точки проведены к окружности две взаимно перпендикулярные касательные?

Из данной точки проведены к окружности две взаимно перпендикулярные касательные.

Радиус окружности равен 10 см.

Найдити длин касательных (расстояние от данной точки до точек касания).

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Сколько различных можно провести к окружности через данную точку, лежащую 1) вне окружности : 2)на окружности 3) внутри окружности?

Сколько различных можно провести к окружности через данную точку, лежащую 1) вне окружности : 2)на окружности 3) внутри окружности?

2 ая задача может ли окружность касаться прямой в двух точках помогите пожалуйста.

Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Верно ли что через любую точку вне окружности можно провести к ней только одну касательную?

Верно ли что через любую точку вне окружности можно провести к ней только одну касательную?

Видео:Построение окружности по трём точкам.Скачать

Дана окружность с центром О, ОВ — радиус?

Дана окружность с центром О, ОВ — радиус.

Через точку В к окружности проведена касательная.

Точка С — точка, лежащая на касательной.

Докажите, что отрезок ОС больше радиуса окружности.

Видео:Урок по теме КАСАТЕЛЬНАЯ К ОКРУЖНОСТИСкачать

Дана окружность с центром в точке O?

Дана окружность с центром в точке O.

Через точку A, расположенную вне окружности, и точку O проведена прямая, пересекающая окружность в точках P и Q.

Найдите длину касательной AB, проведенной к данной окружность, если AP = 4, AQ = 9.

Видео:Доказательство того, что радиус перпендикулярен касательной | Окружность | ГеометрияСкачать

Построить окружность с радиусом в 3 сантиметра и отметить точку D удалённую от центра на 5 см и провести через неёё касательную к окружности?

Построить окружность с радиусом в 3 сантиметра и отметить точку D удалённую от центра на 5 см и провести через неёё касательную к окружности.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Из внешней точки к окружности проведены две касательные и в фигуру , ограниченную дугой окружности и касательными, вписана вторая окружность?

Из внешней точки к окружности проведены две касательные и в фигуру , ограниченную дугой окружности и касательными, вписана вторая окружность.

Расстояния от данной точки до центров окружностей равны 6 и 18.

Найдите радиусы окружностей.

Видео:1 2 4 сопряжение окружностейСкачать

Сколько касательных можно провести к окружности через точку : 1)лежащую на окружности 2)лежащую внутри окружности 3)лежащую вне окружности?

Сколько касательных можно провести к окружности через точку : 1)лежащую на окружности 2)лежащую внутри окружности 3)лежащую вне окружности.

Видео:#59. Олимпиадная задача о касательной к окружности!Скачать

Возьмем окружность и точку A вне нее?

Возьмем окружность и точку A вне нее.

Из этой точки к окружности можно провести две касательные.

Пусть одна касается окружности в точке B, а другая в точке C.

Имеет место равенство AB = AC.

Видео:Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

Через точку, данную внутри окружности надо провести хорду так, чтобы она в точке делилась пополам?

Через точку, данную внутри окружности надо провести хорду так, чтобы она в точке делилась пополам.

На этой странице сайта размещен вопрос Объясните как через данную точку окружности провести касательную к этой окружности? из категории Геометрия с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 5 — 9 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.

7)4a² / a = 4a в выражение (a² — 9b²) / 4a = 1 / (4a + 12b) подставим а и б. Смотри ответ на фото. 13поуа не знаю, скину, как решу.

3)6 6)1 : 3 5)x = 2. 5 y = 4. 375.

AOD = 40 угол BOC равен 140 градусов BOC = 180 — 40 = 140 Угол ВОС суміжний с углом AOD Я из Украины поетому не знаю как переводиться суміжні если что преведи.

1) т. К. треугольник ABC — равнобедренный, где AB = BC, то угол A = углу C = 64 градуса, значит по теореме о сумме углов треугольника : Угол B = 180 — (64 + 64) = 52 градуса. 2) Рассмотрим треугольник ABD : Угол B мы нашли, он равен 52 градусам. У..

Значит А = 20 т. К сумма 2 — ух сторон равна 90 т. Е 90 — 70 = 20 а угол А = углу D вот и все.

Объём шара = 4 / 3 Пи * радиус в третьей степени об шара с рад 8 = 4 / 3 * пи * 512 об шара с рад 10 = 4 / 3 * пи * 1000 нужный объём резины = 4 / 3 * пи * 1000 — 4 / 3 * пи * 512 = 4 / 3 * пи (1000 — 512) = 4 / 3 * пи * 488 = примерно 2023 кубически..

Точка пересечения диагоналей параллелограмма делит эти диаонали пополам. Значит, AO = 14 : 2 = 7 ; BO = 10 : 2 = 5. Периметр треугольника AOB = AB + BO + AO. По условию периметр AOB = 20. Значит, AB = 20 — 7 — 5 = 8. Ответ : 8 см.

Троянский вирус это — Вирус который крадёт твои данные, номера телефонов, логины пароли от всего и вся если найдёт и передаёт их создателю вируса.

Если О — это точка пересечения диагоналей, тогда : ∠AOD = 90° [диагонали ромба перпендикулярны] ∠DAO = 160 / 2 = 80° [диагонали ромба — биссектрисы его углов] ∠ADO = 180 — 90 — 80 = 10° [сумма углов треугольника = 180°].

Видео:7 класс, 21 урок, ОкружностьСкачать

Окружность. Касательная к окружности.

Прямая (MN), имеющая с окружностью только одну общую точку (A), называется касательной к окружности.

Общая точка называется в этом случае точкой касания.

Возможность существования касательной, и притом проведенной через любую точку окружности, как точку касания, доказывается следующей теоремой.

Теорема.

Если прямая перпендикулярна к радиусу в его конце, лежащем на окружности, то эта прямая — касательная.

Пусть O — центр некоторого круга и OA какой-нибудь его радиус. Через его конец A проведем MN ⊥ OA.Требуется доказать, что прямая MN — касательная, т.е. что эта прямая имеет с окружностью только одну общую точку A.

Допустим противное: пусть MN имеет с окружностью еще другую общую точку, например B. Тогда прямая OB была бы радиусом и, следовательно, равнялась бы OA.

Но этого быть не может, так как, если OA — перпендикуляр, то OB должна быть наклонной к MN, а наклонная больше перпендикуляра.

Обратная теорема.

Если прямая касательная к окружности, то радиус, проведенный в точку касания, перпендикулярен к ней.

Следствие.

Через всякую данную на окружности точку можно провести касательную к этой окружности и притом только одну, так как через эту точку можно провести перпендикуляр, и притом только один, к радиусу, проведенному в нее.

Теорема.

Касательная параллельная хорде, делит в точке касания дугу, стягиваемую хордой, пополам.

Пусть прямая AB касается окружности в точке M и параллельна хорде СD. Требуется доказать, что ∪CM= ∪MD.

Проведя через точку касания диаметр ME, получаем: EM ⊥ AB и следовательно, EM ⊥ СD. Поэтому СM=MD.

Через данную точку провести касательную к данной окружности.

Если данная точка находится на окружности, то проводят через нее радиус и через конец радиуса перпендикулярную прямую. Эта прямая будет искомой касательной.

Рассмотрим тот случай, когда точка дана вне круга.

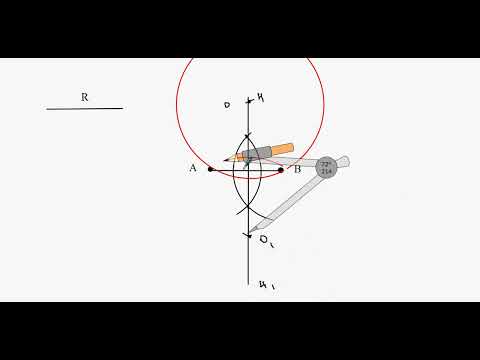
Пусть требуется провести к окружности с центром O касательную через точку A. Для этого из точки A, как из центра, описываем дугу радиусом AO, а из точки O, как центра, пересекаем эту дугу в точках B и С раствором циркуля, равным диаметру данного круга.

Проведя затем хорды OB и OС, соединим точку A с точками D и E, в которых эти хорды пересекаются с данной окружностью. Прямые AD и AE — касательные к окружности O. Действительно, из построения видно, что треугольники AOB и AOС равнобедренные (AO = AB =AС) с основаниями OB и OС, равными диаметру круга O.

Так как OD и OE — радиусы, то D — середина OB, а E — середина OС, значит AD и AE — медианы, проведенные к основаниям равнобедренных треугольников, и потому перпендикулярны к этим основаниям. Если же прямые DA и EA перпендикулярны к радиусам OD и OE, то они — касательные.

Следствие.

Две касательные, проведенные из одной точки к окружности, равны и образуют равные углы с прямой, соединяющей эту точку с центром.

Так AD=AE и ∠OAD = ∠OAE потому, что прямоугольные треугольники AOD и AOE, имеющие общую гипотенузу AO и равные катеты OD и OE (как радиусы), равны. Заметим, что здесь под словом “касательная” подразумевается собственно “отрезок касательной” от данной точки до точки касания.

🎦 Видео

10 класс, 3 урок, Некоторые следствия из аксиомСкачать

Построение касательных | Задачи 1-10 | Решение задач | Волчкевич | Уроки геометрии 7-8 классСкачать

Окружность данного радиуса, проходящей через две заданные точкиСкачать