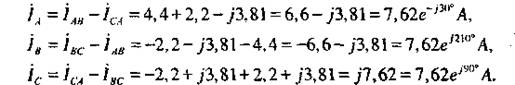Обрыв линейного провода треугольник (4 видео)

Режим обрыва линейного провода

Дата добавления: 2015-08-31 ; просмотров: 13513 ; Нарушение авторских прав

Рассмотрим, как изменится режим работы фаз приёмника, соединённого по схеме треугольник, если произойдёт обрыв одного из линейных проводов (допустим линейного провода B-b). Нагрузка до обрыва была симметричной.

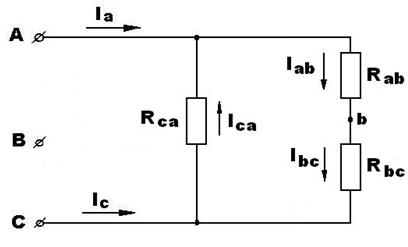
Электрическая схема при обрыве линейного провода B-b будет иметь следующий вид (рис. 49).

После обрыва линейного провода трёхфазная цепь по схеме треугольник преобразуется в однофазную цепь с двумя параллельными ветвями, включённую на линейное напряжение .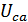

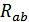
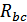
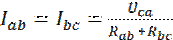
По фазам с сопротивлениями и будет протекать один и тот же ток равный:

. (4.9)

Ток в фазе СА не изменится и будет равен:

. (4.10)

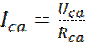
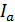
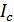
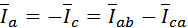
Линейные токи и будут равны по величине, но противоположны по направлению:

. (11)

Рисунок 49. Электрическая схема после обрыва

линейного провода B-b

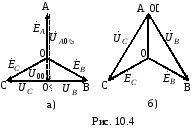
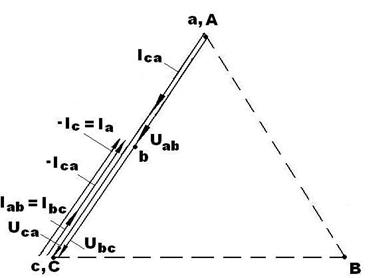
Согласно уравнениям (4.9) – (4.11) на рис. 50 изображена векторная диаграмма токов и напряжений при обрыве линейного провода B-b.

Рисунок 50. Векторная диаграмма токов и напряжений

при обрыве линейного провода B-b

Исходя из вышесказанного, можно сделать следующие выводы:

1. Напряжение на фазах, соединённых с оборванным линейным проводом, уменьшается. Если нагрузка первоначально была симметричной, эти напряжения будут равны половине линейного напряжения:

U_ab=U_bc= .

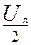
2. Напряжение на третьей фазе остаётся неизменным и равным линейному напряжению:

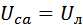
3. Токи в фазах, соединённых с оборванным линейным проводом, уменьшаются.

4. Ток в третьей фазе остаётся неизменным.

\|	следующая лекция ==>
\|

Не нашли то, что искали? Google вам в помощь!

Содержание

ДОМОСТРОЙСантехника и строительство
Аварийные режимы в нагрузках соединенных звездой
Аварийные режимы в нагрузках соединенных треугольником
25. Как изменятся линейные токи при обрыве фазного провода?
26. Как изменятся фазные токи при обрыве линейного провода?
27. Как изменятся линейные токи при обрыве линейного провода?
Трехфазные цепи при соединении треугольником
📺 Видео

Видео:#001."Звезда" или "Треугольник"?Скачать

ДОМОСТРОЙСантехника и строительство

Четверг, 12 декабря 2019 1:08
Автор: Sereg985
Прокоментировать

Рубрика: Строительство
Ссылка на пост
https://firmmy.ru/

Для соединения трехфазной цепи в звезду возможны следующие аварийные режимы работы:

1) обрыв фазы (рис. 3.10);

2) обрыв нулевого провода (рис. 3.11);

3) короткое замыкание фазы при обрыве нуля (рис. 3.12).

4) обрыв фазы и нуля, рис. 3.12.

Для соединения трехфазной цепи в треугольник возможны следующие аварийные режимы:

2) обрыв линейного провода.

Аварийные режимы в нагрузках соединенных звездой

1) При обрыве фазы А , работа нагрузкой не совершается, а остальные нагрузки () свои режимы работы не изменят (рис. 3.13): .

Если нагрузки связаны и является одним целым, то этот режим будет аварийным. Так, если эта нагрузка – асинхронный двигатель, то он будет в аварийном режиме и нулевой провод будет нагружен дополнительно (рис. 3.13):

2) Обрыв нулевого провода не всегда вызывает аварию в трехфазных цепях. Если нагрузка симметрична, то обрыв нулевого провода не изменит токов нагрузок, так как для симметричной нагрузки

Для несимметричных нагрузок , и поэтому такой режим может вызвать аварию.

Для того чтобы показать это, используем метод двух узлов:

Напряжение (рис. 3.14) не равно нулю, если нагрузки несимметричны. Фазные токи также будут неодинаковыми.

3) При коротком замыкании фазы А и обрыве нуля напряжение этой фазы равно нулю:, (рис. 3.15).

Нагрузка фазы В увеличится в раз:

Аналогично и в фазе С:

;

будет увеличен по отношению к исходному в раз.

4) Обрыв фазы и нулевого провода дает:

В оставшихся фазах токи будут одинаковыми, а напряжения на них будут зависеть от сопротивлений нагрузок (рис. 3.16).

Аварийные режимы в нагрузках соединенных треугольником

1) Обрыв фазы.

Ключ к1 замкнут, ключ к2 разомкнут (рис. 3.17). В этом режиме ток в фазе отсутствует, а остальные нагрузки работают как обычно (рис. 3.18). В таком аварийном режиме линейные токи фаз А и В соответствуют фазным токам, а линейный ток фазы С остается таким, каким был прежде.

Обрыв линейного провода. Ключ к1 разомкнут и ключ к2 замкнут (рис. 3.19). Фаза нагрузки с своего режима не изменит, а фазы становятся последовательно соединенными и параллельно подключеннымик линейному напряжению фаз В, С (см. рис. 3.17), то есть цепь становитсяоднофазной. Топографическая и векторная диаграммы в этом случае могут иметьвид, как показано на рис.3.19.

Звезда-звезда без нейтрального провода..

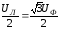
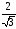
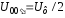
Обрыв фазного провода (например, фазы А). В этом режиме нагрузки Z_B и Z_C в двух других фазах оказываются включенными последовательно под линейное напряжение. Напряжение на нагрузках (при их равенстве) станет и, следовательно, уменьшится враз. При этом появится смещение нейтрали (напряжение между нулевыми точками генератора и нагрузки), равное(рис. 10.4,а). В месте разрыва напряжение U_AO’ возрастет в 1,5 раза и станет равным 1,5U_ф (рис. 10.4, а).

Звезда-звезда с нейтральным проводом. Обрыв фазного провода (например, фазы А). В этом режиме напряжения на нагрузках, включенных в другие фазы, не изменятся, но появится ток в нейтральном проводе.

Нагрузка включена треугольником. В этой схеме возможны обрыв фазного, линейного проводов и короткое замыкание нагрузки.

Обрыв фазного провода (Z_ab=). В этом режиме токи и напряжения в других фазах нагрузки не изменяются, а линейные токи I_a и I_b станут равны фазным токам, т.е. уменьшатся в 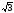раза. Линейный токI_c не изменится (рис. 10.5, а)

Видео:Несимметричная нагрузка. Схема соединения "треугольник"Скачать

25. Как изменятся линейные токи при обрыве фазного провода?

Видео:Соединение обмоток треугольникомСкачать

26. Как изменятся фазные токи при обрыве линейного провода?

Обрыв линейного провода (например, А). В этом режиме ток и напряжение на нагрузке Z_bc не изменится, а на нагрузках Z_ab и Z_ca уменьшатся в 2 раза, так как они оказываются включенными последовательно под то же напряжение U_BC (рис. 10.5, в). Линейные токи I_B и I_C будут равны 1,5I_ф и, следовательно, уменьшатся по сравнению с исходным симметричным режимом, когда они были равны 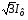(рис. 10.5,в).

Видео:Обрыв Фазы. Расчет трехфазной цепи - Звезда без нейтрального проводаСкачать

27. Как изменятся линейные токи при обрыве линейного провода?

Как изменятся токи в фазах приемника при обрыве линейного провода А. [1]

Построить векторную диаграмму напряжений и токов при обрыве линейного провода трехфазной сети и привести соображения о влиянии этого вида повреждения на режим работы отдельных приемников. [2]

Как изменятся токи или напряжения в цепи при обрыве линейного провода или коротком замыкании фазы. Подобные режимы возникают при неисправностях в приемниках энергии, перегорании предохранителя и других аномалиях в цепи. [3]

Из схемы рис. 4.26 видно, что при обрыве линейного провода А фазы ab и са окажутся соединенными последовательно и, следовательно, их общее сопротивление возрастет вдвое. [4]

Таким образом, и в случае соединения треугольником при обрыве линейного провода мощность потребителя уменьшается вдвое. [5]

Осветительная сеть.| Частные случаи несимметричной нагрузки.

Из диаграммы видно, что система трехфазного переменного тока при обрыве линейного провода превратилась в однофазную. [6]

При наличии нейтрального провода для электроприемников, приключенных к неповрежденным линейным проводам, обрыв чужого линейного провода практически не ощущается. При отсутствии нейтрального провода фазные напряжения на зажимах обоих последовательно соединенных электроприемников пропорциональны величинам их полных сопротивлений. Преобладание в одной из этих фаз индуктивной нагрузки, а в другой — емкостной нагрузки может привести к резонансу напряжений с установлением значительных перенапряжений на зажимах электроприемников и к резкому увеличению потребляемого тока. [7]

Стационарный пульт ЦПА-П позволяет производить опробование тормозов и выявлять основные неисправности электропневматических тормозов: обрыв линейного провода или его отводов, неисправность электровоздухораспределителей и межвагонных соединений, к

При обрыве одной фазы граничные условия (рис. 9.2) таковы:

Условие (9.4), выраженное через симметричные составляющие тока особой фазы, имеет вид:

Рис. 9.2. Обрыв олной фазы

Падение напряжения прямой последовательности между точками I и и оборванной фазы

или, с учетом (9.5) и (9.6),

Аналогичные расчеты для а0_1А2 и Д 1/₁₀ дают: и

В соответствии с (9.8) можно приравнять правые части уравнений (9.2) и (9.3):

Подстановка этого выражения в (9.7) дает: откуда

Если подставить последнее выражение в (9.9), то получим:

Чтобы получить искомое расчетное выражение для тока прямой последовательности ,, следует в соответствии с (9.8) приравнять правые части уравнений (9.1) и (9.2) и в полученном равенстве ток 1_1Л2 выразить через 1_1Л , используя выражение (9.10):

где верхний индекс (1) обозначает обрыв одной фазы.

Последнее выражение показывает, что для определения тока прямой последовательности при обрыве одной фазы следует в каждую фазу в месте обрыва (т.е. между точками I и Ь’) включить дополнительный элемент с одинаковым сопротивлением АХ Читайте также Легкий пирог с малиной рецепт

обрыва для особой фазы , е0_1Л2 и АО₁₀, определить симметричные составляющие напряжения этой фазы с другой стороны обрыва. При этом удобно пользоваться эпюрами распределения напряжений прямой, обратной и нулевой последовательностей, показанными на рис. 9.4, г (эпюр распределения напряжения нулевой пос-

Рис. 9.4. Схемы замещения прямой (о), обратной (и) и нулевой («) последовательностей и эпюры распределения симметричных составляющих напряжения особой фаты (с)

ледовательности условно показан короче других, так как обычно схема замещения нулевой последовательности содержит меньше элементов, чем схемы замещения прямой и обратной последовательностей). Как видно из рис. 9.4, г, при переходе от точки Ь к точке или от и к Ь составляющие напряжений обратной и нулевой последовательностей особой фазы изменяют знак на противоположный (со стороны большей ЭДС они положительны, а со стороны меньшей ЭДС отрицательны). Полученные указанным способом векторные диаграммы напряжений в точках Ь и Ь’ представлены на рис. 9.5. Из этих диаграмм и формулы (9.8) видно, что при переходе от точки I к точке

напряжение оборванной фазы 11₁₄ уменьшается на Д (] _1А —

= 3 а0_1лх, а напряжения неповрежденных фаз О_1В и _1С остаются неизменными.

Комплексную схему замещения, в которой выполнялись бы все соотношения для симметричных составляющих токов и падения напряжения, характерных при обрыве одной фазы, получить путем

Рис. 9.5. Векторные диаграммы напряжении в точках Ца) и L’ (б)

непосредственного соединения схем замещения разных последовательностей невозможно, так как потенциалы в точках . I, и 1 , а

, и L’ , как видно из эпюр распределения напряжений (рис. 9.4, г), неодинаковы. Чтобы обеспечить выполнение соотношений (9.7) и (9.8) и не смещать потенциалы в схемах обратной и нулевой последовательностей, необходимо схемы замещения разных последовательностей связать по месту обрыва фазы с помощью идеальных трансформаторов с коэффициентом трансформации п = 1/1, как показано на рис. 9.6. Связывающая часть схемы, включающая вторичные обмотки идеальных трансформаторов, обеспечивает равенство симметричных составляющих падения напряжения в месте обрыва и равенство нулю суммы симметричных составляющих тока оборванной фазы.

Более широкое применение, однако, находит упрощенная комплексная схема замещения, которая представлена на рис. 9.7. Она получена непосредственным соединением между собой точек ?₂

и ?₍₎, а также точек L, L’₂ и L’_q . При этом потенциалы во всех точках

схем замещения обратной и нулевой последовательностей, в том числе и в началах схем, оказываются смещенными, поэтому такая комплексная схема замещения справедлива только для симметричных составляющих токов.

Рис. 9.6. Комплексная схема замещения при обрыве одной фазы

Рис. 9.7. Упрощенная комплексная схема замещения при обрыве одной фазы

Видео:Трехфазные цепи. Схема соединения "ЗВЕЗДА"Скачать

Трехфазные цепи при соединении треугольником

Особенности включения трехфазных систем треугольником. При соединении трехфазных систем треугольником также используются три гармонических напряжения (4.1), которые были рассмотрены в лекции 15. Однако соединение этих источников выполняется таким образом, что начало одной фазы соединяется с концом другой. На рис. 4.5а показано такое включение трех обмоток генератора и соответствующее ему включение источников напряжения .

Векторная диаграмма для, соединения обмоток генератора по схеме треугольника приведена на рис. 4.5, б. На этой диаграмме полагается, что вектора напряжений генератора имеют значения

(4.1)

т. е. генератор считается симметричным с прямым чередованием фаз.

При соединении нагрузок треугольником фазные напряжения будут равны линейным, а линейные токи равны геометрической разности двух фазных токов, подходящих к вершине треугольника нагрузок, как показано на рис. 4.6. При этом для положительных направлений токов справедливы следующие соотношения, которые устанавливают связь между линейными и фазными токами

(4.2)

Фазные токи рассчитываются по известным линейным напряжениям и проводимостям Y_AB, Y_BC, Y_CA фаз приемников

(4.3)

Если падения напряжений на проводах линий передачи малы, то можно считать, что напряжения генератора равны соответствующим напряжениям приемника, т. е. .

Из уравнений (26.2) также следует, что при любых значениях фазных токов для линейных токов справедливо выражение

(4.4)

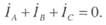
Следует отметить, что включение нагрузок по схеме треугольника возможно при любом включении обмоток генератора, как по схеме треугольника, так и по схеме звезды. Однако, при включении генератора по схеме звезды фазные напряжения приемника будут равны линейным напряжениям генератора. При этом нулевая точка генератора не используется.

Рассмотрим некоторые частные режимы работы при включении нагрузок по схеме треугольника. К таким режимам относятся:

□ равномерная нагрузка фаз генератора;

□ неравномерная нагрузка фаз генератора;

□ обрыв одной фазы приемника;

□ обрыв двух фаз приемника;

□ обрыв линейного провода.

Короткое замыкание любой фазы приемника приводит к аварийному режиму, так как при этом замыкается накоротко одна из обмоток генератора, и поэтому недопустимо.

Равномерная нагрузка фаз генератора.При симметричной системе напряжений генератора, определяемых уравнениями (4.1) и одинаковой нагрузке фаз приемника (Y_AB = Y_BC = Y_CA = Y_n) действующие значения токов в фазах равны между собой, поэтому линейные токи связаны с фазными токами соотношением

(4.5)

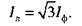
Токи в фазах приемника определяются по формулам (4.3) и при равенстве проводимостей имеют значения

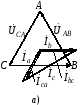
Векторная диаграмма для равномерной нагрузки фаз генератора приведена на рис. 4.7а.

Неравномерная нагрузка фаз генератора.Неравномерная нагрузка фаз генератора является наиболее распространенным режимом работы трехфазной системы. Неравномерная нагрузка характеризуется различными значениями проводимостей, включенных в приемнике, т. е. Y_AB = Y_BC = Y_CA. Действующие значения токов в фазах приемника при неравномерной нагрузке и симметричном генераторе пропорциональны проводимостям нагрузки и определяются по формулам (26.3).

Векторная диаграмма для неравномерной нагрузки фаз генератора приведена на рис. 4.7б. Линейные токи при неравномерной нагрузке фаз можно определить по формулам (4.2).

Обрыв одной фазы приемника. При обрыве одной фазы приемника ток в ней будет равен нулю. Токи в других фазах приемника не изменятся, так как не изменятся фазные напряжения.

В линейном проводе, не связанном с оборванной фазой, ток также не изменится. Линейные токи двух других фаз станут равными фазным токам.

Например, при обрыве фазы А-В приемника ток I_A_В = 0, а токи других фаз не изменятся. Линейные токи в этом случае будут иметь следующие значения

. (4.7)

Векторная диаграмма обрыва фазы А-В приведена на рис. 4.7, в.

Обрыв двух фаз приемника. При обрыве двух фаз приемника ток в них будет равен нулю. Ток в неповрежденной фазе не изменится, так как напряжение на ней сохранится неизменным.

Ток в линейном проводе, подходящем к оборванным фазам, будет равен нулю. Токи в других линейных проводах станут равны фазным токам.

Так, например, при обрыве фаз А-В и В-С фазные токи I_АВ = I_BC = 0, а линейные токи примут значения

(4.8)

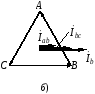
Векторная диаграмма токов и напряжений при обрыве двух фаз приемник приведена на рис. 4.7, г.

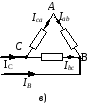
Обрыв линейного провода. При обрыве линейного провода трехфазная система превращается в однофазную. При этом напряжение и ток в фазе, не связанной с оборванным линейным проводом, останутся без изменений.

Две другие фазы, связанные с оборванным линейным проводом, оказываются соединенными последовательно и подключенными параллельно первой фазе.

Так, например, при обрыве линейного провода А фазы А-В и В-С будут включены последовательно и подключены параллельно фазе В-С, напряжение на которой равно U_BC.

Токи в фазах определяются уравнениями

Векторная диаграмма токов и напряжений при обрыве линейного провода приведена на рис. 4.7, д.

Трехфазная система звезда — треугольник. Выше было сказано, что способ соединения обмоток генератора не предопределяет способ соединения нагрузок. Поэтому на практике к трехфазному генератору, включенному по схеме звезды, можно подключить нагрузку, соединенную по схеме треугольника. Схема подобного подключения приведена на рис. 4.8.

Из этой схемы следует, что каждое плечо треугольника оказывается включенным на линейное напряжение генератора; соединенного по схеме звезды. Поскольку линейное напряжение в 3 раза больше фазного, то токи в фазах симметричного приемника также вырастут в 3 раза. В общем случае их можно определить по формулам

(4.9)

При расчете от системы звезда-треугольник можно перейти к системе звезда-звезда. При таком преобразовании можно использовать эквивалентность схем звезды и треугольника, при которой сохраняются все напряжения и токи на внешних зажимах этих схем. Такое преобразование приводит в общем случае к эквивалентным сопротивлениям схемы звезды

(4.10)

Из уравнений (4.10) получим, что для симметричного треугольника с проводимостями Y_Δ можно найти сопротивления эквивалентной звезды

(4.11)

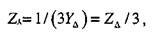
откуда следует, что сопротивления эквивалентной звезды для симметричной схемы в три раза меньше сопротивлений треугольника.

Следует отметить, что хотя в результате такого преобразования получается система звезда-звезда, ввести в нее нулевой провод нельзя, так как в реальной схеме этого соединения нет и при введении нулевого провода получается схема, отличная от исходной.

Пример 2. Требуется определить линейные токи в нагрузке, соединенной треугольником, которая подключена к симметричному трехфазному генератору с линейным напряжением Е_л = 220 В. Сопротивления фаз приемника имеют значения: Z_AB = Z_BC = 50 Ом, Z_CA = (30 + j40) Ом. Схема соединений генератора t нагрузкой приведена на рис. 4.9, а.

Решение. Приемник с такими нагрузками относится к разряду схем с неравномерной нагрузкой фаз генератора. Для определения линейных токов в такой схеме можно воспользоваться уравнениями (4.2), в которые входят фазные токи, определяемые по уравнениям (4.3). В связи с этим, определим вначале фазные токи, пользуясь уравнениями (4.3)