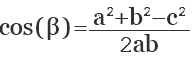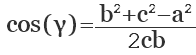В данной статье мы рассмотрим определение и свойства равностороннего (правильного) треугольника. Также разберем пример решения задачи для закрепления теоретического материала.
Видео:№228. Найдите углы равнобедренного треугольника, если один из его углов равен: а) 40°Скачать

Определение равностороннего треугольника
Равносторонним (или правильным) называется треугольник, в котором все стороны имеют одинаковую длину. Т.е. AB = BC = AC.
Примечание: правильный многоугольник – это выпуклый многоугольник, имеющий равные стороны и углы между ними.
Видео:№254. Найдите углы равнобедренного прямоугольного треугольника.Скачать

Свойства равностороннего треугольника
Свойство 1
В равностороннем треугольнике все углы равны 60°. Т.е. α = β = γ = 60°.
Свойство 2
В равностороннем треугольнике высота, проведенная к любой из сторон, одновременно является биссектрисой угла, из которого она проведена, а также медианой и серединным перпендикуляром.
CD – медиана, высота и серединный перпендикуляр к стороне AB, а также биссектриса угла ACB.
Свойство 3
В равностороннем треугольнике биссектрисы, медианы, высоты и серединные перпендикуляры, проведенные ко всем сторонам, пересекаются в одной точке.
Свойство 4
Центры вписанной и описанной вокруг равностороннего треугольника окружностей совпадают и находятся на пересечении медиан, высот, биссектрис и серединных перпендикуляров.
Свойство 5
Радиус описанной вокруг равностороннего треугольника окружности в 2 раза больше радиуса вписанной окружности.
- R – радиус описанной окружности;
- r – радиус вписанной окружности;
- R = 2r.
Свойство 6
В равностороннем треугольнике, зная длину стороны (условно примем ее за “a”), можно вычислить:
1. Высоту/медиану/биссектрису:
2. Радиус вписанной окружности:
3. Радиус описанной окружности:
4. Периметр:
5. Площадь:
Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Пример задачи
Дан равносторонний треугольник, сторона которого равна 7 см. Найдите радиус описанной вокруг и вписанной окружности, а также, высоту фигуры.
Решение
Применим формулы, приведеные выше, для нахождения неизвестных величин:
Видео:Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Углы равностороннего треугольника
Чему равны углы равностороннего треугольника?
(свойство углов равностороннего треугольника)
Все углы равностороннего треугольника равны по 60º.
Аналогично, так как AC=BC, ∠A=∠B.
Отсюда следует, что в равностороннем треугольнике все углы равны между собой: ∠A=∠B=∠C
Так как сумма углов треугольника равна 180º, то ∠A=∠B=∠C=180º:3=60º, то есть каждый угол равностороннего треугольника равен 60º.
Что и требовалось доказать .
Тот факт, что все углы равностороннего треугольника равны между собой, можно рассмотреть также как следствие из теоремы о соотношении между сторонами и углами треугольника. В треугольнике напротив большей стороны лежит больший угол, напротив меньшей стороны — меньший угол. Так как все три стороны правильного треугольника равны, то и все углы тоже равны.
Видео:№225. Докажите, что каждый угол равностороннего треугольника равен 60°.Скачать

Углы треугольника
Геометрическая фигура из трех отрезков, соединенных между собой тремя точками, не лежащими на одной прямой, называется треугольником. Это — многоугольник с тремя углами. Сумма всех углов треугольника равна 180°. Если известна величина двух из них, третий угол определяем вычитанием из 180° величины двух известных углов.
α = 180°-β-γ
Если известны стороны треугольника, можно рассчитать его углы, воспользовавшись теоремой косинусов. Здесь, квадрат одной стороны треугольника (а) равен сумме квадратов двух его других сторон (b,с), образующих искомый угол (α), плюс удвоенное произведение этих сторон (b,с) на косинус угла.
a 2 = b 2 + c 2 + 2abc cos (α)
Отсюда, косинус искомого угла равняется сумме квадратов смежных сторон (b, с) минус квадрат третей стороны треугольника (а), противолежащей искомому углу, и все это делится на удвоенное произведение смежных сторон:
cos (α) = (b 2 + c 2 — a 2 ) / 2bc
,
где а, b, с — стороны треугольника.
Используя теорему косинусов, определяем косинусы остальных углов. Величины углов в градусах находим по тригонометрической таблице.
💥 Видео
Геометрия Равносторонний треугольникСкачать

№227. Найдите углы равнобедренного треугольника, если: а) угол при основании в два разаСкачать

Определение угла равнобедренного треугольникаСкачать
Соотношения между сторонами и углами треугольника. 7 класс.Скачать

Как найти величины углов всех треугольников. Сумма углов треугольника. Геометрия 7 класс.Скачать

Найдите углы прямоугольного треугольника, если его гипотенуза равна 12, а площадь равна 18Скачать

Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Только 1 может решить эту хитрую задачу ★ Найдите углы треугольника ★ Супер ЖЕСТЬСкачать

Равнобедренный треугольник. 7 класс.Скачать

Решение прямоугольных треугольниковСкачать

Свойства равнобедренного треугольника. 7 класс.Скачать

№234. Один из внешних углов равнобедренного треугольника равен 115°. Найдите углы треугольника.Скачать

7 кл г. Теорема: «катет лежавший напротив угла в 30 градусов равен половине гипотенузы»Скачать

№116. Докажите, что в равностороннем треугольнике все углы равны.Скачать

Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать