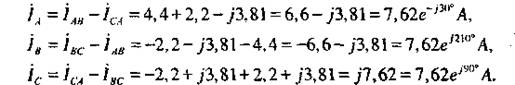а) Назначение нулевого провода.
При несимметричной нагрузке звездой без нулевого провода (на рис. 11.19 ключ разомкнут) сопротивления всех фаз неодинаковы: Z А 

Это напряжение U N, действующее между точками N и N’ (рис. 11.19), показано на рис. 11.20. При любом направлении вектора U N напряжения на фазах нагрузки будут неодинаковы.
При включении и выключении приемников проводимости фаз Y А, Y B и Y C изменяются произвольным образом, это приводит к изменению напряжения смещения нейтрали U N, ведущее, в свою очередь, к произвольному изменению напряжений на фазах нагрузки. Подавляющее большинство электросиловых приемников функционирует только при номинальном питающем напряжении. Поэтому соединение звездой без нулевого провода для несимметричной или изменяемой нагрузки практически не используется вследствие невозможности обеспечить номинальное питающее напряжение. При большом числе приемников, статистически в «среднем» обеспечивающих примерно одинаковую нагрузку фаз, несмотря на включение и выключение отдельных потребителей, смещение нейтрали невелико. Это позволяет использовать соединение звездой без нулевого провода для мощных линий электропередач на трансформаторные подстанции напряжением до 6,3 кВ. Соединение звездой без нулевого провода используется и в устройствах, предназначенных для контроля и анализа режимов трехфазных цепей.
б) Соединение звездой с нулевым проводом.
Для соединения звездой с нулевым проводом (на рис. 11.19 ключ замкнут) определим напряжение нейтрали также по формуле двух узлов:
В реальных системах электроснабжения проводимость нулевого провода Y N много больше проводимостей фаз и практически можно считать, что сопротивление нулевого провода близко к нулю. Тогда при Y N → ∞ знаменатель в выше написанной формуле стремится к бесконечности, U N → 0 и при наличии нулевого провода с достаточно малым сопротивлением смещение потенциала нулевой точки N’ нагрузки отсутствует. На фазах нагрузки независимо от их сопротивлений поддерживаются напряжения, составляющие симметричную трехфазную систему.
Токи фаз нагрузки определяются по закону Ома:

Ток нейтрального провода (см. рис. 11.14) можно определить по первому закону Кирхгофа для узла N’ — рис. 11.22 (на рисунке изображен вспомогательный вектор тока, равный сумме токов I А+ I С):
Чем больше несимметрия фаз нагрузки, тем больше «уравнительный» ток I N нулевого провода.
Соединение звездой с нулевым проводом повсеместно используется для электропитания жилых и общественных зданий, производственных приемников энергии и в других случаях с многочисленными приемниками, включаемыми и выключаемыми независимо друг от друга.

Если пренебречь сопротивлением соединительных проводов, то напряжения на фазах нагрузки равны линейным напряжениям трехфазного источника . Фазные токи при несимметричной нагрузке Z А B 

На рис. 11.25 показана векторная диаграмма токов при несимметричной активной нагрузке. Линейные токи определяются по первому закону Кирхгофа для узлов А, В и С рис. 11.17:
Как видно из векторной диаграммы (рис. 11.25), линейные токи не равны по модулю и смещены по фазе на углы, не равные 120°. В общем случае и фазные токи не равны по модулю и смещены по фазе на углы, не равные 120°.
Векторная диаграмма линейных токов показана на рис. 11.25.
г) Аварийные режимы в трехфазных цепях.
Частными случаями несимметричных режимов являются аварийные режимы в трехфазных цепях: обрывы нейтрального и линейных проводов, КЗ в фазах.
Абсолютно безопасными являются разрывы в фазах нагрузки, соединенной треугольником или звездой с нулевым проводом (отключения фаз)
Аварийными, пожароопасными являются КЗ фаз нагрузки таких соединений. Все другие случаи приводят к резкому изменению номинальных напряжений на фазах нагрузки и могут привести к аварийной ситуации. Обрыв нулевого провода несимметричной звезды был рассмотрен в примере 11.9.
Для соединения трехфазной цепи в звезду возможны следующие аварийные режимы работы:
1) обрыв фазы (рис. 3.10);
2) обрыв нулевого провода (рис. 3.11);
3) короткое замыкание фазы при обрыве нуля (рис. 3.12).
4) обрыв фазы и нуля, рис. 3.12.
Для соединения трехфазной цепи в треугольник возможны следующие аварийные режимы:
2) обрыв линейного провода.
- Аварийные режимы в нагрузках соединенных звездой
- Аварийные режимы в нагрузках соединенных треугольником
- Трехфазные цепи при соединении треугольником
- 3.5. Несимметричные и аварийные режимы работы трехфазных цепей
- Аварийные режимы в нагрузках соединенных звездой
- Аварийные режимы в нагрузках соединенных треугольником
- 📹 Видео
Аварийные режимы в нагрузках соединенных звездой
1) При обрыве фазы А 




2) Обрыв нулевого провода не всегда вызывает аварию в трехфазных цепях. Если нагрузка симметрична, то обрыв нулевого провода не изменит токов нагрузок, так как для симметричной нагрузки

Для несимметричных нагрузок 
Для того чтобы показать это, используем метод двух узлов:


3) При коротком замыкании фазы А и обрыве нуля напряжение этой фазы равно нулю:
Нагрузка фазы В увеличится в 

Аналогично и в фазе С:



4) Обрыв фазы и нулевого провода дает:

В оставшихся фазах токи будут одинаковыми, а напряжения на них будут зависеть от сопротивлений нагрузок (рис. 3.16).
 Аварийные режимы в нагрузках соединенных треугольником
Аварийные режимы в нагрузках соединенных треугольником
1) Обрыв фазы.
Ключ к1 замкнут, ключ к2 разомкнут (рис. 3.17). В этом режиме ток в фазе 
2)
Обрыв линейного провода. Ключ к1 разомкнут и ключ к2 замкнут (рис. 3.19). Фаза нагрузки с 

Общие сведения
При коротких замыканиях в фазах нагрузки или между линейными проводами токи резко возрастают и происходит аварийное отключение установки защитой.
Обрывы фаз или линейных проводов при соединении нагрузки в треугольник не приводят к перегрузкам по токам или напряжениям, как это иногда случается при соединении нагрузки в звезду.
При обрыве одной фазы нагрузки (рис. 8.5.1) ток этой фазы становится равным нулю, а в оставшихся двух фазах ток не меняется. Два линейных тока уменьшаются в 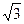
При обрыве линейного провода (например, В) фазные сопротивления RAB и RBC оказываются соединёнными последовательно и включёнными параллельно с сопротивлением RCA на напряжение UCA (рис. 8.5.2). Цепь фактически становится однофазной.

При одновременном обрыве линейного провода и одной фазы нагрузки цепь также становится однофазной (рис. 8.5.3 и 8.5.4).
Экспериментальная часть
Задание
Экспериментально исследовать аварийные режимы трёхфазной цепи при соединении нагрузки в треугольник.
Порядок выполнения работы
· Соберите цепь цепь согласно схеме (рис.8.5.5) с сопротивлениями фаз RAВ=RBС=RCА=1кОм и измерьте линейные и фазные токи в симметричном режиме.
· Проделайте измерения фазных и линейных токов (отличных от нуля) во всех режимах, указанных в табл. 8.5.1. (Измерения токов можно производить одним – двумя амперметрами, переключая их из одной фазы в другую, либо виртуальными приборами).
· По экспериментальным данным постройте векторные диаграммы для каждого аварийного случая в выбранном масштабе.
· Ответьте на контрольные вопросы.
| Режим | IAB, мА | IBC, мА | ICA, мА | IA, мА | IB, мА | IC, мА |
| Симметричный режим, Rф=1 кОм | ||||||
| Обрыв фазы АВнагрузки | ||||||
| Обрыв линейного провода А | ||||||
| Обрыв фазы АВ и линии С | ||||||
| Обрыв фазы АВи линииА |
Векторные диаграммы
- Обрыв фазы АВ нагрузки
Обрыв линейного провода А
3. Обрыв фазы АВ и линии С 4. Обрыв фазы АВ и линии А
Вопрос:Как вычислить мощность несимметричной трёхфазной нагрузки?
Ответ: ……….
Вопрос:Как (во сколько раз) увеличиваются или уменьшаются фазные и линейные токи в каждом из рассмотренных аварийных режимов?
Ответ: ……….
Расчёт и экспериментальное исследование цепи при несинусоидальном приложенном напряжении
(для компьютерного варианта стенда)
Общие сведения
Несинусоидальное периодическое напряжение, приложенное к электрической цепи, можно разложить в ряд Фурье:
Расчёт цепи проводят с использованием принципа наложения в следующей последовательности:
· рассчитывают цепь при постоянном приложенном напряжении U ;
· рассчитывают цепь (обычно комплексным методом) при синусоидальном приложенном напряжении с амплитудой U1m частоты и частотой w (k=1);
· повторяют расчёт при k = 2, 3, 4, …, учитывая, что индуктивные сопротивления увеличиваются с ростом частоты ( 

· переходят к мгновенным значениям и суммируют постоянную и синусоидальные составляющие тока (напряжения) в каждой ветви;
· определяют действующие значения токов и напряжений, а также мощности по формулам:
где Uk, Ik – действующие значения синусоидальных составляющих.
Чем больше гармоник взято для расчёта, тем выше точность полученных результатов. На рис. 9.1 приведен в качестве примера экспериментальный график тока в
цепи с последовательным соединением R, L, и C при двуполярном прямоугольном приложенном напряжении. На этот график наложены в том же масштабе два расчётных графика: один сделан с учётом только первой и третьей гармоник, а в другом учтены 5 гармоник – с первой по одиннадцатую.
В приложении приведена MathCAD-программа расчёта этих графиков с комментариями.
Экспериментальная часть
Задание
Рассчитать мгновенное и действующее значение тока и напряжения на конденсаторе, а также потребляемую цепью активную мощность при прямоугольном периодическом приложенном напряжении, построить график изменения тока на входе цепи, проверить результаты расчёта путём осциллографирования и непосредственных измерений.
Порядок выполнения работы
· Выбрать один из приведенных ниже вариантов параметров цепи (рис. 9.2) и выполнить расчёт согласно заданию, учитывая основную гармонику и одну – две высших. По результатам расчёта мгновенных значений на рис.9.3 построить графики, а действующие значения и мощность занести в табл. 9.1.
Варианты параметров элементов цепи и приложенного напряжения:
L = 10 мГн (RK=17 Ом), L = 40 мГн (RK=70 Ом), L = 100 мГн, (RK=170 Ом);
С = 0,22, 0,47 или 1 мкФ;
R = 47, 100, 150, или 220 Ом;
Um=8…10 B, f=0,5…1 кГц.
· Собрать цепь (рис.9.2) с принятыми в расчёте параметрами элементов, включить виртуальные приборы для измерения действующих значений тока и напряжения на конденсаторе и осциллограф.
· Установить на источнике принятые значение частоты и амплитуду прямоугольных импульсов и перенести осциллограмм на рис. 9.4. Записать в табл. 9.1 действующие значения тока и напряжения на конденсаторе.
· Переключить вольтметр на вход цепи, включить виртуальный измеритель активной мощности и занести его показание также в табл. 9.1.
· Сравнить результаты расчёта и эксперимента и сделать выводы.
Видео:Поведение нагрузки при обрыве фазы на стороне ВН (опыт 5)Скачать

Трехфазные цепи при соединении треугольником
Особенности включения трехфазных систем треугольником. При соединении трехфазных систем треугольником также используются три гармонических напряжения (4.1), которые были рассмотрены в лекции 15. Однако соединение этих источников выполняется таким образом, что начало одной фазы соединяется с концом другой. На рис. 4.5а показано такое включение трех обмоток генератора и соответствующее ему включение источников напряжения 
Векторная диаграмма для, соединения обмоток генератора по схеме треугольника приведена на рис. 4.5, б. На этой диаграмме полагается, что вектора напряжений генератора имеют значения

т. е. генератор считается симметричным с прямым чередованием фаз.
При соединении нагрузок треугольником фазные напряжения будут равны линейным, а линейные токи равны геометрической разности двух фазных токов, подходящих к вершине треугольника нагрузок, как показано на рис. 4.6. При этом для положительных направлений токов справедливы следующие соотношения, которые устанавливают связь между линейными и фазными токами

Фазные токи рассчитываются по известным линейным напряжениям 

Если падения напряжений на проводах линий передачи малы, то можно считать, что напряжения генератора равны соответствующим напряжениям приемника, т. е. 
Из уравнений (26.2) также следует, что при любых значениях фазных токов для линейных токов справедливо выражение
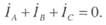
Следует отметить, что включение нагрузок по схеме треугольника возможно при любом включении обмоток генератора, как по схеме треугольника, так и по схеме звезды. Однако, при включении генератора по схеме звезды фазные напряжения приемника будут равны линейным напряжениям генератора. При этом нулевая точка генератора не используется.
Рассмотрим некоторые частные режимы работы при включении нагрузок по схеме треугольника. К таким режимам относятся:
□ равномерная нагрузка фаз генератора;
□ неравномерная нагрузка фаз генератора;
□ обрыв одной фазы приемника;
□ обрыв двух фаз приемника;
□ обрыв линейного провода.
Короткое замыкание любой фазы приемника приводит к аварийному режиму, так как при этом замыкается накоротко одна из обмоток генератора, и поэтому недопустимо.
Равномерная нагрузка фаз генератора.При симметричной системе напряжений генератора, определяемых уравнениями (4.1) и одинаковой нагрузке фаз приемника (YAB = YBC = YCA = Yn) действующие значения токов в фазах равны между собой, поэтому линейные токи связаны с фазными токами соотношением
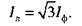
Токи в фазах приемника определяются по формулам (4.3) и при равенстве проводимостей имеют значения
Векторная диаграмма для равномерной нагрузки фаз генератора приведена на рис. 4.7а.
Неравномерная нагрузка фаз генератора.Неравномерная нагрузка фаз генератора является наиболее распространенным режимом работы трехфазной системы. Неравномерная нагрузка характеризуется различными значениями проводимостей, включенных в приемнике, т. е. YAB = YBC = YCA. Действующие значения токов в фазах приемника при неравномерной нагрузке и симметричном генераторе пропорциональны проводимостям нагрузки и определяются по формулам (26.3).
Векторная диаграмма для неравномерной нагрузки фаз генератора приведена на рис. 4.7б. Линейные токи при неравномерной нагрузке фаз можно определить по формулам (4.2).
Обрыв одной фазы приемника. При обрыве одной фазы приемника ток в ней будет равен нулю. Токи в других фазах приемника не изменятся, так как не изменятся фазные напряжения.
В линейном проводе, не связанном с оборванной фазой, ток также не изменится. Линейные токи двух других фаз станут равными фазным токам.
Например, при обрыве фазы А-В приемника ток IAВ = 0, а токи других фаз не изменятся. Линейные токи в этом случае будут иметь следующие значения

Векторная диаграмма обрыва фазы А-В приведена на рис. 4.7, в.
Обрыв двух фаз приемника. При обрыве двух фаз приемника ток в них будет равен нулю. Ток в неповрежденной фазе не изменится, так как напряжение на ней сохранится неизменным.
Ток в линейном проводе, подходящем к оборванным фазам, будет равен нулю. Токи в других линейных проводах станут равны фазным токам.
Так, например, при обрыве фаз А-В и В-С фазные токи IАВ = IBC = 0, а линейные токи примут значения

Векторная диаграмма токов и напряжений при обрыве двух фаз приемник приведена на рис. 4.7, г.
Обрыв линейного провода. При обрыве линейного провода трехфазная система превращается в однофазную. При этом напряжение и ток в фазе, не связанной с оборванным линейным проводом, останутся без изменений.
Две другие фазы, связанные с оборванным линейным проводом, оказываются соединенными последовательно и подключенными параллельно первой фазе.
Так, например, при обрыве линейного провода А фазы А-В и В-С будут включены последовательно и подключены параллельно фазе В-С, напряжение на которой равно UBC.
Токи в фазах определяются уравнениями
Векторная диаграмма токов и напряжений при обрыве линейного провода приведена на рис. 4.7, д.
Трехфазная система звезда — треугольник. Выше было сказано, что способ соединения обмоток генератора не предопределяет способ соединения нагрузок. Поэтому на практике к трехфазному генератору, включенному по схеме звезды, можно подключить нагрузку, соединенную по схеме треугольника. Схема подобного подключения приведена на рис. 4.8.
Из этой схемы следует, что каждое плечо треугольника оказывается включенным на линейное напряжение генератора; соединенного по схеме звезды. Поскольку линейное напряжение в 3 раза больше фазного, то токи в фазах симметричного приемника также вырастут в 3 раза. В общем случае их можно определить по формулам

При расчете от системы звезда-треугольник можно перейти к системе звезда-звезда. При таком преобразовании можно использовать эквивалентность схем звезды и треугольника, при которой сохраняются все напряжения и токи на внешних зажимах этих схем. Такое преобразование приводит в общем случае к эквивалентным сопротивлениям схемы звезды

Из уравнений (4.10) получим, что для симметричного треугольника с проводимостями YΔ можно найти сопротивления эквивалентной звезды
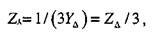
откуда следует, что сопротивления эквивалентной звезды для симметричной схемы в три раза меньше сопротивлений треугольника.
Следует отметить, что хотя в результате такого преобразования получается система звезда-звезда, ввести в нее нулевой провод нельзя, так как в реальной схеме этого соединения нет и при введении нулевого провода получается схема, отличная от исходной.
Пример 2. Требуется определить линейные токи в нагрузке, соединенной треугольником, которая подключена к симметричному трехфазному генератору с линейным напряжением Ел = 220 В. Сопротивления фаз приемника имеют значения: ZAB = ZBC = 50 Ом, ZCA = (30 + j40) Ом. Схема соединений генератора t нагрузкой приведена на рис. 4.9, а.
Решение. Приемник с такими нагрузками относится к разряду схем с неравномерной нагрузкой фаз генератора. Для определения линейных токов в такой схеме можно воспользоваться уравнениями (4.2), в которые входят фазные токи, определяемые по уравнениям (4.3). В связи с этим, определим вначале фазные токи, пользуясь уравнениями (4.3)
Далее с помощью формул (4.2) определим линейные токи
Сумма линейных токов в цепи
что подтверждает корректность решения. Векторная диаграмма токов и напряжений в схеме приведена на рис. 4.9б.
Видео:Несимметричная нагрузка. Схема соединения "треугольник"Скачать

3.5. Несимметричные и аварийные режимы работы трехфазных цепей
Для соединения трехфазной цепи в звезду возможны следующие аварийные режимы работы:
1) обрыв фазы (рис. 3.10);
2) обрыв нулевого провода (рис. 3.11);
3) короткое замыкание фазы при обрыве нуля (рис. 3.12).
4) обрыв фазы и нуля, рис. 3.12.
Для соединения трехфазной цепи в треугольник возможны следующие аварийные режимы:
2) обрыв линейного провода.
Аварийные режимы в нагрузках соединенных звездой
1) При обрыве фазы А 




2) Обрыв нулевого провода не всегда вызывает аварию в трехфазных цепях. Если нагрузка симметрична, то обрыв нулевого провода не изменит токов нагрузок, так как для симметричной нагрузки

Для несимметричных нагрузок 
Для того чтобы показать это, используем метод двух узлов:
Напряжение 
3) При коротком замыкании фазы А и обрыве нуля напряжение этой фазы равно нулю:
Нагрузка фазы В увеличится в 

Аналогично и в фазе С:



4) Обрыв фазы и нулевого провода дает:

В оставшихся фазах токи будут одинаковыми, а напряжения на них будут зависеть от сопротивлений нагрузок (рис. 3.16).
 Аварийные режимы в нагрузках соединенных треугольником
Аварийные режимы в нагрузках соединенных треугольником
1) Обрыв фазы.
Ключ к1 замкнут, ключ к2 разомкнут (рис. 3.17). В этом режиме ток в фазе 
2)
Обрыв линейного провода. Ключ к1 разомкнут и ключ к2 замкнут (рис. 3.19). Фаза нагрузки с 

📹 Видео
Соединение обмоток треугольникомСкачать

Этому не учат, а стоило бы. Чем отличается звезда от треугольника? #звезда #треугольник #двигательСкачать

Обрыв нулевого провода в трехфазной сети. К чему это приводит?Скачать

Соединение треугольникомСкачать

Трёхфазный переменный ток. Соединение "звезда" и "треугольник"Скачать

Соединение трехфазных цепей звездой и треугольникомСкачать

Что такое перекос фаз и неравномерное распределение нагрузкиСкачать
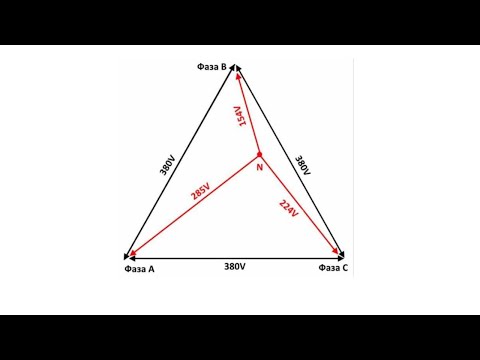
Трехфазные цепи. Схема соединения "ЗВЕЗДА"Скачать

#001."Звезда" или "Треугольник"?Скачать

КАК ТРИ ФАЗЫ "СЛИТЬ" В ОДНУ? Показываю ТРИ способа! #энерголикбезСкачать

Фаза на всех проводах. Индикатор показывает фазу. Наведенное напряжение. Наводка. Везде фаза.Скачать

Что будет, если перепутать начало и конец обмотки при включении трёхфазного электродвигателя.Скачать

Для чего нужен ноль? Почему у трехфазного двигателя нет нуля и куда девается ток?Скачать

Котика ударило током, 10 т. ВольтСкачать

Трехфазные электрические цепи │Теория ч. 1Скачать

Если в розетке 2 фазыСкачать

Что будет если ухудшится контакт в нулевом проводе или он отгорит? Перекос фаз и ток в нулеСкачать

Обрыв нуля. Откуда в розетке 380 ВольтСкачать





















 Аварийные режимы в нагрузках соединенных треугольником
Аварийные режимы в нагрузках соединенных треугольником