Обратная теорема равнобедренного треугольника доказательство

Теорема – это утверждение, справедливость которого устанавливается путем рассуждения. Само рассуждение называется доказательством теоремы.

Теорема обратная данной – это теорема, в которой условием является заключение данной теоремы, а заключением – ее условие. Например: Теорема: В равнобедренном треугольнике углы при основании равны. Обратная теорема: Если в треугольнике два угла равны, то он является равнобедренным.

Следствие – это утверждение, которое выводится непосредственно из теоремы. Например: следствием из теоремы о высоте равнобедренного треугольника является: Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.

Доказательство методом от противного заключается в следующем:

1) Делается предположение противоположное тому, что надо доказать.

2) Затем, исходя из предположения, путем рассуждений приходят к противоречию либо с условием, либо с известным фактом.

3) На основании полученного противоречия делается вывод о том, что предположение неверно, а значит верно то, что требовалось доказать.

Признак равенства прямоугольных треугольников по гипотенузе и катету.

Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

Дано:

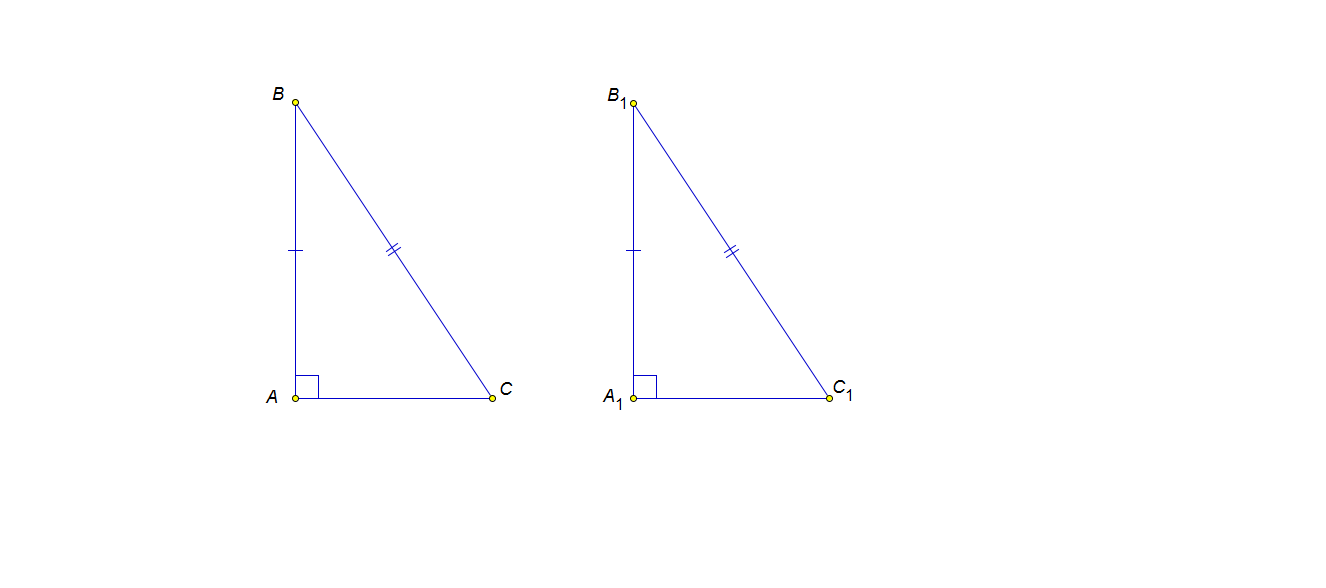
Доказать:

Доказательство:

1. Приложим к DАВС к DА₁В₁С₁, так чтобы вершина А совместилась с вершиной А₁, вершина В с вершиной В₁, а вершины С и С₁ оказались по разные стороны от прямой АВ.

2. Так как АВ= А₁В₁ Þ они совпадут.

3. ÐСА₁С₁= 90 0 + 90 0 = 180 0 ÞÐСА₁С₁ – развернутый и Þточки С, А₁ и С₁ – лежат на одной прямой.

4. Рассмотрим DСВС₁ – р/б (ВС= В₁С₁ по условию)Þ ÐС = ÐС₁ (по свойству)

5. Таким образом, DАВС = DА₁В₁С₁ – по гипотенузе и острому углу. (ч.т.д.)

Билет №9.

Перпендикулярные прямые. Перпендикуляр к прямой.

Перпендикулярные прямые – это две прямые, которые при пересечении образуют четыре прямых угла.(показать на рисунке)

Перпендикуляр к прямой – это отрезок, опущенный из точки на прямую под прямым углом. Точка пересечения отрезка и прямой называется основанием перпендикуляра (показать на рисунке)

1)Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой и притом только один.

2)Две прямые перпендикулярные к одной и той же прямой не пересекаются.

Признак равнобедренного треугольника.

Если в треугольнике два угла равны, то он является равнобедренным.

Дано:

Доказать:

Доказательство:

1. Мысленно скопируем DАВС и перевернем копию – получим DСВА.

2. Наложим DСВА на DАВС, так чтобы вершина С копии совместилась с вершиной А DАВС.

3. Так как ÐА = ÐС (по условию) Þ ÐА копии и ÐС треугольника при наложении совпадут, так же ÐС копии и ÐА треугольника при наложении совпадут.

4. Отрезок СВ копии наложится на луч АВ треугольника и отрезок АВ копии наложится на луч СВ треугольника.

5. Так как две прямые могут иметь только одну общую точку пересечения ⇒

т. В₁ совпадет с точкой В и ⇒ АВ совместится с СВ ⇒ АВ=СВ

6. Из того, что АВ=СВ ⇒ по определению ΔАВС — равнобедренный(ч.т.д.)

Билет №10.

Равнобедренный треугольник.

Треугольник, у которого две стороны равны, называется равнобедренным. Равные стороны называются боковыми сторонами, а третья сторона – основанием. (показать на рисунке)

Свойство равнобедренного треугольника: В равнобедренном треугольнике углы при основании равны.(показать на рисунке)

Признак равнобедренного треугольника: Если в треугольнике два угла равны, то он является равнобедренным. (показать на рисунке)

Теорема о высоте равнобедренного треугольника: Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой. (показать на рисунке)

Следствия из теоремы о высоте равнобедренного треугольника:

1) Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой. (показать на рисунке)

2) Биссектриса равнобедренного треугольника, проведенная к основанию, является высотой и медианой. (показать на рисунке)

Видео:Свойства равнобедренного треугольника. 7 класс.Скачать

Теорема о свойстве равнобедренного треугольника. Обратная теорема.

Видео:Геометрия 7 класс. Обратная теорема о равнобедренном треугольникеСкачать

Теорема о свойстве равнобедренного треугольника.

В равнобедренном треугольнике углы при основании равны. Доказательство. Пусть ABC — это наш равнобедренный треугольник с основанием AC. Этот треугольник отразим слева направо и получим новый треугольник C1BA1. Получившиеся два треугольника равны по двум сторонам и углу между ними. А в равных треугольниках против равных сторон лежат равные углы. Следовательно угол A равен углу C1, который по построению равен углу C. Значит углы A и C равны. ЧТД.

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Обратная теорема.

Обратная теорема если в треугольнике два угла равны, то треугольник равнобедренный. Доказательство: Пусть треугольник ABC — это наш треугольник с двумя равными углами A и C. Этот треугольник отразим слева направо и получим новый треугольник C1BA1. Получившиеся два треугольника равны по стороне и двум прилежащим к ней углам. А в равных треугольниках против равных углов лежат равные стороны. Значит сторона AB равна стороне C1B, которая по построению равна стороне CB. Это значит, что стороны AB и CB равны, то есть треугольник ABC — равнобедренный. ЧТД.

Видео:Геометрия. 7 класс. Теоремы. Т5. Первое свойство равнобедренного треугольника.Скачать

Второй и третий признаки равенства треугольников

Содержание

Как мы выяснили несколькими уроками ранее, определять равенство между треугольниками можно задействуя меньше данных о фигурах. Нам удалось познакомиться с одним подобным признаком — по равенству двух сторон и углу между ними. Теперь мы готовы разобрать еще два признака равенства, которые пригодятся вам в течение всего курса геометрии.

Видео:Что такое обратная и прямая теоремы. Примеры обратных и прямых теорем. Геометрия 7 класс.Скачать

Второй признак равенства треугольников

Второй признак равенства треугольников. Если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне и прилежащей к ней углам другого треугольника, то такие треугольники равны.

Пусть имеются треугольники $bigtriangleup$ и $bigtriangleup<A_B_C_>$, у которых равны стороны $AB$ и $A_B_1$ и углы при этих сторонах — $angle=angle,

angle=angle$. Докажем, что треугольники $bigtriangleup$ и $bigtriangleup<A_B_C_>$ равны.

Доказательство. Наложим треугольники друг на друга таким образом, что вершина $A$ совпадет с вершиной $A_1$, а вершины $C$ и $C_1$ будут находиться в одной полуплоскости от стороны $AB$. Поскольку $AB=A_B_1$, вершины $B$ и $B_1$ также совпадут при наложении.

Под вопросом остается расположение вершин $C$ и $C_1$ относительно друг друга. Поскольку $angle=angle,$ по аксиоме откладывания угла равного данному лучи $AC$ и $A_C_1$ будут совпадать. Аналогично совпадение лучей $BC$ и $B_C_$ по равенству углов $angle=angle$.

Раз лучи совпадают, точка пересечения лучей — вершина $C$, то вершина $C_1$ находится в той же точке, что и вершина $C$. Все три вершины совпадают, а значит треугольники $bigtriangleup$ и $bigtriangleup<A_B_C_>$ равны. Теорема доказана .

Запоминать полные формулировки теорем признаков равенства треугольников сложно и может вызвать путаницу. Это придет с опытом решения задач. Пока для вас, возможно, будет удобнее использовать фразу «признак равенства треугольников по…».

Например, второй признак равенства кратко можно перефразировать как «признак равенства треугольников по стороне и прилежащим к ней углам». А как бы вы перефразировали первый?

👍 Все просто: «Признак равенства треугольников по двум сторонам и углу между ними».

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Равнобедренный треугольник: обратная теорема

В точных науках существует понятие обратной теоремы: когда условие исходной теоремы используется в качестве заключения, а заключение — в качестве условия. Чтобы понять, как «работают» обратные теоремы, обратимся для примера к недавно нами доказанной теореме о равнобедренном треугольнике: «В равнобедренном треугольнике углы при основании равны».

— утверждение $A$ — это «равнобедренность треугольника»;
— утверждение $B$ — это «равенство углов при основании».

Логическая операция, к которой мы будем обращаться далее ($Rightarrow$), формально называется импликацией (от лат. ‘implicāre’, в переводе — «впутывать»).

Тогда с точки зрения логики мы можем сказать, что из утверждения $A$ следует утверждение $B$: если $A$, то $B$. Или на языке логики — $ARightarrow$. В обратной теореме утверждения меняются местами — $BRightarrow$, из $B$ следует $A$. В нашем случае читается обратная теорема так: «Если углы при основании равны, то треугольник равнобедренный».

Давайте проверим ее истинность.

Обратная теорема о равнобедренном треугольнике. Если два угла треугольника при основании равны, то такой треугольник является равнобедренным.

Доказательство

Из данного равенства следует, что $AC=BC$. Стороны при основании равны. Тогда $bigtriangleup$ равнобедренный. Теорема доказана.

Об импликациях

Несмотря на то, что прямое и обратное следствия для равнобедренных треугольников оказались истинными, мы не можем, к примеру, сказать то же про вертикальные углы. Действительно, если углы равны… то они вертикальны? Далеко не факт. Иными словами, истинность импликации не гарантирует истинность обратной импликации.

В быту же законы логики соблюдаются редко: мы все время перемешиваем меж собой заключения и условия и, что страшнее, превращаем корреляции в импликации. Например, всем давно известная корреляция между геймингом и детской жестокостью. Нужно понимать, что корреляция — это не более чем статистическая взаимосвязь случайных величин.

Скажем, автомобилист Гриша на третьем перекрестке по дороге домой всегда попадает на зеленый свет светофора. Имеем ли мы право перейти от случайной корреляции к фактическому следствию «если $A$, то $B$»? То есть сказать: «Если Гриша едет домой, то светофор всегда будет зеленым»?

К сожалению, люди размышляют именно так. Корреляция «часто жестокие дети играют в компьютерные игры» превращается в импликацию «если дети играют в игры, то они становятся жестокими».

Или еще хуже, в обратную импликацию: «если ребенок жестокий, то он играет в компьютерные игры».

Первое дает возможность родителям безапелляционно контролировать детей. Второе — снимать какую-либо ответственность за жестокое поведение ребенка с окружения. Импликация — мощное оружие. Особенно когда она используется вне законов науки логики. Так что в следующий раз, если услышите нечто подобное, можете смело заявить о некорректном переходе от корреляции к импликации.

Видео:Обратная теорема о равнобедренном треугольникеСкачать

Третий признак равенства треугольников

Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам второго треугольника, то такие треугольники равны.

Доказательство. Даны два треугольника $bigtriangleup$ и $bigtriangleup<A_B_C_1>$, в которых $AB=A_B_1,

BC=B_C_1$ и $CA=C_A_1$. Наложим треугольники друг на друга так, чтобы вершина $C_1$ располагалась в одной полуплоскости с вершиной $C$. Поскольку $AB=A_B_1,$ точка $A$ совпадет с точкой $A_1,$ точка $B$ совпадет с точкой $B_1$.

Воспользуемся методом доказательства от противного и предположим, что при наложении точка $C_1$ не лежит ни на луче $BC$, ни на луче $AC$. Тогда между вершинами $C$ и $C_1$ имеется расстояние $CC_1$. Обозначим точку $D$ как середину этого отрезка.

Рассмотрим треугольники $bigtriangleup<AC_C>$ и $bigtriangleup<BC_C>$.

Они являются равнобедренными, с общим основанием $CC_1$. В них $AD$ и $BD$ — медианы, поскольку $D$ мы обозначали как середину $CC_1$.

По теореме о медиане равнобедренного треугольника, медианы $AD$ и $BD$ также будут являться высотами соответствующих треугольников. Согласно теореме о единственности перпендикуляра, к точке прямой можно провести только один перпендикуляр. У нас — два перпендикуляра $AD$ и $BD$, к одной точке $D$.

Мы пришли к противоречию. Значит, точка $C_1$ располагается либо на луче $AC$, либо на луче $BC$. Если $C_1in,$ тогда $C_1$ совпадает с точкой $C$, поскольку $CA=C_A_1$. Точно так же приходим к выводу о совпадении точек $C$ и $C_1,$ если $C_1in$. Все три точки совпадают. Треугольники равны.

Теорема доказана .

Видео:Равнобедренный треугольник. Определение. Свойства. Теоремы и доказательства.Скачать

Задача

Попробуйте решить задачу самостоятельно. Ничего страшного, если где-то возникнет заминка: готовое решение находится ниже.

Треугольники $ABC$ и $ABC_1$ равнобедренные, с общим основанием $AB$. Докажите, что треугольники $ACC_1$ и $BCC_1$ равны.

🎦 Видео

Равнобедренный треугольник. 7 класс.Скачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Свойства равнобедренного треугольника. Практическая часть. 7 класс.Скачать

8 класс, 17 урок, Теорема, обратная теореме ПифагораСкачать

Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

✓ Свойства и признаки равнобедренного треугольника | Ботай со мной #008 | Борис ТрушинСкачать

Почему углы при основании равны в равнобедренном треугольникеСкачать

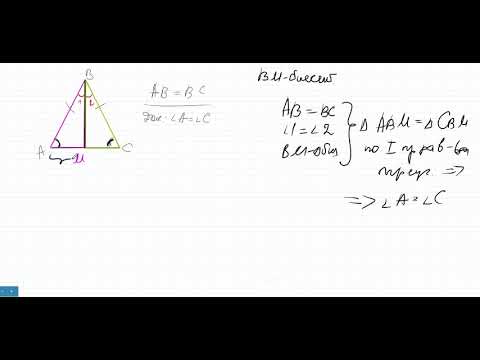
Признаки равнобедренного треугольника - геометрия 7 классСкачать

Равнобедренный треугольник. Практическая часть. 7 класс.Скачать

Задача, которую боятсяСкачать

Геометрия. 7 класс. Теоремы. Т6. Второе свойство равнобедренного треугольника.Скачать

7 класс. Геометрия. Урок 6. Свойства равнобедренного треугольника: теорияСкачать