Обозначьте на числовой окружности точки с абсциссой

Алгебра | 10 — 11 классы

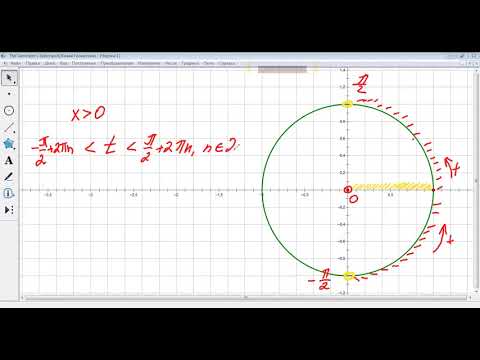
Обозначьте на числовой окружности точки с абциссой, удовлетворяющие неравенству х &gt ; — 1 / 2, и запишите при помощи двойного неравенства, каким числам t они соответствуют.

Решение смотрите во вложении.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Найдите на числовой окружности все точки с абсциссой или ординатой, удовлетворяющей заданному неравенству или системе неравенств, и запишите ( с помощью неравенства), каким числам t они соответствуют ?

Найдите на числовой окружности все точки с абсциссой или ординатой, удовлетворяющей заданному неравенству или системе неравенств, и запишите ( с помощью неравенства), каким числам t они соответствуют :

Видео:Точки на числовой окружностиСкачать

Обозначьте на числовой окружности точки t, удовлетворяющие уравнению sin t = √3 / 2, и запишите, каким числам t они соответствуют?

Обозначьте на числовой окружности точки t, удовлетворяющие уравнению sin t = √3 / 2, и запишите, каким числам t они соответствуют.

Видео:Координаты точек на числовой окружности. Алгебра 10 класс.Скачать

Найти на числовой окружности точки с абсциссой или ординатой, удовлетворяющие заданному неравенству, и записать с помощью двойного неравенства?

Найти на числовой окружности точки с абсциссой или ординатой, удовлетворяющие заданному неравенству, и записать с помощью двойного неравенства.

Видео:Как искать точки на тригонометрической окружности.Скачать

Решите неравенство : |3 — 2х|&gt ; = (больше или равно) 1?

Решите неравенство : |3 — 2х|&gt ; = (больше или равно) 1.

В ответ запишите наименьшее натуральное число, удовлетворяющее неравенству.

Видео:Определение значений по точкам на числовой окружностиСкачать

Найдите на числовой окружности точки с данной ординатой y = 0, 5, и запишите, каким числам t они соответствуют?

Найдите на числовой окружности точки с данной ординатой y = 0, 5, и запишите, каким числам t они соответствуют.

Видео:Математика 10 класс.Построение точек на числовой окружности 10 классСкачать

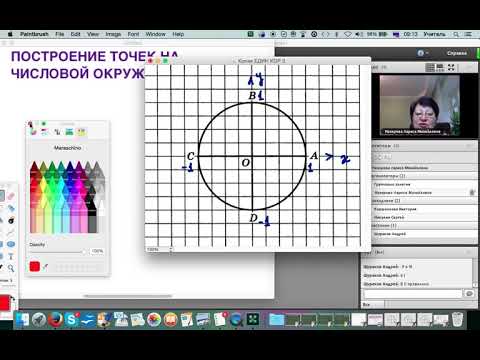
Как найти на числовой окружности точки?

Как найти на числовой окружности точки.

Которые соответствуют числам 4, 5 и — 3?

Какой четверти числовой окружности принадлежат точки, соответствующих числам 8, 4 , 3, и — 8?

Видео:Координаты точек на числовой окружности, часть 5. Алгебра 10 класс.Скачать

Найдите все целые числа удовлетворяющие двойному неравенству 1, 5 &lt ; | 2х — 1| &lt ; 5, 2?

Найдите все целые числа удовлетворяющие двойному неравенству 1, 5 &lt ; | 2х — 1| &lt ; 5, 2.

Видео:№ 5.10- Алгебра 10-11 класс МордковичСкачать

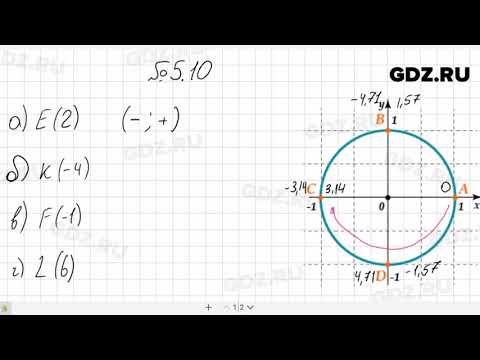
Найдите все числа, которым соответствуют отмеченные на числовой окружности точки?

Найдите все числа, которым соответствуют отмеченные на числовой окружности точки.

Видео:Координаты точек на числовой окружности, часть 3. Алгебра 10 класс.Скачать

ПОМОГИТЕ ?

СКОЛЬКО СМОЖИТЕ ХОТЯ БЫ укажите знаки абциссы и ординаты точки числовой окружности найдите на числовой окружности точки с абцисой или ординатой удовлетворяющей заданному неравенству и запишите с помощью двойного неравенства какими числами t они соответствуют 1.

Х меньше 1 / 2 3.

Х меньше√ 2 / 2 4.

Больше минус √2 / 2 5.

Видео:Соответствие чисел точкам числовой окружностиСкачать

Укажи какому числу t соответствует точка на числовой окружности, если её ордината удовлетворяет данному неравенству :у>0__πn 0

__πn 24 янв. 2022 г., 08:27:11

X — скорость автобуса 540 / (x + 30) = 540 / x — 3 x ^ 2 + 30x — 5400 = 0 теорема виетта сумма корней — 30 произведение — 5400 x = 60 ; — 90 скорость автобуса 60 , автомобиля 90.

Видео:10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать

Как обозначать числа с пи на числовой окружности?

Надеюсь, вы уже прочитали про числовую окружность и знаете, почему она называется числовой, где на ней начало координат и в какой стороне положительное направление. Если нет, то бегом читать ! Если вы, конечно, собираетесь находить точки на числовой окружности.

Видео:№ 4.6- Алгебра 10-11 класс МордковичСкачать

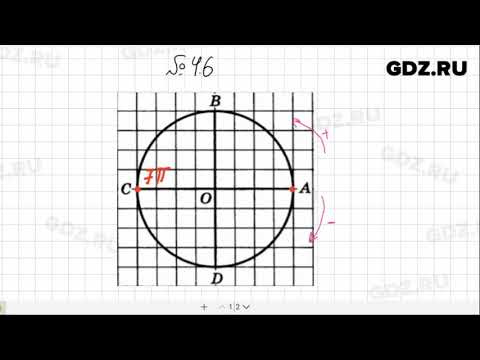
Обозначаем числа (2π), (π), (frac), (-frac), (frac)

Как вы знаете из прошлой статьи, радиус числовой окружности равен (1). Значит, длина окружности равняется (2π) (вычислили по формуле (l=2πR)). С учетом этого отметим (2π) на числовой окружности. Чтобы отметить это число нужно пройти от (0) по числовой окружности расстояние равно (2π) в положительном направлении, а так как длина окружности (2π), то получается, что мы сделаем полный оборот. То есть, числу (2π) и (0) соответствует одна и та же точка. Не переживайте, несколько значений для одной точки — это нормально для числовой окружности.

Теперь обозначим на числовой окружности число (π). (π) – это половина от (2π). Таким образом, чтобы отметить это число и соответствующую ему точку, нужно пройти от (0) в положительном направлении половину окружности.

Отметим точку (frac) . (frac) – это половина от (π), следовательно чтобы отметить это число, нужно от (0) пройти в положительном направлении расстояние равное половине (π), то есть четверть окружности.

Обозначим на окружности точки (-) (frac) . Двигаемся на такое же расстояние, как в прошлый раз, но в отрицательном направлении.

Нанесем (-π). Для этого пройдем расстояние равное половине окружности в отрицательном направлении.

Теперь рассмотрим пример посложнее. Отметим на окружности число (frac) . Для этого дробь (frac) переведем в смешанный вид (frac) (=1) (frac) , т.е. (frac) (=π+) (frac) . Значит, нужно от (0) в положительную сторону пройти расстояние в пол окружности и еще в четверть.

Задание 1. Отметьте на числовой окружности точки (-2π),(-) (frac) .

Видео:№ 4.11- Алгебра 10-11 класс МордковичСкачать

Обозначаем числа (frac), (frac), (frac)

Выше мы нашли значения в точках пересечения числовой окружности с осями (x) и (y). Теперь определим положение промежуточных точек. Для начала нанесем точки (frac) , (frac) и (frac) .
(frac) – это половина от (frac) (то есть, (frac) (=) (frac) (:2)) , поэтому расстояние (frac) – это половина четверти окружности.

(frac) – это треть от (π) (иначе говоря, (frac) (=π:3)), поэтому расстояние (frac) – это треть от полукруга.

(frac) – это половина (frac) (ведь (frac) (=) (frac) (:2)) поэтому расстояние (frac) – это половина от расстояния (frac) .

Вот так они расположены друг относительно друга:

Замечание: Расположение точек со значением (0), (frac) ,(π), (frac) , (frac) , (frac) , (frac) лучше просто запомнить. Без них числовая окружность, как компьютер без монитора, вроде бы и полезная штука, а использовать крайне неудобно.

Разные расстояние на окружности наглядно:

Видео:10 класс. Числовая окружность на координатной плоскости.Скачать

Обозначаем числа (frac), (-frac), (frac)

Обозначим на окружности точку (frac) , для этого выполним следующие преобразования: (frac) (=) (frac) (=) (frac) (+) (frac) (=π+) (frac) . Отсюда видно, что от нуля в положительную сторону надо пройти расстояние (π), а потом еще (frac) .

Отметим на окружности точку (-) (frac) . Преобразовываем: (-) (frac) (=-) (frac) (-) (frac) (=-π-) (frac) . Значит надо от (0) пройти в отрицательную сторону расстояние (π) и еще (frac) .

Нанесем точку (frac) , для этого преобразуем (frac) (=) (frac) (=) (frac) (-) (frac) (=2π-) (frac) . Значит, чтобы поставить точку со значением (frac) , надо от точки со значением (2π) пройти в отрицательную сторону расстояние (frac) .

Видео:Длина дуги числовой окружности | Алгебра 10 класс #9 | ИнфоурокСкачать

Обозначаем числа (10π), (-3π), (frac) ,(frac), (-frac), (-frac)

Запишем (10π) в виде (5 cdot 2π). Вспоминаем, что (2π) – это расстояние равное длине окружности, поэтому чтобы отметить точку (10π), нужно от нуля пройти расстояние равное (5) окружностям. Нетрудно догадаться, что мы окажемся снова в точке (0), просто сделаем пять оборотов.

Из этого примера можно сделать вывод:

Числам с разницей в (2πn), где (n∈Z) (то есть (n) — любое целое число) соответствует одна и та же точка.

То есть, чтобы поставить число со значением больше (2π) (или меньше (-2π)), надо выделить из него целое четное количество (π) ((2π), (8π), (-10π)…) и отбросить. Тем самым мы уберем из числа, не влияющие на положение точки «пустые обороты».

Точке, которой соответствует (0), также соответствуют все четные количества (π) ((±2π),(±4π),(±6π)…).

Теперь нанесем на окружность (-3π). (-3π=-π-2π), значит (-3π) и (–π) находятся в одном месте на окружности (так как отличаются на «пустой оборот» в (-2π)).

Кстати, там же будут находиться все нечетные (π).

Точке, которой соответствует (π), также соответствуют все нечетные количества (π) ((±π),(±3π),(±5π)…).

Сейчас обозначим число (frac) . Как обычно, преобразовываем: (frac) (=) (frac) (+) (frac) (=3π+) (frac) (=2π+π+) (frac) . Два пи – отбрасываем, и получается что, для обозначения числа (frac) нужно от нуля в положительную сторону пройти расстояние равное (π+) (frac) (т.е. половину окружности и еще четверть).

Отметим (frac) . Вновь преобразования: (frac) (=) (frac) (=) (frac) (+) (frac) (=5π+) (frac) (=4π+π+) (frac) . Ясно, что от нуля надо пройти расстояние равное (π+) (frac) – и мы найдем место точки (frac) .

Нанесем на окружность число (-) (frac) .
(-) (frac) (= -) (frac) (-) (frac) (=-10π-) (frac) . Значит, место (-) (frac) совпадает с местом числа (-) (frac) .

Обозначим (-) (frac) .
(-) (frac) (=-) (frac) (+) (frac) (=-5π+) (frac) (=-4π-π+) (frac) . Для обозначение (-) (frac) , на числовой окружности надо от точки со значением (–π) пройти в положительную сторону (frac) .

📹 Видео

Числовая окружностьСкачать

Координаты точек на числовой окружности, часть 2. Алгебра 10 класс.Скачать

Косинус на числовой окружности. Алгебра 10 класс.Скачать

Числовая окружность на координатной плоскости | Алгебра 10 класс #10 | ИнфоурокСкачать