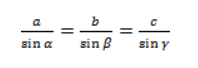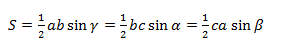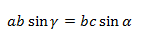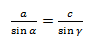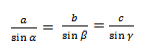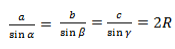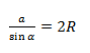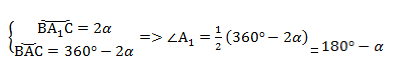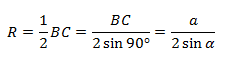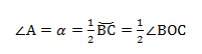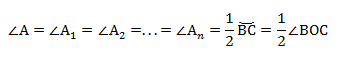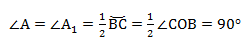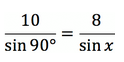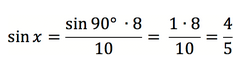Обобщенная теорема синусов для треугольника (6 видео)

Теорема синусов

Содержание

Решение задачи
Обобщенная теорема синусов
Доказательство теоремы синусов по учебнику Погорелова:
Серединный перпендикуляр к отрезку
Окружность, вписанная в треугольник
Теорема синусов: формулировка
Доказательство второй части теоремы синусов:
Доказательство обычной теоремы синусов
Теорема Виета.
Биссектрисы треугольника
Окружность, описанная около треугольника
Теорема синусов: доказательство
Теорема синусов
Доказательство теоремы синусов
Доказательство следствия из теоремы синусов
Теорема о вписанном в окружность угле
Примеры решения задач
Запоминаем
Теорема синусов. Доказательство
Примеры и решения

Видео:Теорема синусов – просто и красиво // Vital MathСкачать

Решение задачи

Также можно доказать следующий факт. Отношение любой стороны треугольника к синусу противолежащего угла равно диаметр описанной около треугольника окружности.

Другими словами, для любого треугольника ABC, у которого сторона AB = c, сторона BC = a, сторона CA = b, имеют место следующие равенства: a/sin(A) =b/sin(B) = c/sin(C) = 2*R. Здесь R – радиус описанной около треугольника окружности.

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Обобщенная теорема синусов

Теорема синусов — это тригонометрическая теорема, которой мы будем часто пользоваться. К сожалению, она обычно появляется в учебниках в урезанной форме, и в этом виде она не приносит всей той пользы, которую могла бы дать обобщенная теорема. Поэтому мы позволим себе доказать теорему синусов в желательной для нас форме.Мы начинаем с треугольника ABC (обозначенного обычным способом) и описываем вокруг него окружность с центром в точке O и радиусом R, как показано на рисунках 1 и 2. Проведем диаметр CJ и хорду BJ. В обоих случаях ∠CBJ — прямой, так как он вписан в полукруг. Следовательно, на обоих рисунках

На рисунке 1 Ĵ = Â, поскольку углы J и A опираются на одну и ту же дугу окружности. На рисунке 2 Ĵ = 180° − Â, потому что противоположные углы вписанного четырехугольника являются дополнительными. Вспоминая, что

, получим, что в обоих случаях sin Ĵ = sin Â, следовательно, sin Â = a / 2R, т. е.

a sin ⁡ A ^ = 2 ⁢ R

Та же самая процедура, примененная к другим углам треугольника ABC дает

b sin ⁡ B ^ = 2 ⁢ R , c sin ⁡ C ^ = 2 ⁢ R

Объединяя результаты, мы можем сформулировать обобщенную теорему синусов следующим образом:

Теорема 1.11. Для треугольника ABC с радиусом описанного круга R выполнены соотношения:

a sin ⁡ A ^ = b sin ⁡ B ^ = c sin ⁡ C ^ = 2 ⁢ R

Видео:9 класс, 13 урок, Теорема синусовСкачать

Доказательство теоремы синусов по учебнику Погорелова:

Применим формулу площади треугольника для двух углов A и C:

После приравнивания правых частей и сокращения на получим тоже самое равенство , как и в доказательстве первым способом. Из него тем же путем получаем равенство дробей.

Видео:Подготовка к ОГЭ. Теорема синусов. Доказательство.Скачать

Серединный перпендикуляр к отрезку

Определение 1 . Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).

Теорема 1 . Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.

Доказательство . Рассмотрим произвольную точку D , лежащую на серединном перпендикуляре к отрезку AB (рис.2), и докажем, что треугольники ADC и BDC равны .

Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты AC и BC равны, а катет DC является общим. Из равенства треугольников ADC и BDC вытекает равенство отрезков AD и DB . Теорема 1 доказана.

Теорема 2 (Обратная к теореме 1) . Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.

Доказательство . Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка E находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точки E и A лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок EA пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой D .

Докажем, что отрезок AE длиннее отрезка EB . Действительно,

Таким образом, в случае, когда точки E и A лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.

Теперь рассмотрим случай, когда точки E и A лежат по одну сторону от серединного перпендикуляра (рис.4). Докажем, что отрезок EB длиннее отрезка AE . Действительно,

Полученное противоречие и завершает доказательство теоремы 2

Видео:Теорема синусов с доказательствомСкачать

Окружность, вписанная в треугольник

Окружность называется вписанной в треугольник, если она касается всех его сторон.

Центр вписанной окружности совпадает с точкой пересечения биссектрис ;
Радиус вписанной окружности равен:
r = S p r=frac

p — полупериметр треугольника;
Отрезки, проведенные из одной вершины к точкам касания с окружностью, равны. Их можно выразить как разность полупериметра и противоположной стороны:
C A 1 = C B 1 = p − c CA_1=CB_1=p-c

~~C A 1 = C B 1 = p − c .~~

~~Видео:Решение задачи с применением теоремы синусовСкачать~~

Теорема синусов: формулировка

Что же нам сообщает теорема синусов? Вероятнее всего, что-нибудь о синусах, не правда ли? Давай сформулируем.

~~(здесь – радиус описанной окружности).~~

Первый вопрос, который возникает при взгляде на эту формулу: «Но при чём же здесь вообще ?». Вот давай именно с него и начнём.

~~Видео:Геометрия 9 класс (Урок№15 - Теорема синусов.)Скачать~~

Доказательство второй части теоремы синусов:

Опишем около данного треугольника окружность и через В проведем ее диаметр BD. Так как углы D и C опираются на одну дугу, то они равны (следствие из теоремы о вписанных углах). Тогда Опишем около данного треугольника окружность и через В проведем ее диаметр BD. Так как углы D и C опираются на одну дугу, то они равны (следствие из теоремы о вписанных углах). Тогда . Применим в треугольнике ABD определение синуса угла D: Что и требовалось доказать.

Задачи на вторую часть теоремы синусов:
1) В окружность радиуса 15 вписана трапеция. Длины диагонали и высоты трапеции соответственно равны 20 и 6. Найти боковую сторону.
2) Радиус окружность, описанной около трапеции, равен 25, а косинус ее тупого угла равен -0,28 (минус. ). Диагональ трапеции образует с основанием угол . Найти высоту трапеции.
3) В окружность радиуса 10 вписана трапеция. Длины диагонали и средней линии трапеции соответственно равны 15 и 12. Найти длину боковой стороны трапеции.
4) Олимпиада в Финансовой академии 2009г. Хорды окружности пересекаются в точке Q. Известно, что а радиус окружности равен 4см. Найдите длину хорды PN. Олимпиада в Финансовой академии 2009г.
5) В треугольнике PST . Вокруг точки пересечения его биссектрис и вершин P и T описана окружность с радиусом 8см. Найдите радиус окружности, описанной около треугольника PST (авторская задача).

Детально разобрать теорему синусов и получить необходимую практику ее использования в задачах вам всегда поможет репетитор по математике . Ее плановое школьное изучение происходит в курсе геометрии 9 класса в теме решение треугольников (по всем программам). Если вам нужна подготовка к ЕГЭ по математике для сдачи экзамена не менее чем на 70 баллов — придется тренироваться в решении крепких планиметрических задач с номеров С4. В них теорему синусов часто применяют к вписанным треугольникам учитывая соотношение . Помните об этом!

~~Видео:ЛУЧШЕЕ ДОКАЗАТЕЛЬСТВО теоремы СинусовСкачать~~

Доказательство обычной теоремы синусов

Воспользуемся только определением высоты треугольника, опущенной на сторону b, и синуса для двух углов. Следовательно, , что и требовалось доказать. Повторив те же рассуждения для двух других сторон треугольника, получаем окончательный вариант обычной теоремы синусов.

~~Видео:Теоремы синусов и косинусов | Ботай со мной #029 | Борис ТрушинСкачать~~

Теорема Виета.

Формулы Виета — это формулы, которые выражают коэффициенты многочлена через его корни.Теорема Виета.
Видео:101. Теорема синусовСкачать
Биссектрисы треугольника
Видео:Теорема СинусовСкачать
Окружность, описанная около треугольника
Определение 2 . Окружностью, описанной около треугольника , называют окружность, проходящую через все три вершины треугольника (рис.5). В этом случае треугольник называют треугольником, вписанным в окружность, или вписанным треугольником .
Видео:Теорема синусов и теорема косинусов а также РЕШЕНИЕ ТРЕУГОЛЬНИКОВСкачать
Теорема синусов: доказательство
Тебе уже известно, что около каждого треугольника можно описать окружность. Мы это и сделаем. А потом проведём диаметр . Пусть этот диаметр пересекает окружность в точке . Давай рассмотрим . Что же это за треугольник?
Ну, конечно же, прямоугольный, ведь в угол опирается на диаметр (вспоминаем тему « Окружность. Вписанный угол »).
Но и кроме того, в равен в , потому что эти углы опираются на одну дугу (опять вспоминаем ту же тему …).
А теперь просто запишем выражение для синуса в прямоугольном .
Но ведь – диаметр , и .
Вспомним, что и получим .
Вот и всё! Провели одну линию, рассмотрели один прямоугольный треугольник – и доказательство готово.
Но как же быть с углами и ? – спросишь ты. Да, точно также. Давай рассмотрим .
Теперь проведём диаметр и соединим точки и . Как-то тут немного по-другому получается, ты заметил? , конечно, прямоугольный, так как опирается на диаметр . Но теперь , потому что четырехугольник – вписанный. (Надеюсь, ты ещё помнишь, что для угла у нас было .) В чём же дело? Ну, просто – тупой, поэтому и получилось такое различие. Но, к счастью, для теоремы синусов это различие не играет роли. Сейчас мы в этом убедимся. Итак, запишем выражение для синуса в прямоугольном .
Ну вот, мы рассмотрели и острый, и тупой угол. Если ты все ещё беспокоишься об угле , то проделай все те же действия самостоятельно и убедись, что все получается. Обрати внимание, что мы доказали «четверное равенство».
в такой последовательности:
А теперь внимание! Обсудим пользу этой теоремы.
Понимаешь, теорема синусов – единственный разумный способ для нахождения радиуса описанной окружности.
Почему я так говорю? А ты вспомни сам: ну где ещё в формулах участвует ?! Возможно, правда, ты знаком с формулой , то есть , но!
Давай – ка сравним:
Из теоремы синусов:
Из формулы площади: .
Чувствуешь разницу? В первой формуле нужно знать только одну сторону и один угол, а во второй формуле – все стороны, да ещё и площадь! Ну и какую формулу легче применить? А кроме того, открою тебе маленький секрет: формула как раз и доказывается именно с применением теоремы синусов. Чтобы убедиться в этом, читай темы « Площадь круга и его частей , Площадь треугольника и четырехугольника ». Итак, теорема синусов бывает полезна и для нахождения синуса какого – то угла, если известны две стороны и один угол, но в основном теорема синусов – главный инструмент для нахождения радиуса описанной окружности. Запомни это очень хорошо!
Видео:Теорема синусов и теорема косинусовСкачать
Теорема синусов
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:#233. Теоремы синусов и косинусов | Формулы радиусов окружностейСкачать
Доказательство теоремы синусов
Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.
Нарисуем стандартный треугольник и запишем теорему формулой:

Формула теоремы синусов:

Докажем теорему с помощью формулы площади треугольника через синус его угла.

Из этой формулы мы получаем два соотношения:

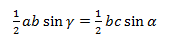
На b сокращаем, синусы переносим в знаменатели:

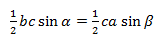
bc sinα = ca sinβ
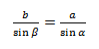
Из этих двух соотношений получаем:

Теорема синусов для треугольника доказана.
Эта теорема пригодится, чтобы найти:
Стороны треугольника, если даны два угла и одна сторона.
Углы треугольника, если даны две стороны и один прилежащий угол.
Видео:Как просто запомнить, что такое sin, cos, tg?! #косинус #синус #тангенс #математика #огэ #егэСкачать
Доказательство следствия из теоремы синусов
У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.

где R — радиус описанной около треугольника окружности.
Так образовались три формулы радиуса описанной окружности:

Основной смысл следствия из теоремы синусов заключен в этой формуле:

Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.
Для доказательства следствия теоремы синусов рассмотрим три случая.
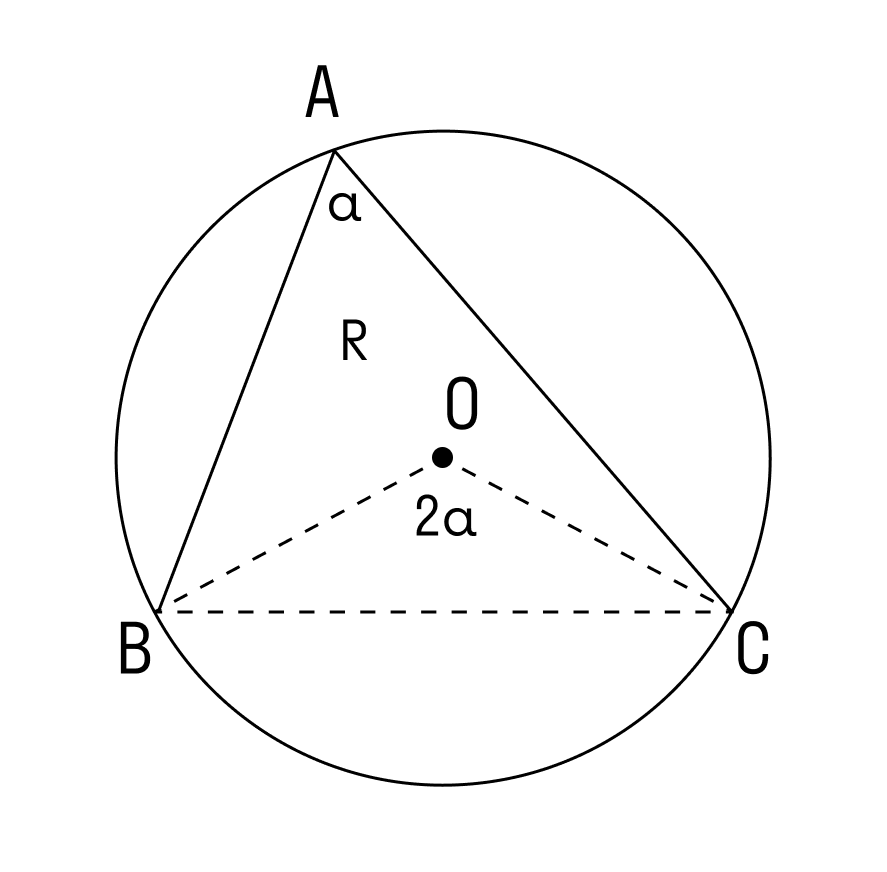
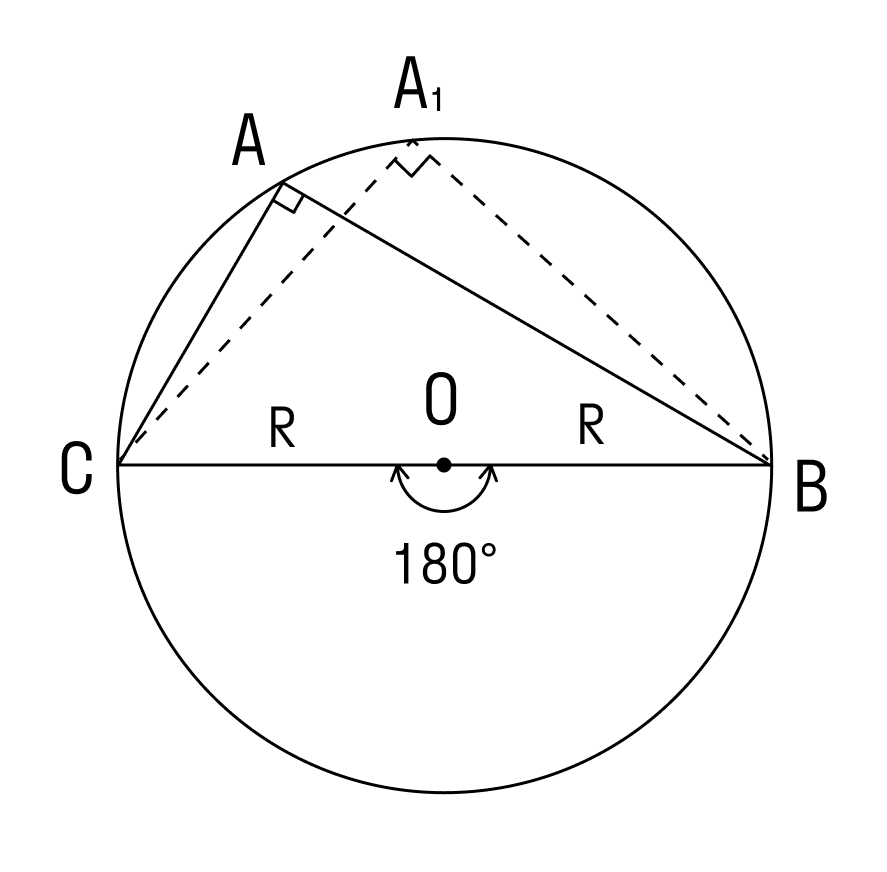
1. Угол ∠А = α — острый в треугольнике АВС.

Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.
Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.
Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.
BA1 = 2R, где R — радиус окружности
Следовательно: R = α/2 sinα
Для острого треугольника с описанной окружностью теорема доказана.
2. Угол ∠А = α — тупой в треугольнике АВС.
Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.
Следовательно, ∠А1 = 180° — α.

Вспомним свойство вписанного в окружность четырёхугольника:

Также известно, что sin(180° — α) = sinα.
В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:
α = 2R sin (180° — α) = 2R sinα
Следовательно: R = α/2 sinα
Для тупого треугольника с описанной окружностью теорема доказана.
Часто используемые тупые углы:
sin120° = sin(180° — 60°) = sin60° = 3/√2;
sin150° = sin(180° — 30°) = sin30° = 1/2;
sin135° = sin(180° — 45°) = sin45° = 2/√2.
3. Угол ∠А = 90°.

В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.

Для прямоугольного треугольника с описанной окружностью теорема доказана.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Видео:Теорема СинусовСкачать
Теорема о вписанном в окружность угле
Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.
Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.
Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.

∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.
Формула теоремы о вписанном угле:

Следствие 1 из теоремы о вписанном в окружность угле
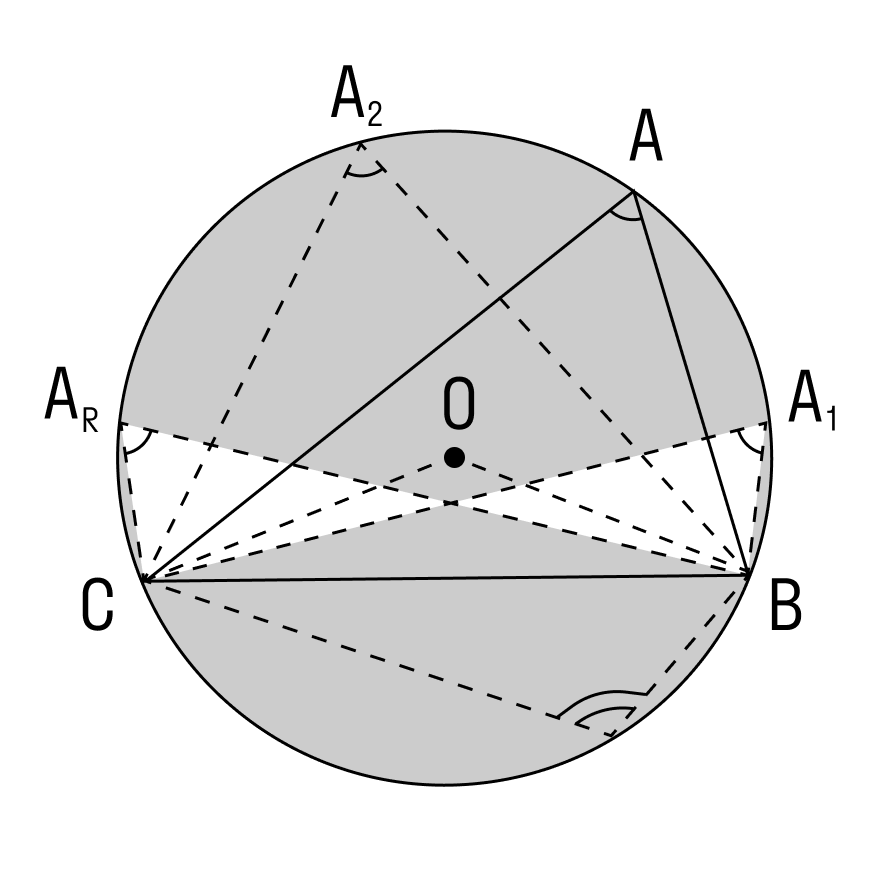
Вписанные углы, опирающиеся на одну дугу, равны.

∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).
Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:

На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.
Следствие 2 из теоремы о вписанном в окружность угле
Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.

ВС — диаметр описанной окружности, следовательно ∠COB = 180°.

Следствие 3 из теоремы о вписанном в окружность угле
Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:

Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.
Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.
Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.
Следовательно: α + γ = 180°.
Поэтому: ∠A + ∠C = 180°.
Следствие 4 из теоремы о вписанном в окружность угле
Синусы противоположных углов вписанного четырехугольника равны. То есть:
sinγ = sin(180° — α)
Так как sin(180° — α) = sinα, то sinγ = sin(180° — α) = sinα
Видео:9 класс. Геометрия. Теорема синусовСкачать
Примеры решения задач
Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.
Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.
Согласно теореме о сумме углов треугольника:
∠B = 180° — 45° — 15° = 120°
Сторону AC найдем по теореме синусов:
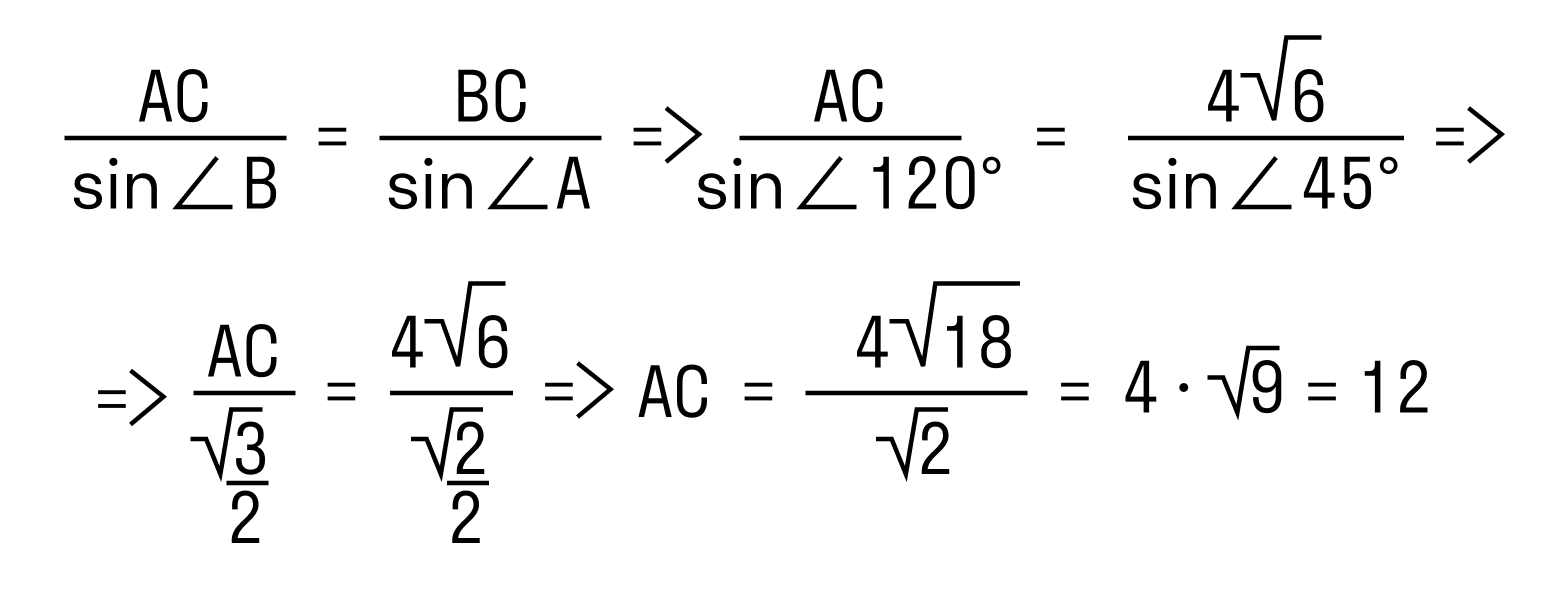
Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.
В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:

Значит x = sin (4/5) ≈ 53,1°.
Ответ: угол составляет примерно 53,1°.
Видео:Теорема синусов. 9 класс. Геометрия. Решение задачСкачать
Запоминаем
Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.
>
Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:
Видео:Теорема синусов | Геометрия 7-9 класс #96 | ИнфоурокСкачать
Теорема синусов. Доказательство
Теорема 1 (теорема синусов). Стороны треугольника пропорциональны синусам противолежащих углов:
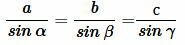. (a)
Доказательство. Пусть задан треугольник ABC. Проведем высоту h_b из вершины B на сторону b (Рис.1).
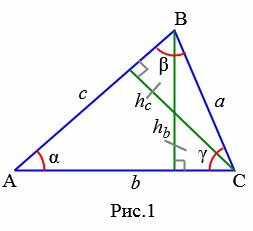Из определения синуса (см. страницу Синус и косинус. Онлайн калькулятор) следует, что синус угла α равен h_b если предполагать, что c=1. Но поскольку c может иметь любое значение, то имеем
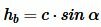Аналогично можем записать:
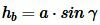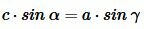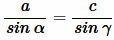(1)
Далее, для высоты h_c, опущенной из вершины C на сторону c, имеем:
, .
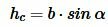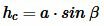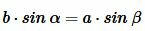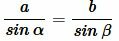. (2)
Из (1) и (2) получим:
.
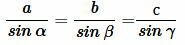Теорема 2 (расширенная теорема синусов). Для произвольного треугольника справедливо следующее равенство:
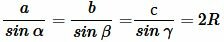, (b)
где a, b, c стороны треугольника, а α, β, γ противолежащие им углы, соответственно, R− радиус описанной около треугольника окружности.
Доказательство. Пусть задан треугольник ABC и описанная окружность с радиусом R, проходящей через вершины треугольника.
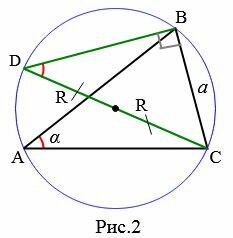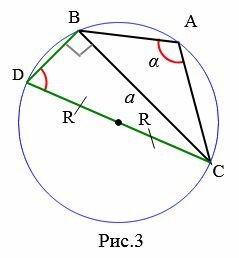
В теореме 1 мы доказали справедливость равенства (a). Для доказательства (b) достаточно показать, что
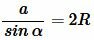. (3)
Проведем через вершину C диаметр CD описанной окружности и соединим точки D и B.
1. Пусть точки D и A лежат по одну сторону от BC (Рис.2). Полученный треугольник BCD являестся прямоугольным треугольником с прямым углом B, поскольку его одна сторона совпадает с диаметром окружности. А для этого прямоугольного треугольника справедливо равенство:
.
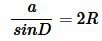Но 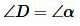поскольку обе эти углы опираются на дугу BC. Отсюда следует справедливость равенства (3).
2. Пусть точки D и A лежат в разные стороны от BC (Рис.3).
.
Поскольку BCD прямоугольный треугольник, то справедливо следующее равенство:
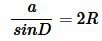. (4)
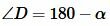
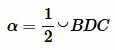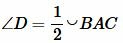Покажем, что . Действительно. Так как вписанный угол измеряется половиной дуги, на которой он упирается, то имеем:
, . (5)
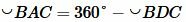. (6)
Тогда из (5) и (6) получим:
.
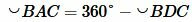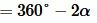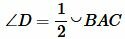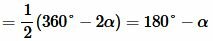. (7)
Учитывая (7), уравнение (4) можно записать так:
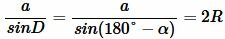. (8)
Но 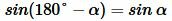. Тогда из (8) получим равенство (3).
Видео:ЗАДАЧА НА ТЕОРЕМУ КОСИНУСОВСкачать
Примеры и решения
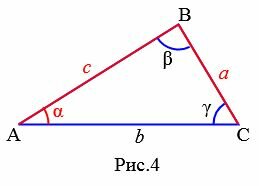
Задание 1. В треугольнике ABC a=8, c=10, угол α=30°. Найти сторону b (Рис.4).
Решение. Из теоремы синусов, имеем:
.
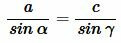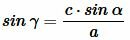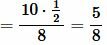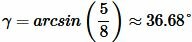Поскольку сумма всех углов треугольника равна 180°, то β=180°−30°−36.68°=113.32°.
Далее, из теоремы синусов:
,
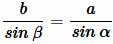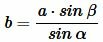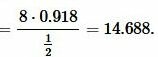Задание 2. В треугольнике ABC c=16, α=30°, β=45°. Найти стороны a, b (Рис.5).